
Радиотехнические системы
..pdf
161
ψ/ (t)= U (t)e j(ω0 +ωD )t ,
ψ/ (t −τ )= U (t −τ )e j(ω0 +ωD )(t−τ ) ,
Найдем, как и прежде, различие между сигналами
∞ |
ψ (t)-ψ / (t -τ ) |
2 |
|
é |
|
|
∞ |
ù |
ε 2 = ò |
|
dt = 4E |
- 2 Reêe j(2 |
πf0 |
+ωD )τ |
òU* (t)U (t -τ )e jωDt dtú. |
||
−∞ |
|
|
|
ë |
|
|
−∞ |
û |
Как и прежде высокочастотный сомножитель перед ин- тегралом опускаем ввиду практической невозможности его ис- пользования при узкополосных сигналах. Получим:
ε 2 = 4E − 2 Re(χ(τ , fD )),
где
∞ |
|
χ (τ , fD )= òU* (t)U(t −τ )e jωDt dt |
(6.7) |
−∞
- функция неопределённости по дальности и радиальной ско- рости.
По форме - это функция корреляции комплексной ампли- туды сигнала при наличии доплеровского сдвига частоты. На
основании свойств корреляционных функций она достигает максимума при нулевых значениях аргументов
χ(0,0) = χ(τ , fD ) | τ =0 = 2E..
fD =0
При этом ε 2 = 0.
Полагая, как частный случай, fD → 0, неопределенности по дальности:
∞
χ (τ ,0)= òU * (t)U (t − τ )dt = c(τ ).
−∞
получаем функцию
(6.8)
Полагая в другом частном случае τ → 0 , получаем
∞ |
|
χ(0, fD ) = k( fD ) = ò U (t) 2 e jωDt |
(6.9) |
−∞
- функция неопределённости по скорости (частоте) (преобразо- вание Фурье от квадрата модуля комплексной амплитуды).

162
Определим потенциальную разрешающую способность по частоте как основание прямоугольника, имеющего высоту
χ k(0D ) 2 и равновеликого с фигурой, образованной осью абс-
цисс и кривой |
|
k( fD ) |
|
2 |
(см. рисунок 6.4.) |
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
2 dfD |
|
||||||||||
|
|
δ f |
= |
ò |
|
k( fD ) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
−∞ |
|
|
|
|
|
|
. |
(6.10) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
DПот |
|
|
|
|
|
|
|
|
|
k(0) |
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно показать, что δ fD величина, |
обратная длительности |
|||||||||||||||||||||||||||
сигнала, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
δfD = |
1 |
|
|
, |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
τ Э |
|
|
|
|
|
|
|
|
||||||||||||||
где τЭ - эффективная длительность сигнала, |
|
|||||||||||||||||||||||||||
|
|
|
|
|
[ |
|
U ( fD ) |
|
2 dt]2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
τ Э = |
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ò |
|
U (t) |
|
4 dt |
|
|
|
|
|
|
|
(6.11) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рисунок 6.4. Квадрат модуля функции неопределенности по скорости
Функцию χ (τ , fD ) 2 - можно представить как поверхность
в трёхмерном пространстве. Эта поверхность называется по- верхностью неопределенности, а ограниченная ей фигура - те- лом неопределенности (см. рисунок 6.5).

163
Рисунок 6.5. Поверхность неопределенности для монохроматического
импульса с плавной огибающей
Количественно разрешающая способность по дальности и радиальной скорости оценивается как площадь внутри диаг- раммы неопределенности, которая находится как проекция на
плоскость τ, fD сечения поверхности неопределенности цилин-
дром, имеющим такой же объем и такую же высоту как тело неопределенности. Аналитически это записывается в виде:
δ (τ, f )= |
òò |
χ(τ, fD ) |
2 dτdfD |
(6.12) |
||
D |
|
|
χ(0,0) |
2 |
||
Фактически δ (τ , fD ) представляет собой площадь облас-
ти высокой корреляции (см. рисунок 6.6) и называется по Вуд- ворду эффективной площадью неопределенности.
fD |
Диаграмма неопределённости |
|
|
|
τ |
Обл. низкой корреляции Обл. высокой корреляции
Рисунок 6.6. Диаграмма неопределенности одиночного импульса

164
Если точка, τ, fD внутри диаграммы неопределенности,
то сигналы не разрешаются; если точка вне ее, то сигналы раз- решаются.
6.3. Принцип неопределённости в радиолокации
Независимо от формы сигнала δ (τ , fD )= 1!
Докажем это.
Используем формулу для эффективной площади неопре-
деленности. В ее знаменателе квадрат функции χ(0,0)= 2E. Сле- дует показать, что ее числитель
òò χ(τ , fD )2dτ ×dfD = 4E 2 .
Заменим квадрат модуля произведением комплексно со- пряженных функций и подставим в интеграл. Получим
χ(τ , fD )2 = χ(τ , fD )χ* (τ , fD ),
∞∞
òòòòU* (t1 )U (t1 -τ )×e jωDt1 ×U (t2 )U* (t2 -τ )×e− jωDt2 dt1dt2dfD dτ =
−∞−∞
∞
= ò òòòU* (t1 )U (t2 )U(t1 -τ )U* (t2 -τ )×e jωD (t1 −t2 )dt1dt2dτ dfD =
−∞
∞
= ò òòU* (t1 )U (t2 )U (t1 -τ )U* (t2 -τ )×δ (t1 - t2 )dt1dt2dτ
−∞
Далее, используя фильтрующее свойство d -функции, по- лучим:
∞
ò òU* (t1 )U (t1 )U (t1 −τ )U * (t1 −τ )dt1dτ =
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∞ |
|
|
|
|
∞ |
∞ |
||||||||||||
= ò ò |
|
U (t1 ) |
|
2 |
|
U (t1 −τ ) |
|
2 |
dt1dτ = ò |
|
U (t1 ) |
|
2 |
ò |
|
U (t1 −τ ) |
|
2 dτ dt1 = 4Е2 , |
|
|
|
|
|
|
|
|
|||||||||||
−∞ |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
−∞ |
|
|
|
|
что и требовалось доказать.

165
Принцип неопределенности означает, что нельзя изменяя параметры сигнала, одновременно улучшать разрешающую спо- собность по дальности и скорости. Одно можно делать за счет другого.
6.4. Функция неопределённости прямоугольного радиоимпульса
Рассмотрим простейший пример. Пусть сигнал - прямоу- гольный радиоимпульс с гармоническим заполнением (см. ри- сунок 6.7). Найдем его функцию неопределенности.
s(t)= A0 cos(ω0t); |
t ≤ |
τ И . |
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
s(t) |
|
|
− |
τ И |
|
|
|
τ И |
t |
|
2 |
|
|
|
2 |
|
|
U(t) |
А0 |
|
U(t - τ) |
||
|
|
|
τ |
|
|
t |
|
− |
τ И |
|
τ И |
|
|
|
|
2 |
|
|
2 |
|
Рисунок 6.7. К расчету функции неопределенности прямоугольного
радиоимпульса
Огибающая радиоимпульса (в данном случае действитель-
ная), U (t)= A0 ; t ≤ τ2И . Для вычисления функции неопреде-
ленности необходимо отдельно рассмотреть случаи положитель- ных и отрицательных временных сдвигов между импульсами. Пусть сначала τ > 0 , тогда ( см. рисунок 6.7).

166
|
τИ |
|
A02 |
|
|
|
0,5τИ |
χ(τ , fD ) = ò2 |
A02e jωDt dt = |
|
e j2π fDt |
|
|||
j2π |
|
|
-0,5τИ +τ . |
||||
− |
τИ |
+τ |
fD |
|
|||
|
|
||||||
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Подставляя пределы, находим далее квадрат модуля функ- ции неопределенности,
|
|
|
|
|
|
2 |
|
|
|
|
|
æ |
A2τ |
ö2 |
æ sin πfD (τ И -τ |
)ö2 |
|
|||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ç |
0 |
|
|
|
И |
÷ |
ç |
|
|
|
÷ |
|
|
|
|
χ(τ, fD ) |
|
= χ(τ, fD )χ |
|
|
(τ, fD )= 4ç |
2 |
÷ |
ç |
|
πfDτ И |
÷ |
, |
||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
è |
|
ø |
|
|||||||
откуда |
|
χ(τ, fD ) |
|
= 2E |
|
sin πfD (τ И |
-τ ) |
|
, |
τ ³ 0. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
πfDτ B |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
Расчет функции неопределенности для τ ≤ 0 , приводит к такой же формуле, с той лишь разницей, что в ней вместо τ стоит τ . Обобщая оба результата, запишем,
χ(τ, fD ) |
|
= 2E |
|
sin πfD (τ |
И |
- |
|
τ |
|
) |
|
. |
|
|
|
|
|
|
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
πfDτ B |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Для выяснения вида поверхности неопределенности, рас- смотрим ее сечения. Пусть сначала fD = 0. Переходя к соответ-
ствующему пределу, получим |
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
τ |
|
ö |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
ç |
- |
|
|
|
|
|
|
÷ |
|
τ |
|
£τ И . |
χ(τ,0)= c(τ )= 2Eç1 |
τ |
÷, |
|
|
||||||||
è |
|
И ø |
|
|
|
|
||||||
|
|
|
|
|
||||||||
Сечение тела неопределенности плоскостью fD = 0 при- ведено на рисунке 6.8.
χ (τ ,0)
2Е
τ
|
|
|
|
|
|
|
|
|
|
- τИ |
|
|
|
τИ |
|
τИ |
|
||
|
|
|||
|
|
Рисунок 6.8 |
|
|

167
Теперь найдем сечение тела неопределенности плоскостью τ = 0. После соответствующей подстановки получаем,
( ) ( ) sin πfDτ И χ 0, fD = k fD = 2E πfDτ И ,
Как и следовало ожидать, полученная формула соответ- ствует модулю спектра прямоугольного видеоимпульса, являю- щегося огибающей исходного сигнала. Его вид представлен на рисунке 6.9.
|
|
2E |
χ (0, fD ) |
|
|
|
fD |
− |
1 |
|
1 |
τ И |
|
τИ |
|
|
|
Рисунок 6.9 |
|
Приведенная на рисунке 6.10 диаграмма неопределенно- сти представляет собой сечение тела неопределенности гори-
зонтальной плоскостью на уровне 0,5χ(0,0).
Диаграмма неопределённости.
fD
Обл. высокой корреляции
1 |
|
τ |
||
τ |
|
|
|
|
Обл. низкой корреляции |
||||
|
|
|||
τ
Рисунок 6.10. Диаграмма неопределенности прямоугольного радиоим-
пульса
Чем больше длительность импульса, тем выше разрешаю- щая способность по частоте, но хуже разрешающая способность

168
по времени. Чем меньше длительность импульса, тем выше раз- решающая способность по времени, но хуже по частоте. Дан- ное положение является иллюстрацией принципа неопределен- ности в радиолокации.
6.5. Сложные сигналы. Функция неопределённости ФКМ сигнала
Выше показано, что объем тела неопределенности
χ(τ, fD ) 2 всегда равен 4E 2 .Отсюда следует, что идеальная фун-
кция неопределенности имеет вид перевернутой кнопки. Ее ос- новной объем должен быть сосредоточен в широком основа-
нии. За счет этого пик в точке τ = 0, fD = 0 должен быть узким
в обеих плоскостях, что обеспечивает хорошее разрешение по времени и частоте. Вид такой функции неопределенности пред- ставлен на рисунке 6.11.
τ |
fD
Рисунок 6.11. Идеальная функция неопределенности
Подобной функцией неопределенности обладает реали- зация белого шума, имеющая большую длительностьи одновре- менно бесконечно широкий спектр. Белый шум - математическая абстракция. На практике широкое применение нашли фазоко- доманипулированные (ФКМ) сигналы, функция корреляции ко- торых при удачном коде фазы приближается к идеальной. Прин- ципы построения ФКМ сигналов рассмотрены в подразделе 3.8.
169
ФКМ сигнал длительностью τИ состоит из N парциальных ра-
диоимпульсов, каждый из которых имеет свою начальную фазу. Совокупность начальных фаз образует код.
Самый лучший бинарный код фазы (начальные фазы пар- циальных радиоимпульсов нуль либо π ) - код Баркера. При его использовании уровень боковых лепестков функции неопреде- лённости по дальности равен 1/N.
Коды Баркера существуют для N = 3, 4,5,7,13 . Для N = 5
код имеет вид
0 |
0 |
0 |
1 |
0 |
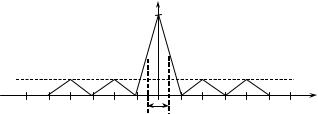
На рисунке 6.12 приводится функция корреляции соответ- ствующего сигнала.
χ(τ ,0)
1



 0,5
0,5
0,2 τ
τ1
Рисунок 6.12. Функция неопределенности по дальности ФКМ сигнала с кодом Баркера, N =5
С помощью согласованных фильтров производится сжа- тие сигналов во времени. Коэффициент сжатия равен базе сиг- нала,
kСЖ = Df ×τ И = b = N .
Действительно,
f = |
1 |
, |
b = f ×τ И = |
1 |
τ И = N . |
|
|
||||||
|
||||||
|
τ1 |
|
τ1 |
|||

170
Посколькукоды Баркера существуют только для N ≤ 13 коэф-
фициентсжатиядлямногихприложенийоказываетсянедостаточно большим. Поэтому применяют другие коды. Среди них наиболее употребительны М-последовательности (коды максимальной дли- ны). В этих кодах чередование нулей и единиц обладает свойства- ми случайной последовательности. Поэтому соответствующие сигналы называют шумоподобными. М-последовательности фор- мируют с помощью регистров сдвига (см. рисунок 6.13)
|
|
|
RG сдвига |
||||
такт. |
|
|
код |
||||
Т Т Т Т Т |
|||||||
|
|
||||||
|
|
|
|
|
|||
имп. |
|
||||||
|
|
|
|
||||
=1 |
Рисунок 6.13. Формирование M -последовательности
На вход регистра поступают тактовые импульсы с перио- дом τ1 и сдвигают содержащуюся в триггерах информацию на
один разряд вправо. В освободившийся крайний левый каскад
записывается результат суммирования по модулю два сигналов с некоторых триггерных ячеек.
Число триггерных ячеек n называется основанием кода. Наибольшее число, которое можно представить n-разрядным
двоичным кодом равно 2n . Длина M -последовательности (пе-
риод кода) равняется N = 2n −1: из 2n состояний регистра сдви- га исключается одно, когда во всех ячейках записаны нули, так
как суммирование нулей опять дает нуль и движение кода по регистру прекращается.
Полученный код используется для фазовой манипуляции, как показано на рисунке 6.14. Вид кода зависит от того, к каким ячейкам подключен сумматор по модулю два.
