
случая, соответствующего рис. 3.13, а, примет вид: |
|
x о.с(y) 0. |
(3.27) |
Соответственно линия переключения будет непрямой. Аналогичное искривление этой линии произойдет, если имеется нелинейность в канале основной обратной связи по x.
3.4. Фазовые портреты нелинейных систем
На рис. 3.14, а показаны фазовые траектории системы, неустойчивой в малом, но устойчивой в большом и имеющей устойчивый автоколебательный режим.
Незатухающим колебаниям соответствует замкнутая траектория, поскольку при этом переменные колеблются с постоянной амплитудой и, следовательно, изображающая точка бесконечно движется до одной и той же замкнутой траектории.
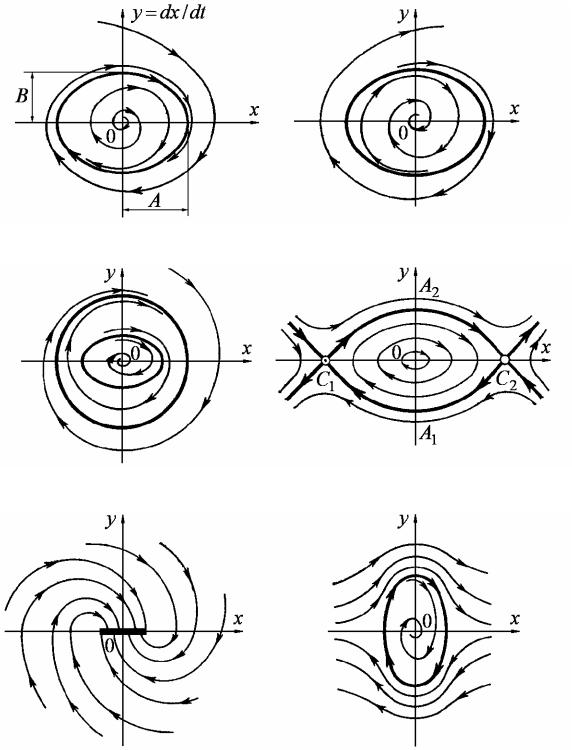
Замкнутые фазовые траектории называются предельными циклами. Они бывают устойчивыми и неустойчивыми. Устойчивый предельный цикл (рис. 3.14, а) соответствует автоколебаниям. Он характерен тем, что соседние фазовые траектории с обеих сторон от устойчивого предельного цикла наматываются на него. У неустойчивого предельного цикла (рис. 3.14, б) соседние фазовые траектории отходят с обеих сторон. Неустойчивый предельный цикл соответствует неустойчивым колебаниям, которые практически в системах не существуют, являясь промежуточным состоянием при переходе от одного установившегося режима к другому.
На рис. 3.14, в показан случай с двумя предельными циклами 1 и 2. Цикл 1 неустойчивый, а цикл 2 устойчивый. Этот случай отличается от рис. 3.14, а тем, что при больших отклонениях от установившегося режима возникают колебания, которые не расходятся бесконечно, а стягиваются к установившимся автоколебаниям.
74
а |
б |
в |
г |
д е
Рис. 3.14. Примеры фазовых портретов нелинейных систем
Системы с фазовым портретом, представленным на рис. 3.14, а,
называются системами с мягким режимом возбуждения колебаний.
В таких системах после их включения всегда устанавливаются автоколебания при любых начальных условиях и внешних
75
воздействиях.
Системы с фазовым портретом на рис. 3.14, в называются
системами с жестким режимом возбуждения колебаний. Для того чтобы в этих системах возникли автоколебания, соответствующие устойчивому циклу, необходимо создать достаточно большое начальное отклонение приложением, например, возмущения, при котором изображающая точка окажется вне устойчивого предельного цикла 1. Если после установления автоколебаний какое-либо возмущение сместит изображающую точку в сторону начала координат внутрь неустойчивого цикла 1, колебания в системе опять затухнут.
Заметим, что может быть также еще более удаленный устойчивый предельный цикл (рис. 3.14, е), соответствующий автоколебаниям с большой амплитудой. Такие же принципиальные качественные изменения картины фазовых траекторий при достаточно больших отклонениях могут наблюдаться и в случаях апериодических процессов, включая превращения их в колебательные и наоборот (рис. 3.14, е).
Аналогично для системы, находящейся согласно линейной теории на границе устойчивости (при чисто мнимых корнях), картина замкнутых фазовых траекторий может иметь место лишь вблизи состояния установившегося режима О. При больших отклонениях, если линейность характеристик звеньев системы нарушается, картина фазовых траекторий будет другой. Один из возможных вариантов изменения фазовых траекторий при больших отклонениях в этом случае показан на рис. 3.14, г. Здесь, кроме особой точки 0 типа центра, появляются два седла C1 и C2, что приводит фактически к неустойчивости системы. Но может иметь место и устойчивый предельный цикл. Особые линии такого типа, как C1A1C2 и C2A2C1 (рис. 3.14, г), на фазовой плоскости называются сепаратрисами.
При рассмотрении устойчивости нелинейных систем в дополнение к ранее введенным понятиям устойчивости в малом, в большом и в целом используется еще понятие асимптотической устойчивости. Асимптотическая устойчивость имеет место, если фазовые траектории вблизи начала координат асимптотически стягиваются к нему.
Примером неасимптотически устойчивой нелинейной системы является система с зоной нечувствительности и фазовым портретом,
76
показанным на рис. 3.14, д. Системы с фазовыми портретами на рис. 3.14, б, в и е асимптотически устойчивы в малом, т. е. при воздействиях, при которых изображающая точка не выходит за предельный неустойчивый цикл.
3.5. Метод точечных преобразований
Для получения более точных количественных оценок фазовых траекторий и, в частности, значений частоты и амплитуды возможных автоколебании А. А. Андроновым разработан метод точечных преобразований. Сущность его состоит в следующем.
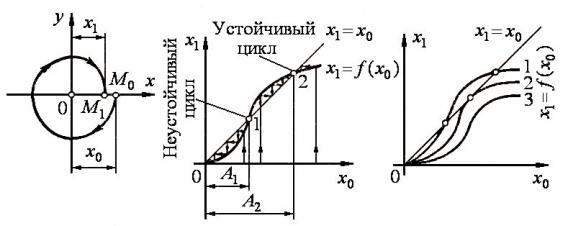
Возьмем начальное положение изображающей точки M0 в произвольном месте положительной полуоси x с абсциссой x0 (рис. 3.15, а). Обойдя один раз вокруг начала координат, изображающая точка окажется в некоторой другой точке M1 этой оси с абсциссой x1. Значение x1 может быть выражено как функция значения x0 через
уравнение |
фазовых траекторий. Возможный вид этой функции |
|
x1 f (x0) |
показан на рис. 3.15, б. По виду этой функции можно |
|
судить о характере поведения системы. Если |
x1 x0 (рис. 3.15, а), |
|
процесс является затухающим, а если x1 x0 |
– расходящимся. При |
|
x1 x0 имеет место предельный цикл (автоколебания).
Проведем на рис. 3.15, б биссектрису координатного угла, которая соответствует уравнению x1 x0. Тогда значения x0, соответствующие затухающим процессам, определятся участками зависимости f (x0), лежащими ниже биссектрисы (на рис. 3.15, б это участки левее точки 1 и правее точки 2), а расходящимся процессам будут соответствовать участки зависимости f (x0) выше биссектрисы (на рис. 3.15, б это участок между точками 1 и 2). Точка пересечения зависимости f (x0) с биссектрисой определяет амплитуду A, возможных автоколебаний в системе. При этом если кривая f (x0) пересекает биссектрису сверху вниз (точка 2 на рис. 3.15, б), колебания устойчивы, а если снизу вверх (точка 1 на рис. 3.15, б) – неустойчивы.
77
а |
б |
в |
Рис. 3.15. Метод точечных преобразований |
|
|
Для пояснения последнего утверждения на рис. 3.15, б тонкими линиями со стрелками показана последовательность изменения x во времени на разных участках зависимости f (x0). Здесь, начиная с произвольного исходного значения x0, вначале определяют соответствующее ему значение x1 путем проведения вертикальной линии с выбранной абсциссой x0 до пересечения с кривой f (x0). Далее, принимая это значение x1 за новое x0, определяют соответствующее ему новое значение х1. Для этого от первой точки кривой f (x0) проводят вначале горизонтальную линию до биссектрисы (перевод x1 в x0), а затем – вертикальную линию от нее до кривой f (x0). Из этой точки вновь проводят горизонтальную, затем вертикальную линии и т.д.
График на рис. 3.15, б соответствует устойчивости в малом системы, имеющей фазовый портрет, приведенный на рис. 3.14, в.
Определение x1 по x0, т. е. нахождение точки M1 по точке M0, называется точечным преобразованием. В результате обхода изображающей точкой начала координат точка M0 преобразуется в точку M1. Зависимость x1 f (x0) определяет такое точечное преобразование всех точек положительной полуоси x в соответствующие другие точки этой же полуоси, т. е. зависимость x1 f (x0) описывает точечное преобразование положительной полуоси x в саму себя, происходящее при обходе изображающей точкой начала координат. График x1 f (x0) называется диаграммой
78
точечного преобразования.
С помощью точечного преобразования, которое осуществляется по уравнению фазовых траекторий, можно, таким образом, исследовать характер возможных режимов в системе, не строя фазового портрета. Метод точечных преобразований удобен, в частности, для определения влияния изменения разных параметров системы на характер переходных процессов в ней. При этом могут быть определены критические, так называемые бифуркационные значения параметров, переход через которые качественно меняет фазовый портрет системы.
Для иллюстрации на рис. 3.15, в показано возможное изменение диаграммы точечного преобразования системы при вариации ее параметров. Кривая 1 повторяет диаграмму на рис. 3.15, б. Кривая 3 соответствует устойчивости в целом. Кривая 2 касается биссектрисы в точке, соответствующей полуустойчивому циклу. Эта кривая определяет бифуркационные значения параметров системы, при которых система находится на границе между качественно различными типами фазового портрета. При бесконечно малом отклонении параметров в одну сторону система становится устойчивой в целом (кривая 3 на рис. 3.15, в), а в другую – устойчивой только в малом с переходом к устойчивым автоколебаниям при больших отклонениях от установившегося режима (кривая 1 на рис. 3.15, в.)
Точечное преобразование можно осуществлять не обязательно для действительной полуоси x. Иногда, например, проще строить диаграмму точечного преобразования для полуоси y. В тех случаях, когда фазовый портрет симметричен относительно одной из координатных осей, как, например, на рис. 3.11, достаточно находить точечное преобразование для половины оборота изображающей точки вокруг начала координат, т. е. точечное преобразование положительной полуоси в отрицательную.
Если на фазовом портрете есть линии переключения, то обычно вместо координатных полуосей удобнее находить точечное преобразование для этих линий.
79
3.6.Контрольные вопросы
1.Что называют фазовым пространством и фазовым портретом системы управления?
2.Для систем какого порядка используется метод фазовой плоскости?
3.Перечислите виды корней характеристического уравнения.
4.Приведите классификацию предельных циклов. Чем они характерны?
5.Какие виды фазовых траекторий соответствуют апериодическим и колебательным переходным процессам?
6.Основные виды особых точек.
7.В чем различие систем с мягким режимом возбуждения колебаний и с жестким режимом возбуждения колебаний?
8.В чем заключается метод изоклин?
9.В чем заключается метод припасовывания фазовых траекторий?
10.В чем заключается метод точечных преобразований?
80
