2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 3 (1)

3.3. Исследование нелинейных систем на фазовой плоскости

Фазовый портрет дает полное представление о динамике нелинейной системы второго порядка при детерминированных воздействиях, включая точность, устойчивость и качество процессов. В связи с тем, что на фазовой плоскости в явном виде отсутствует время, из фазового портрета непосредственно нельзя определить только быстродействие системы. Однако приблизительную оценку его все же дать можно по величине скорости dx/dt выходной переменной, которая обычно используется в качестве второй координаты, откладываемой по оси ординат.

Действительно, в этом случае время перехода изображающей точки из одного положения в достаточно близкое последующее может быть приблизительно определено по формуле

t x ,

xср

где x – приращение x, соответствующее данному перемещению изображающей точки, а xср – среднее значение скорости dx/dt этого

перемещения, определяемое как ордината середины отрезка фазовой траектории между данными точками. Пользуясь этой формулой, можно по фазовой траектории приближенно построить соответствующую ей кривую переходного процесса x(t). В случае автоколебательного процесса можно таким же образом определить величину периода колебаний.

Фазовая плоскость является основным методом исследования нелинейных систем второго порядка. Это связано с тем, что для этих систем построение фазового портрета можно выполнить непосредственно по дифференциальному уравнению системы, не решая его.

Рассмотрим методику построения фазового портрета нелинейной системы второго порядка. В качестве координат примем отклонение x выходной величины системы от ее значения, соответствующего установившемуся режиму системы, и ее первую производную y dx/dt. Предварительно описание системы должно быть приведено к системе двух уравнений первого порядка следующего вида:

64

где y dx/dt, а Q и P – нелинейные функции от выходной величины

то, введя обозначение y dx/dt, из (3.8) непосредственно получим систему (3.13) в виде

Разделив первое уравнение (3.13) на второе, получим уравнение фазовых траекторий в виде нелинейного дифференциального уравнения первого порядка:

Таким образом, путем исключения времени мы упростили задачу, перейдя от уравнения второго порядка (или, что то же самое, от двух уравнений первого порядка) к одному уравнению первого порядка.

Метод изоклин. Однако построение траекторий в общем случае не требует решения и этого уравнения и может быть выполнено так называемым методом изоклин. Для этого вначале на фазовой плоскости строятся линии, соответствующие алгебраическому уравнению

называются изоклинами. Как следует из уравнения (3.16), для каждой

65

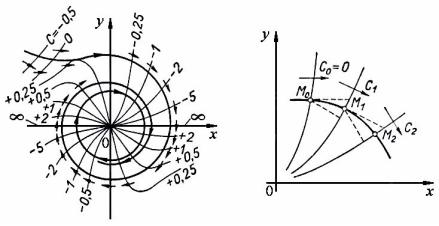
изоклины имеется равенство dy/dx C, т. е. изоклина – это геометрическое место точек с одинаковым наклоном фазовых траекторий, проходящих через эти точки. Величина C при этом определяет тангенс угла наклона фазовой траектории относительно оси абсцисс.

На рис. 3.9, а дан пример построения изоклин. Стрелочками на них показано направление фазовых траекторий. Здесь же цифрами обозначены соответствующие величины C.

По изоклинам нетрудно построить сами фазовые траектории, руководствуясь стрелочками. На рис. 3.9, б дается пояснение этой операции. Из произвольно выбранной начальной точки M0 проводятся два луча до пересечения со следующей изоклиной. Один луч имеет наклон, соответствующий стрелке на данной изоклине, а другой – стрелке на следующей изоклине. Точка M1 данной фазовой траектории на следующей изоклине определяется как середина отрезка между точками пересечения лучей с этой изоклиной. Таким же образом находится следующая точка M2 и т. д.

Метод припасовывания. Точность построения фазовой траектории может быть существенно повышена, если имеется возможность решить уравнение (3.15). В этом случае изоклины не строятся, а непосредственно путем интегрирования уравнения (3.15) находится зависимость между y и x, определяющая выражение для фазовых траекторий. В частности, такая возможность существует для широко распространенных нелинейностей, которые могут быть представлены кусочно-линейными характеристиками.

а б

Рис. 3.9. Построение фазовых траекторий с помощью изоклин

66

В случае таких кусочно-линейных характеристик нелинейных звеньев правая часть уравнения (3.15) системы представляет собой набор нескольких линейных функций, соответствующих отдельным линейным участкам характеристики нелинейного звена. В процессе изменения x и y происходит замена одной такой функции на другую в моменты прохождения через точки излома нелинейной характеристики. В результате фазовая характеристика разбивается соответственно на ряд участков, в пределах каждого из которых уравнение (3.15) является линейным и, следовательно, легко интегрируемым. Такой метод интегрирования по участкам уравнения с кусочно-линейной нелинейностью называется методом припасовывания (или сшивания).

На фазовой плоскости точкам излома кусочно-линейной характеристики соответствуют так называемые линии переключения. При пересечении фазовой траекторией этих линий происходит излом траекторий вследствие изменения правой части описывающего их уравнения (3.15).

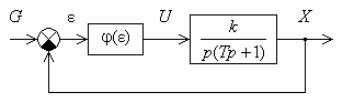
Пример 3.1. Рассмотрим для примера фазовый портрет нелинейной системы, структурная схема которой приведена на рис. 3.10. Здесь ( ) – кусочно-линейная статическая характеристика. В качестве этой характеристики возьмем некоторые релейные характеристики. Такую структурную схему может иметь, например, релейная следящая система. В этом случае X – это угол поворота: вала исполнительного двигателя, G – подлежащее отработке заданное значение X , а T – постоянная времени двигателя.

Рис. 3.10. Структурная схема нелинейной САУ

Решение. Изображенная на рис. 3.10 схема описывается следующей системой уравнений:

67

Ограничим свое рассмотрение поведением системы при отклонениях от установившегося режима, соответствующего постоянному значению задающего сигнала G. В этом случае, введя обозначения x X G и y px, будем иметь систему уравнений:

Разделив первое уравнение на второе и исключив таким образом время, получим дифференциальное уравнение фазовых траекторий:

уравнение (3.20) является линейным и поэтому легко интегрируется. Его решение имеет вид:

где C1 T[y0 k c ln(y k c)] x0; x0, y0 – начальные значения x и

Таким образом, фазовые траектории рассматриваемой системы описываются тремя друг друга сменяющими до ходу изображающей точки линейными уравнениями. Моменты перехода от одного уравнения к другому, т. е. моменты изменения величины с в уравнении (3.21), соответствуют переключениям реле и определяются его характеристикой. По ней легко строятся на фазовой плоскости линии переключения, представляющие собой геометрическое место

68

точек, в которых происходит переключение реле.

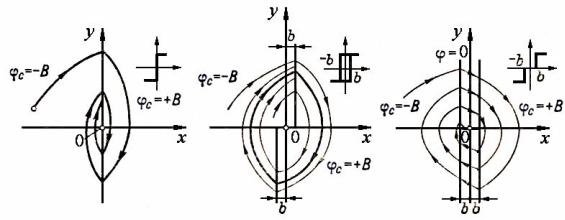
Рис. 3.11. Фазовые портреты нелинейных систем

На рис. 3.11 приведены построенные по уравнению (3.21) фазовые траектории рассматриваемой системы для трех вариантов релейных характеристик (x), изображенных здесь же. Жирными линиями показаны линии переключения. В первом случае (рис. 3.11, а) эта линия совпадает с осью ординат, поскольку ее уравнение, определяющее момент переключения реле, в соответствии с его характеристикой имеет вид:

x 0.

Во втором случае (рис. 3.11, б) уравнение линий переключения (их здесь две) будет

ав третьем случае (рис. 3.11, в) оно имеет вид:

xb.

Впоследнем случае отрезок оси абсцисс между этими линиями представляет собой особый отрезок, определяющий зону застоя системы из-за нечувствительности реле.

Справа от линий переключения фазовые траектории описываются уравнением (3.21) при с B, слева – при с B, а

между линиями переключения (в случае трехпозиционного реле – рис. 3.11, в) – при с 0.

Построение фазовой траектории, начатое в произвольно выбранной точке с координатами x0, y0, ведется по уравнению (3.21)

69

при соответствующем значении с вплоть до линии переключения. Здесь происходит изменение с, т. е. переход к другому уравнению. В качестве начальных значений x0 и y0 для этого очередного участка траектории берутся конечные значения переменных предыдущего участка. При следующем переходе через линию переключения вновь изменяется с и т. д.

Фазовый портрет на рис. 3.11, а соответствует устойчивой в целом системе. (Для такой двухпозиционной релейной системы в начале координат теоретически должны существовать автоколебания бесконечно малой амплитуды с бесконечно большой частотой.) На следующем фазовом портрете (рис. 3.11, б) имеется устойчивый предельный цикл и, следовательно, существует неустойчивость в малом. Физически последний факт очевиден. В данном случае двухпозиционное реле с зоной неоднозначности в отличие от такого же реле без этой зоны (рис. 3.11, а) не имеет состояния покоя при x 0. Установившийся режим системы с таким реле представляет собой автоколебания относительно, точки x 0. Система с фазовым портретом на рис. 3.11, в устойчива в целом, но неасимптотически изза наличия зоны нечувствительности у реле.

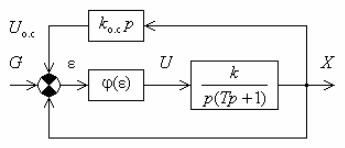
Пример 3.2. Чтобы продемонстрировать, как может изменяться фазовый портрет системы при изменении ее схемы, рассмотрим систему, структурная схема которой приведена на рис. 3.12. Эта система отличается от предыдущей введением корректирующей гибкой обратной связи (по скорости) через дифференцирующее звено с передаточной функцией kо.с p.

Рис. 3.12. Структурная схема нелинейной системы с гибкой обратной связью

Решение. Дифференциальное уравнение фазовых траекторий получается таким:

70

В связи с введением на входе реле дополнительного сигнала по производной в этом уравнении в отличие от уравнения (3.20) функция определяется не только x, но и ее производной y.

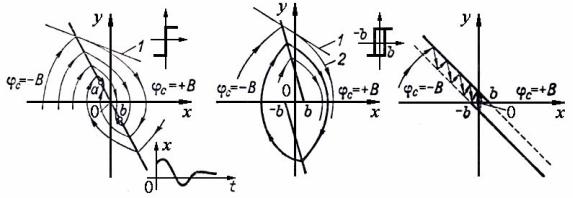
На рис. 3.13 показаны фазовые портреты данной системы при двух вариантах релейной характеристики.

Уравнение линии переключения на рис. 3.13, а

Введение дополнительного воздействия по скорости привело к наклону линий переключения, т. е. к зависимости значений x, при которых происходит переключение реле, от скорости изменения x. (Направление наклона линий переключения определяется при этом знаком сигнала по скорости, т. е. знаком обратной связи. Соответственно при положительной обратной связи линии повернутся в противоположную сторону.)

Рис. 3.13. Фазовые портреты системы, изображенной на рис. 3.12

Сравнение рис. 3.13, а и 3.11, а показывает, что введение воздействия по производной привело к принципиально новому типу

71

переходного процесса. Колебательность процесса уменьшилась, причем число колебаний стало конечным в связи с тем, что на линии переключения появился участок ab, к которому фазовые траектории подходят с обеих сторон, а отходящих траекторий нет. Изображающая точка, попав на этот участок, движется по нему в начало координат со скоростью, определяемой текущей координатой y. В соответствии с уравнением (3.25) линии переключения уравнение движения при этом будет

t

(3.26)

Таким образом, будучи вначале колебательным, переходный процесс заканчивается апериодическим хвостом. (См. внизу справа на рис. 3.13, а.)

Для пояснения причины появления участка ab на рис. 16.13, а показана касательная 1 к фазовой траектории в точке ее отхода от линии переключения. Чем ближе эта точка к началу координат, тем круче идет касательная. Когда ее наклон станет равным наклону линии переключения, изображающая точка пойдет по линии переключения, т. е. будет «скользить» по этой линии к началу координат.

Описанный режим, соответствующий участку ab, называется поэтому скользящим режимом. В этом режиме переходный процесс в релейной системе протекает, как в системе непрерывного действия [см. уравнение (3.26)].

При значениях x и y, соответствующих линии переключения, реле должно переключаться. Поэтому физически скользящий режим заключается в бесконечно быстрых переключениях реле, вызывающих соответственно колебания x с бесконечно малой амплитудой относительно постепенно спадающего к нулю среднего значения x. В реальных системах частота и амплитуда колебаний конечны, т. е. изображающая точка движется к началу координат, колеблясь относительно линии переключения. Поэтому в действительности хвост переходной характеристики на рис. 16.13, а представляет собой высокочастотные колебания, а изображенная на рисунке кривая является постоянной составляющей величины x.

Скользящий режим является одним из возможных способов осуществления так называемой вибрационной линеаризации. Природа этой линеаризации та же, что и у линеаризации нелинейных звеньев

72

случайным сигналом.

На рис. 3.13, б и в показаны фазовые портреты рассматриваемой системы с двухпозиционным реле, имеющим зону нечувствительности. При малом значении kо.с и соответственно малом наклоне линий переключения относительно оси ординат (рис. 3.13, б) фазовый портрет мало отличается от случая при kо.с 0 (рис. 3.11, б). Однако при достаточно сильной обратной связи в этой системе тоже возможен скользящий режим. Он показан на рис. 3.13, в. Как и в предыдущем случае, скользящий режим начинается в точке линии переключения, в которой наклон касательной (прямая 1 на рис. 16.13, б) к фазовой траектории (линия 2 на том же рисунке) становится больше наклона линии переключения. В результате фазовая траектория не пересекает линию переключения, а «отражается» от нее обратно, совершая колебания между двумя линиями переключения, соответствующими ширине петли статической характеристики реле. Показанные на рис. 3.13, в штрихами линии переключения относятся к «отраженным» от

3.13, б и 3.11, б эти линии не даны, так как там нет «отраженных» траекторий. Переходный процесс заканчивается установлением автоколебаний, амплитуда которых определяется шириной петли характеристики реле.

Таким образом, с ростом kо.с амплитуда устойчивых автоколебаний в системе уменьшается вплоть до величины, определяемой шириной петли характеристики реле.

Скользящий режим возможен и при трехпозиционном реле. В последнем случае изображенные на рис. 3.11, в линии переключения тоже наклоняются против часовой стрелки, а скользящий режим происходит путем движения изображающей точки по одной линии переключения до особой линии застоя на оси абсцисс. Это соответствует быстрым отключениям и включениям реле все время в одну и ту же сторону.

Линии переключения не обязательно являются прямыми линиями, как на рис. 3.11 и 3.13. Если, например, в системе, изображенной на рис. 3.12, измеритель скорости имеет нелинейную характеристику о.с(y), уравнение (3.24) линии переключения для

73