
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdfГ л а в а 11
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
ВПРОЗРАЧНЫХ СРЕДАХ
11.1.Распространение волн в сплошной среде. Показатель преломления
Предположим, что мы поставили задачу об электромагнитном поле в отсутствие источников, но не в вакууме, а в некоторой линейной среде, которую можно охарактеризовать константами <, 1. Конечно, безграничность такой среды еще более проблематична, нежели безграничность пустого пространства в предыдущей главе. Но как всегда в физических задачах, такую идеализацию следует понимать в смысле некоторого сильного неравенства. В данном случае условие применимости следует из ответа: характерный размер образца диэлектрика или характерный масштаб его неоднородности должен многократно превосходить длину волны.
Вместо (10.12) получаем систему уравнений:
<< |
11 |
0 |
; |
|
(11.1) |
0 |
|
|
|
|
Произошла, как мы видим, совершенно незначительная модификация — всего лишь в одном коэффициенте. Соответственно, и (10.13), (10.14) изменяются лишь в одном коэффициенте:
2 72 2 |
2 |
|
|
72 2 |
|
||||
|
|
|
; |
|
|
|
|
|
(11.2) |
2 0! |
|
0! |
|||||||
|
2 |
|
|||||||
Итак, мы опять пришли к волновому уравнению, и его решением снова будет монохроматическая плоская волна (10.15) при том же законе дисперсии (10.6), но скорость распространения волн будет меньше, чем в вакууме:
|
7 |
, где |
|
|
(11.3) |
|
<1 |
||||||
|
||||||
|
|
|
|
|
||
Величина называется коэффициентом преломления — как мы вскоре убедимся, она как раз соответствует коэффициенту преломления в оптике. Природа устроила так, что во всех без исключения средах, прозрачных в оптическом диапазоне, величина 1 с хорошей точностью равна единице, поэтому в оптике обычно без оговорок полагают <



11.3 ] |
Формулы Френеля |
357 |
в принципе для одной из вторичных волн — отраженной либо преломленной — ответ может включать знак « », что, конечно, должно получиться совершенно автоматически.
Введем амплитудные коэффициенты отражения и прозрачности следующим образом:
- 0 - 0; - 0 - 0 |
(11.11) |
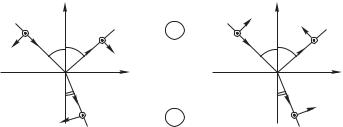
Мы ввели их через отношение амплитуд электрического поля в духе сделанного выше замечания о том, что при регистрации электромагнитных волн происходит измерение именно электрического поля. Если вычислительная процедура приведет к тому, что один из них окажется отрицательным, это будет означать просто фазовый сдвиг на $. В наших предположениях G <0 10 1 2-, при этом имеет смысл удерживать только фактор , все прочее можно будет в наших уравнениях сократить. Итак, для конкретной геометрии рис. 11.1 а (электрическое поле ортогонально плоскости падения) граничные условия (9.12), (9.15) преобразуются к виду
0 - - - ;
0 G G G B
- - - B
Эту систему уравнений с помощью введенных нами коэффициентов можно свести к следующей:
1 ; 1 B |
(11.12) |
F |
|
Как и было обещано, система уравнений переписана в универсальном виде, в ней фигурируют только функции углов падения и преломления. Решение (11.12) не представляет труда. Мы приводим сразу же ответ:
|
|
F |
; |
|
2 F |
|
(11.13) |
|
F |
|
|
F |
|
|
Здесь индекс означает поляризацию электрического вектора нормально к плоскости падения. Как мы и предвидели, высокая симметрия рис. 11.1 а не соблюдена — отражение происходит с потерей полуволны.
Надо заметить, что граничных условий в общей сложности четыре. Но условие (9.14) в данном случае вырождено, поскольку электрический вектор не имеет составляющей, нормальной к поверхности раздела. Обратимся к условию (9.13), которое для случая 1 1 может быть переписано для напряженности поля:0, или, что то же (см. рис. 11.1 а):
G G G B - - - B

358 Электромагнитные волны в прозрачных средах [ Гл. 11
Это условие тождественно удовлетворяется как следствие закона преломления и граничного условия на тангенциальные компоненты электрического поля. Тем самым мы убедились, что от-
вет (11.13) вполне корректен. |
|
|
Рассмотрим |
случай поляризации электрического |
векто- |
ра в плоскости |
падения (рис 11.1 б). Те же самые |
усло- |
вия (9.12), (9.15) теперь запишутся в виде
0 - - - B;
0 G G G - - -
F
В терминах коэффициентов отражения и прозрачности эта система уравнений может быть представлена следующим образом:
1 ; |
1 1 |
(11.14) |
|
F |
F |
F |
|
Решение (11.14), как и (11.12), сводится к стандартным тригонометрическим преобразованиям, хотя и несколько более громоздким. Ответ:
|
|
F |
; |
|
|
|
2 F |
|
(11.15) |
|
|
|
|||||||
|
F |
|
|
|
F F |
|
|
Предоставляем читателю самостоятельно убедиться в том, что граничное условие (9.14) в данном случае выполняется автоматически, а условие (9.13) вырождено.
Таким образом, задача решена полностью. Хорошей проверкой наших ответов будет сведение их к общему предельному случаю нормального падения, которому мы припишем коэффициенты 0, 0. Из рис. 11.1 следует, что значения коэффициента отражения, полученные предельным переходом из (11.13), (11.15), должны отличаться знаком — на рис. 11.1 а знак « » учитывает потерю полуволны, которая на рис. 11.1 б последует автоматически, потому что здесь сама амплитуда - — другого знака. С учетом этого обстоятельства искомые величины оказываются
равны следующим: |
|
|
|
|
|
|
|
0 |
|
1 |
; |
0 |
2 |
|
(11.16) |
|
1 |
1 |
|||||
|
|
|
|
|
|
Формулы (11.13), (11.15), (11.16) — именно они и называются формулами Френеля (по имени французского физика
О.Ж. Френеля (1788–1827)) — в достаточной мере универсальны с точки зрения соотношения коэффициентов преломления, т. е. они равным образом могут применяться при падении волны из вакуума на границу с диэлектриком, из диэлектрика в вакуум или на границу между двумя диэлектриками. При этом углы, B и коэффициенты преломления , , связаны законом (11.10).

11.4 ] |
Поляризационные эффекты. Поток энергии через границу |
359 |
11.4. Поляризационные эффекты. Поток энергии через границу
Сравнивая между собой коэффициенты отражения и прозрачности для различных поляризаций падающей волны — формулы (11.13) и (11.15), мы находим, что они отличаются друг от друга для всех углов падения, кроме нулевого — формула (11.16). Нам еще предстоит иметь дело с эффектом поляризации света в следующем разделе нашего курса, здесь же мы рассмотрим некоторые следствия такого рода из формул Френеля.
Дело в том, что естественный свет — и равным образом любые электромагнитные волны естественного происхождения — всегда неполяризованы. С точки зрения решений уравнений Максвелла это значит, что свет (излучение) представляет собой линейную смесь волн самых различных поляризаций. Мы уже обсуждали это свойство в связи с проблемой точечного источника. Разумеется, каждый отдельный квант, излучаемый возбужденным атомом, как-то поляризован, но если характерное время регистрации много больше времени замены одного такого кванта другим, с другой поляризацией, то мы этого не увидим. Это свойство присуще также и излучению искусственного происхождения, например, если его источник — тепловой природы: лампа накаливания, газоразрядная трубка (но не лазер!).
Теперь представим себе, что такое неполяризованное излучение падает, как это показано на рис. 11.1, на границу двух сред с разными . Ввиду различия коэффициентов (11.13) и (11.15), как отраженный, так и преломленный свет уже приобретет некоторую степень поляризации. Последнюю можно характеризовать, например, отношением средних квадратов электрического поля, соответствующего различным поляризациям. Неполяризованный свет (или иное электромагнитное излучение) отвечает условию
2 -2
-
Напомним, что в данном случае усреднение проводится по промежутку времени порядка или большему характерного времени регистрации. Для вторичных волн из (11.13) и (11.15) получаем
2 |
2 |
|
|
2 |
2 |
|
2 |
* |
# |
|
F |
; |
* |
|
2 B |
2 |
# |
|
F |
|
2 |
|
|
* |
|
|
|
|
* |
|
(11.17) |
|
|
|
|
|
|
|
Дадим для справки формальное определение степени поляризации электромагнитного излучения :
2 *2
*
2 *2
*
360 |
Электромагнитные волны в прозрачных средах |
[ Гл. 11 |
Особый интерес представляет возможность полной поляризации отраженного света при B $ 2 — уже из (11.15) видно, что при этом 0 Это означает, что в отраженном свете вектор E строго перпендикулярен плоскости падения. С учетом (11.10) находим соответствующий угол падения
B # |
(11.18) |
|
Этот угол называется углом Брюстера, что и отражено индексом. Заметим, что максимальная поляризация отраженного света не соответствует максимальной поляризации преломленного — это можно увидеть из второй формулы (11.17). Еще отметим следующее обстоятельство. Если диэлектрическая пластинка освещается белым светом, то условие (11.18) должно включать зависимость или, что то же, , и угол Брюстера будет разным для волн разной частоты.
Таким образом, простейший поляроид, доступный каждому, — это просто стеклянная пластинка, которую следует располагать так, чтобы свет падал на нее по возможности близко к B . С помощью такого поляроида нетрудно, например, заметить поляризацию света, отраженного от водной поверхности. Если же набрать пакет из таких пластинок и наблюдать источник света на просвет, то можно получить достаточно высокую степень поляризации, 4 B , где ! — число параллельных пластинок. (Фактор 4, вместо двойки, есть следствие того, что у каждой пластинки — две поверхности раздела сред.) Такой поля-
роид впервые был предложен русским физиком А. Г. Столетовым (1839–1896) и называется стопой Столетова.
Если и — амплитудные коэффициенты отражения и прозрачности, то 2 и 2 — то же для интенсивности. В этой связи обращает на себя внимание следующее обстоятельство. Вне зависимости от поляризации, из обеих формул (11.13) и (11.15) следует 2 2 1 Легче всего это увидеть из формул (11.16) для нормального падения, и в этом же случае легче всего прокомментировать. Никакого парадокса здесь нет, поскольку в задаче такого рода следует подводить баланс не энергии как таковой, а потока энергии.
Предположим, что электромагнитная волна падает из вакуума на границу диэлектрика. Падающий на границу поток энергии равен, согласно (11.8),
|
|
|
|
|
|
|
|
|
-2 , |
|
|
00 |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
!0 |
||||||||
|
|
|
|
|||||||
отраженный, соответственно, |
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
-2 , |
|||
|
|
00 |
|
|
||||||
|
||||||||||
|
0 |
|
||||||||
|
|
!0 |
|
|
|
|||||
