
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
10.4 ] Энергия и импульс электромагнитной волны 341
правую тройку (подобно координатной системе , , ), так что
координатную зависимость вместе с ориентацией полей в данный |
|||||
момент времени можно передать |
|
|
|||
рис. 10.1. |
|
|
|
E |
|
Сократим в (10.16) экспонен- |
|
||||
|
|
||||
|
|
||||
циальные осциллирующие мно- |
|
|
|||
жители, тогда это |
будут урав- |
|
|
||
B |
|||||
нения для амплитуд 0 и 0. |
|||||
|
|
||||
Подставим первое уравнение во |
|
|
|||
второе. Результат имеет вид |
|
k |
|||
|
2 |
|
|||
|
|
|
|||
! ! 0 ! ! 0 0 |
|
|
|||
10<0 |
2 |
(10.17) |
Рис. 10.1 |
||
0 |
|
|
|||
Первый член разности в (10.17) равен нулю в силу поперечности электромагнитной волны. Оставшиеся члены после сокращения 0 дают в ответе уже известный нам закон дисперсии
2 2 2
Выпадение из ответа амплитуды — в данном случае 0 — вообще характерное свойство т. н. линейной физики. Оно проистекает из самых основных законов, а именно, из того обстоятельства, что уравнения Максвелла (9.2)–(9.5) полностью сохраняют силу при умножении всех полей, токов и зарядов на один и тот же постоянный коэффициент. Поэтому, если токи и заряды связаны с полями линейной зависимостью или, как в данном случае, вовсе равны нулю, решение (10.15) можно умножать на любые коэффициенты, более того, любая линейная комбинация решений вида (10.15) с разными амплитудами и волновыми векторами (а тем самым, и частотами) также будет решением исходной системы уравнений. Это и есть «линейная физика». Только для этого предельного случая справедлив принцип суперпозиции полей, от которого приходится отказаться в случае нелинейности функций 3 , , , либо операторов <, 1 Нам уже знакомы такие примеры нелинейных сред, как сегнетоэлектрики и ферромагнетики; в этой связи заметим, что нелинейные проблемы в современной физике представляются скорее правилом, нежели исключением. Даже вакуум в квантовой электродинамике оказывается нелинейной средой.
10.4. Энергия и импульс электромагнитной волны
Плотность энергии в электромагнитной волне задается стандартным выражением (9.18)
= 12
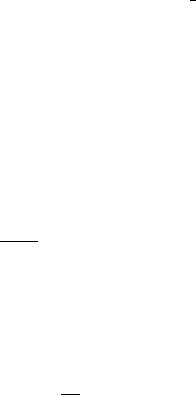
342 |
Электромагнитные волны |
[ Гл. 10 |
|
Это |
выражение квадратично по |
полю, поэтому |
подставлять |
в него непосредственно формулы |
(10.15) не следует — нужно |
||
воспользоваться их вещественным эквивалентом |
|
||
, 0 ! ; , 0 !
(10.18) (обратим еще раз внимание на синфазность электрического и магнитного полей). Плотность энергии волны будет, следовательно, осциллировать в пространстве и во времени. Обычно в таких случаях оперируют средним ее значением по периоду либо по длине волны. Эти величины равны друг другу. Действительно,
2 ! 1 2 ! ( 12
Таким образом, из (10.18) можно получить следующее значение плотности энергии в электромагнитной волне:
|
|
|
|
1 |
|
2 |
2 |
|
|
|
|
= |
|
|
|
0 |
|
(10.19) |
|||
|
|
<0-0 |
|
|||||||
4 |
!0 |
|||||||||
|
|
|
|
|
||||||
Воспользуемся первым из уравнений (10.16). Помимо ориентации основной тройки векторов, оно дает, с учетом поперечности волны, соотношение между амплитудами полей
0 -0
Подставим его в (10.19). Получаем две эквивалентных формы ответа:
|
|
|
2 |
2 |
|
|
2 |
|
|
||
= 00 |
-2 |
1 |
|
0 |
00!0 |
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|||
4 |
0 |
|
00!0 2 4!0 2 |
|
|
|
|||||
В силу закона дисперсии, дополнительное к единице слагаемое
вкаждой скобке также равно единице. Из этого следует, что средняя по периоду электрическая энергия равна средней магнитной, а поскольку поля синфазны, плотности электрической и магнитной энергии равны друг другу в любой момент времени
влюбой точке пространства. Окончательный ответ для усредненной плотности энергии мы по-прежнему приводим в двух
формах:
= 00 |
-2 1 |
2 |
(10.20) |
||
|
2 |
||||
0 2!0 |
0 |
|
|||
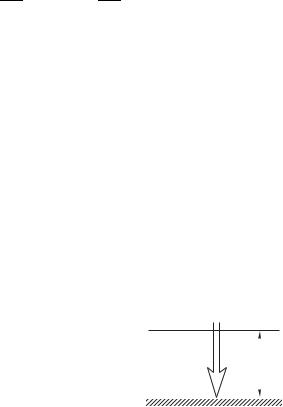
Первая из них более употребительна, по крайней мере в оптике. Дело в том, что при взаимодействии света с веществом, и в частности при его регистрации, б´ольшую роль играет именно электрический вектор. Взаимодействие происходит почти исключительно с электронами. Электрическое поле действует на элек-
10.4 ] |
Энергия и импульс электромагнитной волны |
343 |
трон с известной силой D , а магнитное — с силой Лоренца, которую можно оценить следующим образом:
D D- 7 D-,
так что для нерелятивистского электрона ( ) она дает лишь малую поправку. Поэтому принято плотность энергии, поляризацию света, сдвиг фазы и т. д. привязывать именно к электрическому полю.
Продолжим исследование энергетических характеристик волны. Вычислим вектор Пойнтинга
1 ! 1 !-2 !
!0 !0
Для поперечной волны последний член в правой части равен нулю, что позволяет упростить выражение:
|
|
<0- |
2 = |
|
|
||
!000 |
|
||
Поток энергии осциллирует во времени и пространстве, но всегда направлен вдоль вектора k. Средний по периоду или длине волны поток энергии в направлении k равен
= |
(10.21) |
|
|
Теперь не представит труда определить и среднюю плотность импульса поля в электромагнитной волне, исходя из соотноше-
ния (9.28): |
|
|
|
|
|
|
||
|
|
|
|
|
A |
(10.22) |
||
|
|
|
|
|
|
|
|
|
|
|
" |
72 |
7 |
||||
|
|
|||||||
Его можно трактовать следующим образом: «плотность массы» поля = 2 умножается на скорость ее «течения» . Это соотношение оказалось одним из основополагающих в разработ-
ке идеи световых квантов. |
|
|
|
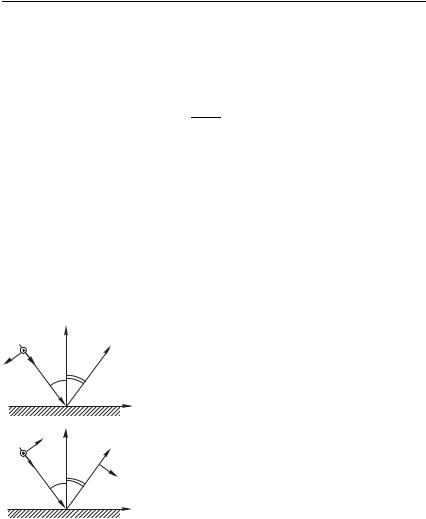
Представим себе, что плоская моно- |
k |
||
хроматическая электромагнитная волна |
|
|
|
|
|
||
падает нормально на абсолютно черную |
|
ct |
|
плоскую поверхность, где энергия поля |
|
||
|
|
||
полностью поглощается (рис. 10.2). За |
|
|
|
промежуток времени поверхности до- |
|
|
|
|
|
||
стигнет фронт (поверхность постоянной |
|
|
|
фазы), первоначально отстоявший |
от |
Рис. 10.2 |
|
плоскости на расстоянии . За |
это |
|
|
время поле, заключенное между указанным фронтом и плоско- |
|||
стью, полностью передаст последней свои импульс и энергию. |
|||
Таким образом, участок черной плоскости единичной площади |
|||
344 |
|
|
|
|
|
Электромагнитные волны |
|
[ Гл. 10 |
|||
воспримет за это время импульс |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
( |
|
|
7 |
|
|
Следовательно, волна, падающая нормально на черную поверх- |
|||||||||||
ность, оказывает на нее давление |
|
|
|
||||||||
|
|
|
|
|
|
|
2& = |
|
(10.23) |
||
|
|
|
|
|
|
|
( |
|
|
|
|
|
Эффект светового давления был подтвержден эксперимен- |
||||||||||
тально в 1899 г. выдающимся русским физиком П. Н. Лебеде- |
|||||||||||
вым (1866–1912). В случае черной облучаемой поверхности оно |
|||||||||||
равно средней плотности энергии в падающей волне, в случае |
|||||||||||
зеркально отражающей поверхности оно должно быть в два |
|||||||||||
раза больше, поскольку отраженная волна уносит тот же по |
|||||||||||
абсолютной величине импульс, но противоположного знака. Эту |
|||||||||||
ситуацию мы рассмотрим подробнее, не ограничиваясь случаем |
|||||||||||
нормального падения. |
|
|
|
|
|
||||||
|
Идеальное зеркало — это идеально проводящая поверхность. |
||||||||||
Любые зеркала, используемые в обиходе и в технике, действу- |
|||||||||||
ют именно по принципу отражения электромагнитной волны от |
|||||||||||
|
|
|
|
|
|
проводящей поверхности. Мы не будем |
|||||
|
E |
z |
|
à |
|
подробно разбирать всю относящуюся к |
|||||
|
|
|
|
|
делу |
электродинамику, |
ограничившись |
||||
|
|
|
|
|
|
||||||
|
k |
|
|
|
|
классической модельной задачей — отра- |
|||||
B |
|
|
|
|
|||||||
|
|
|
жением плоской монохроматической волны |
||||||||
|
|
|
|
|
x |
при косом |
падении |
на |
идеально прово- |
||
|
|
|
|
|
дящую плоскость в случае двух различ- |
||||||
|
|
|
|
|
|
||||||
|
|
z |
|
|
|
ных поляризаций (рис. 10.3 а, б). Угол |
|||||
|
E |
|
á |
|
между вектором k и нормалью к плоско- |
||||||
B |
|
|
|
|
|
сти принято называть углом падения. |
|||||
k |
|
|
|
|
Сам факт появления отраженной вол- |
||||||
|
|
|
E |
|
|||||||
|
|
|
|
||||||||
|
|
|
|
ны отнюдь не постулируется, но с необхо- |
|||||||
|
|
|
|
|
x |
димостью следует из граничных условий. |
|||||
|
|
|
|
|
Внутри |
идеального |
проводника должно |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
быть 0. Значит, на границе, т. е. при |
|||||
|
Рис. 10.3 |
|
|
0, должно быть |
0. Поскольку |
||||||
|
|
|
|
|
|
это заведомо не так в падающей волне |
|||||
(которой мы присвоим индекс |
), приходится ввести еще одну |
||||||||||
волну — отраженную (индекс ): |
|
|
|
||||||||
0 ! ; 0 !1 1 (10.24)
Если бы частота 1 была отлична от , мы не смогли бы выполнить граничное условие нулевого поля в любой момент времени. Поэтому частота отраженной волны, а значит, и волновое числодолжны совпадать с таковыми у падающей волны. Мы опустили в формулах (10.24) начальную фазу, поскольку у одной
10.5 ] |
Излучение электромагнитных волн |
345 |
волны она устраняется выбором начала отсчета времени, а у другой возможный фазовый сдвиг будет учтен знаком амплитуды.
Рассмотрим геометрию задачи, представленную на рис. 10.3 а. При такой поляризации вектор электрического поля параллелен проводящей плоскости, вектор магнитного поля лежит в плоскости падения. Условие 0 в начале координат0 в терминах формул (10.24) означает просто
0 0,
или, что то же, фазовый сдвиг в $ при равных амплитудах — обычно говорят: «потеря полуволны». Далее будем перемещаться вдоль границы, меняя координату . Условие 0 должно быть выполнено в любой точке границы, но зависимость от полей, при одинаковых волновых числах и 0 будет различной: ! ; !1 B, где B — угол отражения на рис 10.3 а. Единственная возможность надлежащим образом выполнить граничное условие на проводящей поверхности обеспечивается известным школьным правилом: угол падения равен углу отражения, B.
Рассмотрим случай другой поляризации, представленный на рис. 10.3 б. Теперь тангенциальные компоненты электрического
поля равны - - 0 ; - - 0 B. Условие сохранения частоты при отражении универсально; обеспечив нулевое
касательное поле в одной точке и требуя сохранения этого нуля в любой точке проводящей плоскости, получаем снова B Возвращаясь к выражениям для тангенциальных компонент поля, еще раз получаем 0 0, т. е. и в такой геометрии отражение происходит с потерей полуволны. Резюмируя, можно сказать, что мы построили количественную теорию идеального зеркала.
Важное замечание: граничное условие (9.12) — именно для тангенциальной компоненты E — выбрано нами не случайно. Анализируя полученные нами условия, читатель может самостоятельно убедиться, что они не могут обеспечить ни непрерывности , ни непрерывности Но на поверхности проводника полем волны индуцируются поверхностные токи и заряды, которые и балансируют соответствующие скачки — см. условия (9.14), (9.15) в расширенной форме. Условие (9.12) является более жестким — никакая реакция среды не может его подправить.
10.5. Излучение электромагнитных волн
Самый популярный излучатель в школьной физике — точечный источник света. Попробуем понять, может ли действительно излучатель электромагнитных волн обладать такими свойствами. При этом необходимо особо подчеркнуть, что дело не только
346 |
Электромагнитные волны |
[ Гл. 10 |
в малости генератора излучения. Одно из важнейших свойств точечного источника — отсутствие какого-либо выделенного направления и, следовательно, абсолютная изотропия излучения.
Таким образом, подобный источник может порождать только сферическую волну. Но сферической электромагнитной волны просто не может быть. Это нетрудно понять, вернувшись к мысленному эксперименту, представленному на рис. 9.1. В сферически симметричной конфигурации электрическое поле E может быть направлено только по радиусу, а магнитное поле должно быть тождественно равно нулю. Это и неудивительно, поскольку любые перемещения в сферически симметричной зарядовой системе, сохраняющие ее симметрию, оставляют поле E вне ее неизменным в силу теоремы Гаусса. Следовательно, вне такой системы 0 и 0, так что и 0 Но тогда тождественно равен нулю и вектор Пойнтинга, так что об электромагнитной волне вообще говорить не приходится.
Это не означает, что модель точечного источника в оптике является ошибочной. Просто во многих задачах можно рассматривать поле малого излучателя усредненным во времени. Будучи
вкаждый момент асимметричным, оно за характерное время регистрации может в среднем оказаться симметричным в достаточной степени, чтобы мы считали излучение изотропным, а излучатель — истинно точечным. При этом, правда, постановка вопроса о направлении электрического и магнитного поля излучения теряет смысл.
Что же касается стандартного утверждения типа «линза преобразует плоскую волну в сферическую, сходящуюся в фокусе», то оно верно лишь как некоторое приближение, в котором малым параметром служит телесный угол , охватывающий сходящийся пучок света. Истинная волна, сформированная линзой, мало отличается от сферической, пока и поскольку 1 Во всяком случае, из уравнений Максвелла следует, что ни сферической, ни цилиндрической электромагнитной волны в точном смысле не существует, а значит, не может быть слишком симметричным излучатель.
Оказывается, самым простым и фундаментальным типом излучателя является электрический диполь с переменным во времени дипольным моментом. Формальный уровень нашего курса не дает возможности изложить этот вопрос с должной степенью строгости, но мы можем сопроводить это утверждение достаточно убедительными аргументами.
Обратимся к уравнениям (10.10). Заметим, что первое из них
впринципе можно рассматривать как часть второго, если под 7 понимать любую компоненту вектора A. Вернемся к сферически симметричной модели и поищем соответствующее решение урав-

10.5 ] |
Излучение электромагнитных волн |
347 |
нений (10.10). Оператор Лапласа применительно к скалярной величине 7 при условии, что последняя зависит только от радиуса, но не от полярного или азимутального угла, может быть записан в простой форме, которую читатель может получить в виде упражнения, перейдя от декартовых координат к полярным:
|
27 22 22 22 |
|
1 2 2 2 2 |
|
22 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
2 2 2 |
#2 # # # # |
#2 |
||||||||||
Подставим его в первое уравнение (10.10), после чего умножим обе части уравнения на . Результат
22 |
2 2 1 2 #2 |
|
#2 |
# |
2 2 |
можно преобразовать к виду
2 |
1 |
2 |
, |
7 |
||||
# |
2 |
|
2 |
|
2 |
|||
|
|
|||||||
|
|
|
|
|
||||
Полученное уравнение формально одномерное, подобно (10.5), а следовательно, имеет решение
7 # |
|
(10.25) |
|
|
|
Решение (10.25) представляет, во-первых, пример истинно сферической волны (но она существует лишь для скалярной величины или потенциального вектора)
7 , 2 ## ,
а во-вторых, если рассматривать 7 еще и как компоненту вектора, моделирует так называемые запаздывающие потенциалы. Если, например, речь идет об электромагнитном поле, то потенциалы и , созданные соответственно токами и зарядами некоторой ограниченной в пространстве системы, устанавливаются на далеких от нее расстояниях с задержкой во времени .
Представим себе дипольную систему, которую мы на больших расстояниях можем описать просто дипольным моментом
, Для удобства описания излучения волн немецкий физик
Генрих Герц (1857–1894) ввел специальный вектор (его так и называют — вектор Герца)
, # 7 ,
#
который, как следует из (10.25), является решением волнового уравнения при 4 , т. е. представляет динамику типа электромагнитной волны. Если мы заставим диполь осциллировать во времени, 0 , то в достаточно удаленной от диполя области пространства эти осцилляции будут регистрироваться именно как бегущая электромагнитная волна.
348 |
Электромагнитные волны |
[ Гл. 10 |
Далее проведем мысленный эксперимент. Пусть наш диполь движется с постоянной скоростью. Тогда он, очевидно, излучать не будет; поле его будет просто стационарным полем в движущейся системе отсчета. Значит, поле излучения определяет не скорость, а, по крайней мере, следующая временн´ая производная, т. е. ускорение, пропорциональное 2 Точный расчет подтверждает такое заключение, а полная мощность излучения колеблющегося диполя дается выражением
|
1 |
2 |
|
4 |
|
|
&0 |
|
|
(10.26) |
|
) |
|
|
|
||
1200 |
73 |
|
|||
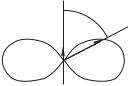
Это излучение обладает заметной анизотропией. Среднее за период значение вектора Пойнтинга оказывается пропорциональным sin2 , где — полярный угол,
который отсчитывается от направления дипольного момента (рис. 10.4).
p0 |
Из всего |
вышеизложенного следует, |
|
|
S( ) |
в частности, |
принципиальная трудность |
|
|||
|
|
резерфордовской планетарной модели ато- |
|
|
|
||
|
|
ма. Если бы электрон просто вращался по |
|
орбите вокруг ядра, атом в принципе существовал бы конечное время — пока вся начальная кинетическая энергия не ушла бы с излучением. Тогда
произошло бы падение электрона на ядро. Существенно, что в этом случае свойства отдельных атомов не были бы идентичны, а зависели бы от возраста. Это соображение послужило главным толчком к созданию атомной модели Бора, а далее — и всей квантовой механики.
Формула (10.26), а равно и рис. 10.4, подразумевают, что
размер диполя меньше длины волны : . Такой диполь называют элементарным диполем или диполем Герца. Излуче-
ние может быть надежно идентифицировано в так называемой волновой зоне — при . В технических целях используются обычно другие излучатели — антенны, у которых характерный размер, с тем или иным коэффициентом порядка единицы, соответствует как раз длине волны: 2$ Если излучение элементарного диполя может быть вызвано различными причинами, включая ускорение частиц, то в случае антенны это всегда результат подачи на диполь мощного внешнего сигнала.
Электродипольное излучение — наиболее типичный механизм генерации электромагнитных волн и в природе, и в технике, но в принципе существуют и другие, связанные с изменением во времени магнитодипольного момента, электрического и магнитного квадрупольных моментов и т. д.
10.6 ] |
Задачи |
349 |
Задачи
1. Плоская монохроматическая электромагнитная волна частоты падает нормально на плоскую гладкую поверхность проводника (см. рис. 10.2). Проводимость материала , магнитная проницаемость ! 1 Оценить коэффициент
отражения по мощности и амплитуде.
Решение. Отличие коэффициента отражения от единицы обусловлено джоулевой диссипацией в скин-слое, т. е. на глубине вплоть до Æэф, которая дается формулой (8.28):
Æэф 2 !0
Удобно вычислять связанные с этим потери, относя их к единице площади поверхности зеркала, а затем получить коэффициент отражения, нормируя эту диссипацию на поток энергии. Итак,
2> 32 |
|
2 2 |
|
||
|
|
|
Æэф * |
|
|
( |
|
!0 |
|||
Модуль вектора Пойнтинга, равный потоку энергии на поверхность зеркала, можно представить в виде
2
*2 *
!0 |
7!0 |
Отнеся интенсивность потерь к потоку энергии, получим коэффициент поглощения по энергии; вычитая последний из единицы, получим коэффициент отражения по мощности . (К сожалению, это совершенно стандартное обозначение пересекается с принятым в электротехнике символом омического сопротивления). Таким образом,
1 |
2 |
|
7!0 |
1 7 |
2!0 |
|
|
|
|
||||
!0 |
|
|
||||
|
|
|
|
|||
Поскольку отраженная волна представляет собой электромагнитную волну той же частоты, что и падающая, и с тем же соотношением между E и H, амплитудный коэффициент отражения равен просто квадратному корню из
коэффициента отражения по мощности: # Надо заметить, что использованные нами соображения корректны лишь в случае радиоволн достаточно низкой частоты. В оптическом и даже инфракрасном диапазоне частот механизмы отражения и потерь будут несколько иными. Мы еще коснемся этого вопроса в заключительной главе.
Точность полученных нами результатов не слишком велика — именно потому, что не слишком точно оцененную величину приходится вычитать из единицы. Гораздо более надежна оценка коэффициента поглощения по мощности
1 7 2!0 ,
которая позволяет правильно оценить порядок величины потерь при отражении. Качественным ответом задачи будет либо малость этого коэффициента
всравнении с единицей, либо соизмеримость.
2.Электрон совершает циклотронное вращение в однородном магнитном поле B. Получить зависимость его энергии от времени и оценить, сколько оборотов он сделает до остановки.

350 Электромагнитные волны [ Гл. 10
Решение. Мы неоднократно подчеркивали гироскопический характер силы Лоренца, в силу которого она не совершает работы над заряженной частицей. Но при движении частицы по круговой орбите (а это движение с ускорением) происходит, в соответствии с (10.26), излучение электромагнитных волн, оното и тормозит частицу. Мы сделаем лишь одно упрощающее предположение: пусть энергия, потерянная на излучение за один оборот, будет много меньше кинетической энергии электрона. Необходимое для этого условие последует в конце решения.
Дипольный момент единственной частицы равен (см. (1.23)): < . Удобно поместить начало координат в центре циклотронной орбиты, тогда &0 < , где — скорость электрона на орбите, а < — циклотронная частота. Поскольку диполь в данном случае вращается, а не
осциллирует, интенсивность потерь (10.26) нужно удвоить (складывая |
4 &2 |
||||||||
|
|||||||||
и 4 &2 ): |
2 4 |
|
2 2 2 |
|
|
2 2 |
|
|
|
> |
1 &0 |
< |
|
> < |
|
, |
|
||
|
|
|
|
|
|
|
|
||
600 73 |
60073 3 0073 |
|
|||||||
|
|
|
|||||||
где > — кинетическая энергия. Составляя уравнение > > , находим, что кинетическая энергия электрона должна убывать по экспоненциальному
закону |
|
|
|
|
|
|
|
|
|
|
1 <2 2 |
|
|||
> |
|
|
|
|
|
|
|
|
3 |
|
3 |
||||
|
|
007 |
|
||||
Как обычно при экспоненциальном затухании, характерное время остановки не зависит от начальной энергии — по смыслу это масштаб времени, по истечении которого энергия становится существенно меньше начальной. Это время можно выразить через характерное число оборотов:
. 3 |
20073 |
|
|
B |
|
|||
< |
2 2 |
|||||||
|
||||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
Отсюда и получаем ответ |
|
|
20073 |
|
|
|
||
B 3 |
|
|
|
|||||
|
|
|
|
|||||
|
|
<3 |
|
|
||||
Наше предположение о малости потерь за период эквивалентно сильному неравенству B 1, что приводит к следующему условию на поле:
3 20073< 3 1012 Тл
—оно с запасом выполнено при всех доступных значениях поля. Соответственно, с большим запасом выполнено условие B 1, так что при рассмотрении не слишком большого числа оборотов частицы в магнитном поле мы вполне можем пользоваться приближением стационарной орбиты (как это до сих пор и делалось).
3.Плоская монохроматическая электромагнитная волна падает нормально на отражающую поверхность, частично поглощается, а частично отражается. В пространстве перед зеркалом образуется суперпозиция падающей и отражен-
ной волн, причем т. н. коэффициент стоячей волны — отношение амплитуды в пучности к таковой в узле — равен 10 Определить коэффициент отражения по мощности.
Ответ: |
|
|
1 |
2 |
|
|
1 |
0,67 |
|
|
|
|
||
