студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

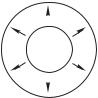
Г л а в а 9

УРАВНЕНИЯ МАКСВЕЛЛА

9.1. Ток смещения. Обобщение теоремы о циркуляции

Данную тему мы начнем с мысленного эксперимента. Представим себе заряженный сферический конденсатор (рис. 9.1), у которого пространство между обкладками заполнено однородным диэлектриком. Пусть заряды обкладок равны C. Предположим, что в некоторый момент времени диэлектрик практически мгновенно и всюду однородно переводится в проводящее состояние. В случае мысленного эксперимента неважно, как именно это сделано — скажем, импульсом ионизирующего излучения.

ре, в случае достаточно медленного процесса разрядки. Действительно, если при протекании тока нигде в диэлектрике не происходит накопления заряда, ток через любую сферическую поверхность, концентрическую с обкладками, должен быть одинаков, а значит, плотность тока обратно пропорциональна площади сферы.

При попытке применить теорему о циркуляции в форме (4.10) мы столкнулись бы с очевидным абсурдом. Единственно разрешенным направлением для H в случае столь высокой симметрии было бы радиальное направление . Но эта возможность исключена теоремой Гаусса для магнитного поля (4.1), поскольку такая конфигурация отвечала бы магнитному заряду в центре симметрии. Таким образом, единственно разумный ответ в данной задаче — нулевое магнитное поле. А в то же время, приложив формулу (4.10) к любой токовой трубке, мы получили бы

0. Значит, мы должны так модифицировать теорему (4.10), чтобы в данной задаче получить строго нуль в правой части.

11 Основы физики. Т. I

322 Уравнения Максвелла [ Гл. 9

зависит. Таким образом, модификация теоремы (4.10) должна «замкнуть» ток через конденсатор.

Удобнее все же вносить поправки не в формулу (4.10) как таковую, а в соответствующее ей локальное уравнение (4.12):

rot

Вернемся к ситуации, изображенной на рис. 9.1. Поправка, обращающая для этого случая в нуль правую часть (4.12), долж-

Интеграл по поверхности 9 рис. 9.2 даст просто полный ток :.

Величина, представленная формулой (9.1), называется плотностью тока смещения, а поток от нее — соответственно, током смещения. К тому же результату можно прийти и другим путем,

исходя из закона сохранения заряда (3.7):

% 0

Если мы возьмем дивергенцию от уравнения (4.12), то в левой части получим нуль: div (rot H) 0 Значит, нуль должен получиться и в правой части нового уравнения

% , что тождественно удовлетворяется как раз добавкой (9.1). Все

приведенные рассуждения являются хорошими аргументами в пользу (9.1), но отнюдь не бесспорными доказательствами, и окончательное слово остается, как обычно в физике, за

вместе с законом Ома и т. п. выделяют в особую группу и называют материальными уравнениями, тогда как уравнениями

Максвелла считаются именно (9.2)–(9.5).

Как мы уже могли убедиться, для решения многих, в особенности простых, задач может быть весьма полезна интегральная форма уравнений Максвелла — совершенный эквивалент фор-

мул (9.2)–(9.5):

Любое уравнение можно брать в любой форме, локальной либо интегральной, руководствуясь исключительно соображениями удобства. Система уравнений Максвелла решается при следующих граничных условиях на поверхности:

Напомним, что квадратные скобки здесь означают скачок соответствующей величины на поверхности. В правой части двух последних уравнений стоит´ нуль или, соответственно, поверхностная плотность заряда и тока в зависимости от того, рассматриваем ли мы истинную границу или представляем в качестве таковой слой с толщиной много меньшей характерного пространственного масштаба задачи.

Было бы заблуждением считать, что граничные условия (9.12)–(9.15) нами уже были выведены. Мы действительно получали каждое из них в главах 2 и 5, но при существенных упрощающих предположениях. Например, условие (9.12) получено для случая потенциального поля, которое тождественно обратило бы в нуль левую часть (9.3) или (9.9). В определенном смысле граничные условия следуют из самих уравнений (9.2)–(9.5) и точно так же должны рассматриваться как обобщение экспериментальных данных.

Электрическое поле при учете эффекта электромагнитной индукции теряет свойство потенциальности. Но оказывается,

добавление в систему уравнений введенного в гл. 4 вектор-потен- циала позволяет в принципе представить два вектора E и H как функции двух потенциалов. Не останавливаясь на этом вопросе подробно, ограничимся случаем поля в вакууме:

Взяв ротор от выражения для E, получим уравнение (9.3), а дивергенция H оказывается нулевой, как и следует из (9.5) для поля в вакууме. Можно видеть, что, как мы уже заметили в гл. 6, ЭДС, т. е. непотенциальность электрического поля, обязательно связана с нестационарностью.

Из уравнений (9.16) вытекает весьма полезное свойство потенциалов, которое принято называть калибровочной инвариантностью. Физически наблюдаемыми (измеряемыми) величинами являются поля E и H, между тем, даже в электростатике потенциал определен лишь с точностью до аддитивной постоянной. Обратившись к первому уравнению (9.16), нетрудно заметить, что магнитное поле не изменится, если к величине A мы добавим градиент любой скалярной функции B, поскольку ротор любого градиента равен нулю (отсюда ранее употреблявшийся термин — «градиентная инвариантность»). Но для того чтобы из второго уравнения (9.16) получилось то же самое поле E, следует к скалярному потенциалу добавить величину 10.B .. Таким образом, уравнения Максвелла в общем случае оказываются инвариантными относительно следующей замены:

B

Очевидно, добавление к произвольной константы, не зависящей от координат, есть частный случай преобразований (9.17).

9.3.Теорема Пойнтинга

Впредшествующих главах мы расширили известное из механики понятие энергии, введя корректным образом энергию электрического, а затем и магнитного поля. Теперь, базируясь на уравнениях Максвелла, мы можем проследить, как эволюционирует энергия поля в динамической задаче. Это, в свою очередь, позволяет распространить закон сохранения энергии на такие среды, в которых существенно взаимодействие поля с веществом.

Итак, мы исходим из выражений (2.29) и (7.11). Таким образом, плотность энергии электромагнитного поля (если ее можно

джоулевой диссипацией и, во-вторых, «вытеканием» энергии через поверхность, ограничивающую данный объем. Вектор потока электромагнитной энергии

называется вектором Пойнтинга по имени английского фи-

зика Дж.Г. Пойтинга (1852–1914), а закон эволюции энергии в замкнутом объеме (9.22) — теоремой Пойнтинга. Ее можно

представить и в локальной форме. Для этого последний интеграл в правой части нужно оставить в виде объемного, а левую часть — также в виде объемного интеграла от плотности энергии. Поскольку объем интегрирования может быть совершенно произвольным, должны быть равны подынтегральные выраже-

В таком виде теорема Пойнтинга напоминает закон сохранения заряда (3.7), только в данном случае имеет место еще и сток энергии в тепло через джоулеву диссипацию. При отсутствии таковой мы получили бы точный закон сохранения электромагнитной энергии.

А теперь перейдем от линейной среды к общему случаю произвольной зависимости , . Пока и поскольку мы могли выделить энергию электромагнитного поля аддитивным образом, эта связь предполагалась линейной. Следовательно, в общем случае мы не сможем отделить друг от друга энергию поля, энергию вещества и энергию взаимодействия поля с веществом. Но поскольку расширение понятий и зависимостей представляется гораздо более естественным, нежели их полная ревизия, имеет смысл распространить и на этот случай действие теоремы Пойнтинга, доопределив все остальные добавки к энергии и потоку энергии как взаимодействие поля с веществом. При таком определении мы как бы узаконим проведенную выше операцию:

Таким образом, работа по изменению электрического и/или магнитного поля — каким бы образом она ни совершалась — может быть представлена в виде

Рассмотрим пример. Предположим, что мы поместили ферромагнитный образец в периодическое внешнее магнитное поле. По прошествии каждого периода он неукоснительно возвращается в исходное состояние. Этот процесс требует энергетических

затрат, которые пропорциональны (с точностью до размагничивающего фактора) площади, охватываемой кривой гистерезиса:

C1 2 * ! G

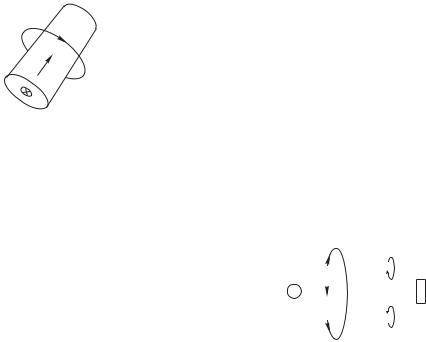
Далее рассмотрим некоторые простые примеры вычисления вектора Пойнтинга. Представим себе цилиндрический проводник, по которому течет ток с равномерно распределенной по сечению плотностью j (рис. 9.3). Электрическое поле вне провода вблизи его поверхности должно быть, согласно условию (9.12), таким же, как и внутри, т. е. , магнитное поле G : 2$ " 2, соответственно, вектор Пойнтинга

нормален к поверхности проводника, направлен внутрь него и равен

Другой пример представлен на рис. 9.4. Длинная двухпроводная линия соединяет источник постоянной ЭДС и нагрузку — сопротивление . Полагая сопротивление подводящих проводов пренебрежимо малым, определим направление вектора Пойнтинга. Мы при этом ограничимся малой окрестностью проводов. Направление магнитного поля задается правилом буравчика (см.

ния в данной геометрии, нетрудно убедиться в том, что в любой точке вектор Пойнтинга будет «показывать» на нагрузку, что вполне естественно: в стационарной задаче поток энергии должен быть направлен туда, где происходит диссипация, поскольку ) 0.

Отметим важное обстоятельство. Из теоремы Гаусса следует, что оба провода в данной системе должны быть заряжены, что не

всегда правильно понимается при решении задач на протекание тока в твердом проводнике. В отличие от электростатики, здесь не поле задается зарядом, а заряд — полем, которое следует из разности потенциалов :. Но все закономерности, изученные нами ранее, продолжают работать, и забывать об этом не следует.

9.4. Импульс электромагнитного поля

Мы достаточно много внимания уделили проблеме энергии электромагнитного поля, но поле обладает, вообще говоря, также и импульсом, распределенным, подобно энергии, в пространстве с некоторой плотностью Ввести его корректным образом было бы на уровне нашего курса непросто, но мы можем сделать это на основании достаточно очевидных аналогий.

Как мы уже выяснили, вектор Пойнтинга — это вектор потока энергии, т. е. модуль его есть энергия, переносимая электромагнитным полем в единицу времени через площадку единичной площади, ориентированную перпендикулярно вектору потока. (А если площадка ориентирована как-то иначе, для вычисления той же величины нужно взять проекцию вектора Пойнтинга на нормаль к площадке.)

Это не единственная потоковая величина, с которой мы имели дело. Например, вектор плотности тока j можно с равным правом именовать вектором потока заряда, поскольку он представляет собой как раз заряд, протекающий в единицу времени через единицу площади поперечного сечения проводника. Как мы уже убедились (см. гл. 3), в случае единственного сорта носителей заряда его можно достаточно просто выразить через концентрацию заряженных частиц и их локальную скорость:

D

Теперь представим себе, что вместо заряда, мы подставили в эту формулу массу частиц. Тогда, очевидно, мы получим выражение для потока массы

Вслучае течения многокомпонентного газа (жидкости, плазмы) это выражение следовало бы просуммировать по сортам частиц, но для наших рассуждений в этом нет надобности. Нетрудно заметить, что поток массы представляет собой не что иное, как пространственную плотность импульса среды:

Соотношение (9.26) остается в силе и в релятивистском случае, если под массой понимать не массу покоя, а так называемую ре-

лятивистскую массу , которая как самостоятельная величина в настоящее время употребляется редко — предпочитают просто выражать ее через полную энергию частицы (к сожалению, стандартное обозначение энергии в релятивистской механике пересекается с не менее стандартным обозначением ЭДС):

т. е. плотность импульса с точностью до коэффициента 1 2 есть поток энергии частиц. И вот этот результат, абсолютно строгий в случае течения вещества, мы и перенесем на электромагнитное

Из формулы (9.28) можно извлечь несколько поучительных следствий. Во-первых, как нетрудно видеть, чисто электрическое или чисто магнитное поле импульсом не обладают. Во-вторых, если , плотность импульса также равна нулю. В-третьих, представим себе одну из названных ситуаций и предположим, что мы перешли в некоторую движущуюся систему отсчета. Поле, как мы теперь понимаем, имеет массу. Следовательно, в новой системе отсчета у поля окажется ненулевой плотность импульса, а это значит, в согласии с (9.28), в новой системе отсчета обязательно должны быть представлены оба поля , , и притом не параллельные друг другу. Справедливо и обратное: можно показать, что мы всегда можем перейти в такую систему отсчета, в которой импульс электромагнитного поля равен нулю,

т. е. существует или только , или

через сопротивление и возвращается по соосному с соленоидом прямому проводу радиуса 1. Найдем вектор Пойнтинга внутри катушки вдали от ее торцов, считая пренебрежимо малыми сопротивления как соленоида, так и соединительных проводов. При таком предположении разность потенциалов между обмоткой соленоида и центральным проводом равна : Электрическое