студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

деляется и эффективное значение тока — как постоянный ток, эквивалентный данному переменному по тепловому эффекту;

соответственно, :эф :0 2 .

Предположим, что мы имеем дело с цепочкой, изображенной на рис. 8.2, но теперь в контур последовательно включен источник синусоидальной ЭДС, так что, в отличие от (8.6), (8.7), динамика тока в цепи определяется уравнением:

Как уже говорилось, решение линейного уравнения с правой частью может быть представлено как сумма любого частного решения, удовлетворяющего этому уравнению, и общего решения однородного уравнения (т. е. без правой части); последнее в случае уравнений второго порядка зависит от двух произвольных констант, согласующих его с начальным моментом времени. Действительно, пусть :1 и :2 — два решения (8.19), тогда разность :1 :2 должна быть, в силу линейности, решением уравнения (8.7).

Общее решение однородного уравнения можно взять в форме (8.11); оно с течением времени будет затухать. Характерное время затухания > 1 Æ. Частное решение будем искать в виде незатухающих колебаний с частотой приложенного напряжения —

Аналогичная зависимость от времени должна получиться для падения напряжения на любом элементе, заряда конденсатора и прочих динамических величин. Ради удобства последующих операций мы полагаем величину : в (8.20) комплексной — помимо собственно амплитуды :0 в нее входит и сдвиг фаз по отношению к внешней ЭВС. Подставляя (8.20) в (8.19), убеждаемся, что оно и в самом деле является решением. Комплексную амплитуду тока можно получить из уравнения

Нетрудно усмотреть прямую связь с формулами (8.17) — получился просто закон Ома в частном случае синусоидального напряжения и тока. Но теперь мы можем грамотно ответить на вопрос о процессе установления тока при включении внешней ЭДС, тем более важный, что фаза в момент включения не определена. Итак, включение переменного тока сопровождается «звоном» собственных колебаний контура, затухающим с характерным временем 1 Æ. Именно эти колебания обеспечивают согласование цепи с фазой источника. Если же мы, как обычно в электротехнике, интересуемся установившимися колебаниями

Отсюда можно понять, почему добротности присвоен столь «значащий» термин. Еще один вид резонанса — его называют резонансом токов — представлен на рис. 8.5 а, б. Для простоты будем считать сопротивление ка-

отставая по фазе на $ 2, вычисляются по уже известному нам

рецепту. И если : : — это получается при 1 +% , — то при отличном от нуля напряжении ток в неразветвленном участке цепи равен нулю. В действительности при учете активного сопротивления получается просто более или менее острый минимум тока, при этом импеданс цепи опять соответствует чисто активному сопротивлению.

Как пример отклика электрической цепи на несинусоидальную переменную ЭДС рассмотрим цепочки, изображенные на рис. 8.6. На входные клеммы подается некоторый сигнал с характерным временем эволюции > Можно для оценок пользоваться также характерной частотой в спектре сигнала > 1

Рис. 8.6

Отклик — напряжение — снимается с выходных клемм, как показано на рисунках; предполагается, что сопротивление измерительного прибора столь велико, что он не вносит заметного вклада в уравнение цепи. Тогда динамика цепочек рис. 8.6 а, б описывается уравнением

Мы рассмотрели все четыре случая, базируясь на оценках, но те же результаты можно получить и более строго на основе

фурье-разложения сигнала. Цепочки а, в на рис. 8.6 называют

интегрирующими, а б, г — дифференцирующими. (Разумеется, при этом важна не только схема включения, но и соотношения характерных времен, заданные выше.) Их часто используют в качестве элементов различных измерительных схем. Конечно, точность выполняемых ими операций не слишком высока — как

иу всех вообще аналоговых систем — зато они очень просты.

8.4.Скин-эффект

Внастоящем параграфе мы рассмотрим особый случай квазистационарных процессов — токи высокой частоты, для которых остаются справедливыми условия (8.1), (8.2), но теряется понятие электрической цепи как совокупности элементов с сосредоточенными параметрами. Тем самым будут получены дополнительные к (8.1), (8.2) условия того, что систему проводников можно

будет рассматривать как электрическую цепь.

Skin — по-английски «кожа», скин-эффект — протекание токов достаточно высокой частоты в тонком приповерхностном слое хорошего проводника. При этом в глубине проводящей среды ток может быть сколь угодно малым. Как мы вскоре убедимся, благоприятным условием для проявления скин-эффекта оказывается как можно более высокая проводимость вещества. Это может быть металл, а может и плазма, которая при термоядерных тем-

пературах 107–108 К по проводимости превосходит металлы примерно на порядок. Однако при достаточно высоких частотах скин-эффект характерен даже для человеческого тела — при контакте с источником происходит прогрев тонкого слоя кожи, но исключается поражение электрическим током. Сколь высока должна быть частота и сколь хороша проводимость, станет ясно из оценок, которые вскоре будут сделаны, а пока мы примем этот факт как экспериментальный.

Трактовать это явление можно по-разному, но в общем, классический скин-эффект вполне объясняется классической электродинамикой, и мы этим ограничимся, но не пойдем традиционным формальным путем, а построим наше изложение на фундаментальном принципе Ленца и его количественном выражении

— законе Фарадея (6.7):

Ради упрощения последующего рассмотрения предположим, что у проводящей среды 1 1, что всегда верно для плазмы и с хорошей точностью — для большинства хорошо проводящих металлов.

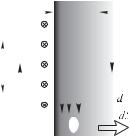
в гл. 7, — замедление падения монеты (строго говоря, любого проводящего тела), если в процессе падения она пересекает силовые линии магнитного поля, например, если мы ее роняем между полюсами мощного электромагнита. Это происходит, как мы уже выяснили, вследствие возбуждения ЭДС индукции и, как следствие, генерации индукционных токов.

Если бы внешнее поле совсем не проникало в проводящую среду, монета вообще бы повисла в воздухе — это случай так называемого магнитного удержания или вмороженности поля. Но она падает, хотя и медленно, значит, поле как-то все же в проводник просачивается. Чтобы понять, как это происходит, рассмотрим модельную плоскую задачу. Геометрия ее представлена на рис. 8.7. Пусть в начальный момент времени вне проводника существует однородное магнитное поле B, а в толще проводника поле равно нулю; скачок поля на границе поддерживается поверхностным током. Именно так должно случиться, согласно

принципу Ленца, при быстром включении

Чтобы рассмотреть эффект проникновения магнитного поля в среду (или, что то же, расширения токового слоя вглубь), дополним наши оценки законом Ома в локальной форме: . Заодно перейдем от общего закона (6.7) к конкретной оценке для контура А на рис. 8.7:

где E — коэффициент диффузии. (В нашем курсе процессы переноса, включая диффузию, будут подробно рассмотрены в заключительном — пятом разделе.)

Таким образом, поле (и ток) просачивается в проводящую среду по диффузионному закону. Так и говорят: диффузия магнитного поля. Этот результат получен нами в модельной задаче как следствие простых оценок, но он является совершенно общим, и выражение для коэффициента диффузии поля оказывается верным вплоть до коэффициента E 1 10

И вот теперь на базе этого результата мы немедленно и практически без вычислений сможем понять природу скин-эффекта. Пусть на границе проводника создано быстропеременное поле (как следует из теоремы о циркуляции, по ней при этом протекает быстропеременный ток). Оценим глубину, на которую продиффундирует поле за период,

!0

Если этот масштаб много меньше , где — характерный размер проводника, то поле и ток окажутся локализованы в более или менее тонком слое у поверхности. Отсюда можно получить и обещанные условия на частоту и проводимость. Существенным оказывается произведение этих двух величин. Если

то мы будем иметь дело не с однородным распределением тока по сечению проводника, которое до сих пор всегда молчаливо предполагали, но со скин-эффектом.

Точные решения системы уравнений электродинамики для плоского проводника, а равно и цилиндрического, если толщина скин-слоя много меньше его радиуса, дают

что, безусловно, демонстрирует очень хорошее соответствие с нашей простой оценкой.

В случае ярко выраженного скин-эффекта существенным образом меняются как сопротивление, так и самоиндукция проводников. Как следствие, цепь стремится превратиться в систему с распределенными параметрами. Если в формуле (8.29) в качестве фигурирует поперечный размер проводников, то это условие, не посягая на квазистационарность задачи — неравенства (8.1), (8.2) остаются в силе, в принципе ставит под вопрос само приближение электрической цепи. Таким образом,

при условии (8.29), возможно, придется перейти от сравнительно простой электротехники к полноценной электродинамической задаче.

Задачи

1. Последовательно соединенные дроссель и омическое сопротивление присоединены к источнику постоянного напряжения с ЭДС (рис. 8.8 а). Индуктивность дросселя, когда в него вставлен железный сердечник /, равна1, а без сердечника — 2. Вначале сердечник был вставлен, и ток в цепи установился. В момент времени 0 сердечник очень быстро вынимают (за время, много меньшее времени релаксации). Определить ток в цепи + при

E 0

Рис. 8.8

Решение. При быстром удалении сердечника изменяется индуктивность дросселя и ток через него, но магнитный поток измениться мгновенно не

может:

1 2+0,

где +0 — ток через дроссель в момент 0 В последующие моменты времени цепь подчиняется уравнению:

++ 2

Решение этого линейного уравнения с правой частью имеет вид

контура, если выводы второй катушки замкнуты накоротко? Считать, что активное сопротивление второй катушки пренебрежимо мало. При каком условии резонанс невозможен?