студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

7.5 ] Задачи 301

ветствуют параллельной и антипараллельной ориентациям диполей. При этом первый член в числителе (4.24) обращается в нуль, так что для энергии и силы взаимодействия получаются следующие выражения:

> 4 3 Æ 4 4

Уравнение баланса сил во вращающейся системе отсчета:

где , — гравитационная постоянная. Мы пренебрегли ради простоты ответа различием между массой планеты и приведенной массой, полагая, что наша поправка будет относительно больше, чем 0 Далее, представляя частоту

Искомая величина разброса периода обращения 2Æ, так что окончательный ответ выглядит следующим образом:

3.Один из способов получения сверхсильных магнитных полей — взрывное сжатие металлического лайнера, подобного изображенному на рис. 7.2 а,

внутри которого предварительно создается магнитное поле с индукцией 0. Определить индукцию поля в цилиндре в момент максимального сжатия, если

0 5 Тл, начальный внутренний радиус лайнера 0 5 см, радиус в момент максимального сжатия 0,5 см. Оболочку считать идеально проводящей.

Оценить давление, необходимое для такого сжатия. Ответ: 500 Тл, 106 атм.

4.Длинный цилиндрический стержень с магнитной проницаемостью !

иплощадью сечения ( расположен вдоль оси соленоида так, что один его конец находится внутри, а другой — вне соленоида. Найти силу , с которой

стержень втягивается в соленоид с собственным полем .

Г л а в а 8

КВАЗИСТАЦИОНАРНОЕ

ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

8.1. Условие квазистационарности электрической цепи. Релаксационные процессы

Основной предмет изучения в данной главе курса — электрические цепи переменного тока и, как частный случай — колебательный контур. В гл. 6 мы уже фактически рассматривали объекты такого рода в контексте закона электромагнитной индукции. При этом мы по умолчанию воспользовались некоторыми приближениями, которые обеспечили плавный переход от известных нам цепей постоянного тока.

Например, мы всюду вычисляли магнитное поле или векторпотенциал таким образом, как если бы они порождались постоянным током в проводнике. В последующих главах мы сможем строго определить границы применимости такого рассмотрения, однако представление о них желательно иметь уже сейчас. Физика, как и любая естественная наука, постоянно оперирует с моделями реальности (и лишь на этом уровне может называться «точной»). И мы можем правильно оценивать наши результаты лишь постольку, поскольку нам известна область применимости модели.

Как уже было замечено, нам еще предстоит дополнить теорему о циркуляции с учетом как раз временн´ой зависимости полей. Именно здесь возникает ограничение, которое принято называть условием квазистационарности, т. е. возможности распространять некоторые законы, установленнные для стационарных цепей, на нестационарные цепи. («Квази-» означает «как бы...».)

Это условие можно получить, основываясь на том общеизвестном факте, что электромагнитный сигнал распространяется в вакууме со скоростью света 3 108 м/с. В прозрачной среде (стекло) или специальной транспортирующей системе (волновод) эта скорость может быть меньше скорости света, но остается величиной того же порядка. Соответственно, если пространственный масштаб нашей системы (цепи) есть величина порядка , то характерное время установления полей или токов в цепи (инерционное время) можно оценить как

8.1 ] Условие квазистационарности электрической цепи 303

Естественно предложить следующее неравенство в качестве

где > — характерное время задачи. В частности, если речь идет о гармонических колебаниях либо переменном токе частоты , условие (8.1) эквивалентно следующему:

При обратном соотношении мы заведомо должны рассматривать нашу цепь как систему с распределенными параметрами, т. е. просто решать общую задачу электродинамики. Вообще говоря, при рассмотрении электрических цепей обычно по умолчанию предполагается выполненным условие тонкого провода , где— характерный поперечный размер проводника. Тем самым обеспечивается независимость результата от распределения тока по сечению провода, а значит, и от самовоздействия через собственное магнитное поле. Но в одном из типичных элементов цепи — конденсаторе — это условие никогда не выполняется, поэтому приближение системы с сосредоточенными параметрами раньше всего отказывает именно в емкостном элементе.

Обсуждая условия квазистационарности, мы все время адресуемся к теореме о циркуляции. Полезно отметить также, какие законы, напротив, никак не меняются при переходе от стационарных полей к переменным. Во-первых, остается в силе теорема Гаусса как для электрического поля, так и для магнитного. (Это, правда, справедливо без оговорок лишь для точного — микроскопического — поля. Но мы уже говорили о неуниверсальности процедуры усреднения и ее результата.) Во-вторых, и это даже более интересно, остается в неприкосновенности закон электромагнитной индукции (6.10). Этот факт можно считать экспериментальным. Но тогда из теоремы Стокса следует, что сохраняет силу и интегральная форма закона Фарадея (6.7). Последнее обстоятельство выглядит отнюдь не тривиальным. Действительно, контур, быть может, не удовлетворяет условиям квазистационарности (8.1), (8.2), так что поле протекающих в нем токов нельзя рассматривать как безынерционное, тем не менее, интегральный закон (6.7) сохраняется в качестве одного из фундаментальных.

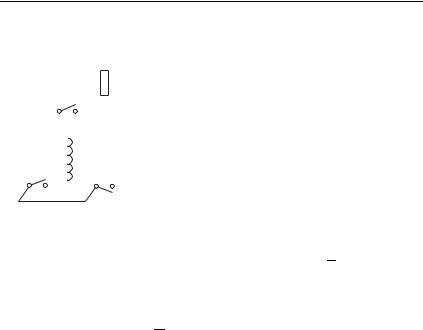
Пусть условие (8.1) выполнено. В качестве простейших примеров рассмотрим так называемые релаксационные или переходные процессы в цепях, представленных на рис. 8.1 а, б.

Пусть конденсатор % на рис. 8.1 а заряжен при разомкнутом ключе и отсоединен от источника. В качестве начального условия можно взять, например, заряд на обкладках C0. Замы-

304 Квазистационарное электромагнитное поле [ Гл. 8

каем ключ и определяем момент замыкания как 0. Далее

Тот же результат можно получить и другим способом, скажем, составить закон Кирхгофа

;1 : : 0,

а затем продифференцировать его по времени, и мы снова придем

к тому же соотношению. Величина > % называется постоянной времени или временем релаксации %-цепочки. Именно

эту величину следует подставлять в неравенство (8.1), оценивая пределы применимости модели.

Обратимся к +-цепочке, представленной на рис. 8.1 б. Пусть вначале через катушку индуктивности + протекает некоторый ток :0, а затем в момент времени 0 одновременно размыкается ключ и замыкается ключ ; таким образом, в начальный момент задается величина тока :0 в катушке. Уравнение для тока в цепи можно представить, например, в виде закона

так что время релаксации >+ + Сколь бы ни было велико сопротивление, в течение этого времени ток остается по порядку величины близким к начальному. Значит, чем выше сопротивление, тем больше и пик напряжения, приходящийся на время релаксации. Этим и объясняется «искр´ение» при быст-

ром обрыве тока в цепи конечной индуктивности: напряжение

вмаксимуме оказывается выше пробойного для воздушного промежутка. Обратный эффект наблюдается при включении тока

вцепи: индуктивность затягивает установление стационарного состояния. Пусть в момент 0 была замкнута цепь, состоящая

из последовательно включенных источника постоянной ЭДС 0, индуктивного элемента + и сопротивления . Ток как функция времени подчиняется уравнению

+

+ : 0

Его общее решение состоит, как известно, из суммы любого частного решения и общего решения однородного уравнения

+ + : 0, содержащего одну произвольную константу; последняя позволяет

«привязать» решение к заданным начальным условиям. В нашем случае в качестве частного решения удобно выбрать просто константу : 0 , а общее решение однородного уравнения имеет вид (8.4) с произвольной постоянной :0. Полагая ток в начальный момент времени равным нулю, получаем в итоге следующую зависимость : :

демонстрирующую асимптотическое стремление к стационарному состоянию, тем более медленное, чем больше постоянная времени > Если бы мы заменили индуктивность конденсатором, то аналогичная зависимость получилась бы для напряжения на конденсаторе либо для заряда обкладок, а ток в цепи экспоненциально стремился бы к нулю. В этом случае постоянная времени

вэкспонентах равна %. Предлагаем читателю самостоятельно

вэтом убедиться.

8.2. Колебательный контур

Подробное рассмотрение свойств колебательного контура еще предстоит в следующем разделе нашего курса, но и в курсе электродинамики невозможно оставить без внимания этот фундаментальный объект. Электрическая схема колебательного контура представлена на рис. 8.2. При этом подразумевается, что в сопротивление включены не только резистивные элементы схемы (если они вообще существуют), но и «паразитное» сопротивление катушки индуктивности и соединительных проводов. При последовательном соединении элементов контура такое

306 Квазистационарное электромагнитное поле [ Гл. 8

объединение вполне корректно. Равным образом «паразитная» емкость катушки включена в %.

Вывод уравнения колебательного контура полезно предварить следующим замечанием. Если в схему включен источник ЭДС, то его можно включить в закон Ома или

(Мы учли, что заряд на обкладках и ток в контуре связаны

ние (8.6), но уже для тока, C : Таким образом, динамика контура в любом случае описывается дифференциальным уравнением второго порядка

где — переменная величина (например, C, :), Æ 2+ ,

0 1 +% .

Уравнение (8.8) представляет собой линейное дифференциальное уравнение второго порядка. Известны методы получения его решения; последнее в общем случае зависит от двух произвольных констант. В конкретной физической задаче эти константы доопределяются через начальные условия. Ввиду исключительной важности «колебательной» терминологии и понятийной системы для всего курса физики, мы уделим особое внимание свойствам решений уравнения (8.8).

Начнем с предельного случая нулевой диссипации 0

Æ 0

Уравнение (8.8) в этом случае вырождается в простое уравнение гармонических колебаний, решение которого, включающее произвольные константы , или , , может быть представлено одной из следующих эквивалентных форм:

0 0 ; 0 ;

8.2 ] Колебательный контур 307

Эквивалентность последнего выражения трем предыдущим обусловлена известными соотношениями — формулами Эйлера:

D#

Такое представление осциллирующих функций экспонентами от мнимого аргумента, как мы вскоре убедимся, есть наиболее конструктивный метод описания волновых и колебательных про-

цессов.

Коэффициенты , называются амплитудными, а величина , «сдвигающая» начало отсчета времени, именуется фазой; фазой называют также и полный аргумент осциллирующих

функций 0 Решение полного уравнения (8.8) отличается от этих чисто

гармонических функций лишь учетом диссипации. В самом общем виде оно содержит две произвольные константы и может

В случае достаточно слабой диссипации решения (8.9) не должны сильно отличаться от чисто колебательных. Тогда корни 81,2 оказываются комплексными величинами, так что мы можем, используя формулы Эйлера, записать решение в эквивалентной форме:

случае оно представляет собой монотонно затухающую функ-

цию, которую лучше всего представлять именно в виде (8.9). Величина Æ 2+ называется декрементом затухания; по

физическому смыслу это обратное время затухания колебаний в D 2,718 раз. Если Æ 0, колебания можно считать почти периодическими, подобно приведенным выше решениям для уравнения гармонических колебаний. Это неравенство удобно переписать как условие для характерных времен:

При этом 0 При условии (8.12) корни уравнения (8.10) оказываются непременно комплексными, а с ними и решения (8.9).

Надлежащим выбором констант интегрирования они «привязываются» к вещественным начальным условиям; соответственно, решение (8.11) представлено в формально вещественном виде. Но такое представление оказывается не слишком удобным. Применяя к той или иной осциллирующей функции линейные операции дифференцирования либо интегрирования, мы всегда вынуждены будем превращать sin в cos и наоборот, да еще и с учетом знака; дополнительно усложняет как процедуру, так и ответ экспонента, модулирующая в (8.11) тригонометрическую функцию. Намного проще та же операция с чисто экспоненциальными функциями типа (8.9). Экспонента при дифференцировании или интегрировании просто умножается на постоянный множитель, каждый раз один и тот же. С другой стороны, как мы уже видели, cos представляет собой функционально вещественную часть экспоненты (а sin — мнимую), поэтому в линейной задаче (пока решения не приходится перемножать, возводить в степень и т. д.) их нетрудно поставить во взаимно однозначное соответствие. Таким образом, решение типового уравнения (8.8) ищется в виде

а затем физические величины (:, ,) получают, взяв от него только вещественную или только мнимую часть. Чаще всего в этом даже нет необходимости, поскольку амплитуда и фаза, определенные из начальных условий, полностью описывают колебательный процесс.

При дифференцировании решения (8.13) последнее просто умножается на Æ , при интегрировании — делится на ту же величину. Из соотношения

D 2

следует, что при умножении или делении на мнимую единицу полная фаза меняется на $ 2 — это как раз и соответствует переходу синуса в косинус и наоборот.

При необходимости работать с квадратичными величинами (как-то энергия колебаний) представление (8.13) уже не годится, но экспоненциальную форму решения можно сохранить, заменив (8.13) следующим — уже вполне точным — решением:

J 12 ,

где звездочка — знак комплексного сопряжения. Подобно тому, как у механического маятника сумма потенциальной и кинетической энергий есть величина постоянная (в пренебрежении диссипацией!), а средние их значения по периоду равны, для колебательного контура при Æ 0 имеют место следующие

8.3 ] Вынужденные колебания. Переменный ток 309

соотношения:

Читателю предлагается самому убедиться в справедливости (8.14); заметим, что, помимо данного выше рецепта, можно пользоваться и тригонометрическим представлением (8.11) вместе с известными свойствами средних:

используется величина, именуемая в теории колебаний добротностью (обозначение — C, от английского quality). По

определению

В любой из этих формул подразумевается, что добротность — характеристика колебательного контура. На самом деле это понятие гораздо шире, а потому мы приведем его к более универсальному виду. Пусть ) — запас энергии в контуре. Оценим потери энергии за период, считая диссипацию слабой: Æ

) ) 1 D 2Æ 1 ) 2Æ 2>9

Таким образом, добротность, с точностью до коэффициента — это обратное отношение энергии, запасенной в колебательной системе, к ее потерям за период:

8.3. Вынужденные колебания. Переменный ток

Из проведенного выше рассмотрения переходных процессов — формулы (8.3)–(8.5) — следует, что емкостные и индуктивные элементы можно включать в цепь так, как если бы это были сопротивления, но, в отличие от последних, падение напряжения на них в зависимости от тока задается не умножением, а другими линейными операциями:

Поэтому, например, для случая гармонической функции : падение напряжения на конденсаторе или катушке индуктивности, помимо амплитудного коэффициента, характеризуется также фа-

зовым сдвигом $ 2. Такие элементы называются реактивными, в отличие от активного элемента — сопротивления.

(Строго говоря, любой соленоид, если только он не сверхпроводящий, обладает активным сопротивлением, так что и сдвиг фаз оказывается меньше $ 2.) Главное свойство чисто реактивного элемента состоит в том, что синусоидальный ток проходит его без энергетических потерь. В самом деле, подсчитаем выделение энергии в среднем за период:

В общем случае синусоидальных тока и напряжения, сдвинутых по фазе на :

: :0 ; , ,0 ,

среднее энерговыделение равно

#

Нетрудно заметить, что знак сдвига фазы не имеет значения. Это вполне физично, поскольку «опережение» или «отставание» по фазе суть понятия условные и зависят, например, от принятого в определении (8.13) знака частоты. Так же легко понять, что, пока и поскольку мы не включаем явно в нашу цепь динамомашину, ограничиваясь пассивными элементами , +, %, сдвиг фазы не может превышать $ 2, точнее, при произвольном определении момента включения, он обязан принадлежать интервалу2 1 2 $; 2 1 2 $ , где — любое натуральное число. В противном случае энергия в цепи не рассеивалась бы, а порождалась.

В частном случае активного сопротивления (8.18) дает

Это соотношение принято привязывать к формуле (3.13) и таким образом определять эффективное напряжение сети; например, стандартному напряжению ,эф 220 В соответствует амплитуда

синусоидального напряжения ,0 2,эф2 311 В. Так же опре-