
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf7.2 ] |
Диполь в магнитном поле |
291 |
(Только условия «точечности» будут различны — в одном случае необходимо с надлежащей точностью обеспечить квазинейтральность div 0, а в другом — неразрывность токов div 0.)
Мы воспользуемся этим обстоятельством, чтобы избежать весьма трудоемкого вывода из определения (4.21) формул, аналогичных (1.27) и (1.28), а вместо этого сразу же воспроизведем их с соответствующими переобозначениями:
, |
(7.4) |
|
(7.5) |
Как известно из механики, консервативные силы |
связаны |
с потенциальной энергией соотношением |
в од- |
номерном случае, а в трехмерном мы должны повторить то же самое для , , так что ) — мы уже использовали это обстоятельство в электростатике. Таким образом, (7.4) может быть представлена в эквивалентном виде: энергия магнитного диполя во внешнем поле равна
) |
(7.6) |
Это соотношение является базовым для определения единицы дипольного момента — он измеряется в джоулях на тесла
(Дж/Тл). Мы уже использовали эту единицу в гл. 5 для магнетона Бора.
Если бы речь шла только о заданном диполе — например постоянном магните малого размера, формулами (7.4) и (7.6) можно было бы и ограничиться, но в случае, когда мы имеем дело с наведенным дипольным моментом, в них неявно заключена опасность ошибки. Именно, если или вообще дипольный момент функционально как-то связан с полем, возникает вопрос, следует ли и его дифференцировать в (7.4). Правильно будет этого не делать, потому что взаимодействие диполя с полем — характеристика силовая, и она не может зависеть от природы диполя: на диполи с одинаковыми дипольными моментами должна действовать одинаковая сила безотносительно к их происхождению. В таких случаях принято указывать в формуле, на какой именно сомножитель действует оператор :
" ,
но лучше привести (7.4) к такому виду, в котором m заведомо не дифференцируется. Воспользуемся векторным тождеством
, rot " ,
которое позволяет записать силу (7.4) в следующем виде:
" , rot |
(7.7) |
10*
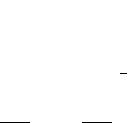
292 |
Энергия и силы в магнитном поле |
[ Гл. 7 |
|
В магнитоактивном веществе соотношение (7.7) естественно |
|
представить в форме объемной плотности силы |
|
|
|
, rot |
(7.8) |
В соответствии с вышесказанным, величина J(r) здесь не дифференцируется.
Дальнейшее преобразование формулы (7.8) требует явного учета зависимости J(B). Мы ограничимся простым случаем линейной связи, т. е. диаили парамагнетиками:
10 1 ! 1
!!0
Подставим это выражение в (7.8) и проведем векторное преобразование, аналогичное тому, что мы сделали при выводе (7.3):
, rot 12 2
В итоге получаем
|
! 1 2 ! 1 |
(7.9) |
|
2!!0 |
2 |
||
Мы снова выразили силу, распределенную в среде, в форме градиента давления (7.2). Но этот результат еще может быть дополнен плотностью силы Ампера (7.3), если магнетик одновременно является проводником. Особенно интересно отметить, что эффективное «давление»
« » ! 1 |
|
(7.10) |
2 |
|
|
может быть как положительным при 1 ' 1, так и отрицательным при 1 & 1. Как следствие, диамагнетик выталкивается из области более сильного магнитного поля, а парамагнетик, напротив, втягивается в нее. Этот эффект может быть с успехом продемонстрирован на примере растворов параили диамагнитных солей. По существу, мы получили объяснение и того общеизвестного факта, что предметы из магнитомягкого железа притягиваются постоянным магнитом. Конечно, конкретные формулы (7.9), (7.10) могут оказаться неадекватными из-за нелинейности зависимости J(B), но качественно это тот же самый эффект. (Что касается магнитотвердых материалов, то здесь может оказаться существенной их собственная намагниченность.)
7.3. Энергия магнитного поля
Понятие энергии магнитного поля можно ввести, следуя программе, изложенной в гл. 2: оперируя экспериментальной информацией о свойствах магнитного поля, предложить такой мыслен-
7.3 ] Энергия магнитного поля 293
ный эксперимент, в котором появился бы интеграл движения, включающий аддитивно механическую энергию и в отсутствие магнитного поля к ней сводящийся. Тогда добавка, обусловленная магнитным полем, и должна трактоваться как магнитная энергия.
Невозможно, однако, предложить один мысленный эксперимент на все случаи жизни. Поэтому новое понятие неизбежно проверяется снова и снова по мере накопления экспериментального материала, иногда дополняется или модифицируется. В конечном счете все принципиальные моменты в физике оказываются — пусть даже косвенно — экспериментального происхождения.
В данном случае особенно деликатным оказывается вопрос о магнитном поле в веществе, поскольку не всегда просто разделить энергию поля, энергию вещества и энергию взаимодействия поля с веществом.
Хотя мы уже обсуждали подобного рода вопросы в гл. 2, это краткое введение представляется все же не лишним. А теперь поставим первый мысленный эксперимент. Обратимся к рис. 7.2 а.
Представим |
себе |
тонкий |
|
|
|
бесконечно длинный идеально |
B |
B |
|||
проводящий |
цилиндр |
(его |
|
|
|
обычно называют лайнером), |
|
|
|||
по которому течет однородный |
i |
|
|||
азимутальный ток с посто- |
|
||||
|
|
||||
янной линейной плотностью. |
|
|
|||
Внутри цилиндр пуст; ника- |
|
|
|||
ких источников энергии либо |
|
|
|||
каналов диссипации в задаче |
à |
á |
|||
нет. Представим далее, что мы |
|||||
|
Рис. 7.2 |
||||
сжимаем лайнер, прикладывая |
|
||||
извне давление . При сжатии от начального радиуса на совершается следующая работа на единицу длины:
Æ 2$
Пусть смещение происходит очень медленно, практически без ускорения, и пусть мы можем пренебречь всеми механическими напряжениями в веществе лайнера. Заметим, что ввиду высокой степени симметрии, магнитное поле вне лайнера — в точности равно нулю, а внутри него оно совершенно однородно и силовые линии параллельны оси. В этой ситуации совершенно неважно, как именно распределен ток по глубине оболочки — все равно имеет место механическое равновесие: 2
Последующие вычисления будут базироваться на законе Фарадея в его самой простой формулировке: магнитный поток через любой идеально проводящий контур — инвариант. В нашей
294 |
Энергия и силы в магнитном поле |
[ Гл. 7 |
постановке задачи это значит, что инвариантным является произведение поля на площадь поперечного сечения лайнера, т. е., G 2. Тем самым 4, и мы можем через механическую работу определить энергию поля внутри лайнера. Удобно сопоставить работу против сил магнитного давления при сжатии лайнера от бесконечного до текущего радиуса с энергией поля на единицу длины лайнера:
> |
|
1 |
G 2$ |
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
4 |
2 $ 2 1 |
|
||
|
|
|
$ G |
|
|
|
G |
|
|
|
# |
2 |
|||
Мы получили энергию в форме, уже привычной нам из электро-
статики. Исходя из этого модельного результата, можно предложить следующее выражение для плотности магнитной энергии:
= , (7.11)
2
которое и подтверждается всем опытом современной электродинамики. Мы получили его сразу в наиболее универсальном виде, который можно будет переносить непосредственно на поле
ввеществе.
Всамом деле, мысленный эксперимент станет еще более фантастичным, но не менее корректным, если мы заполним лайнер некоторой идеально сжимаемой магнитоактивной средой, а
врезультате получится то же выражение (7.11) для плотности энергии магнитного поля, но теперь уже 10 .
Вкачестве следующего объекта для рассуждений возьмем изображенный на рис. 7.2 б бесконечно длинный идеально проводящий соленоид с плотной намоткой (число витков на единицу
длины ! 1, где — радиус соленоида, — его длина). По обмотке соленоида течет ток :, при этом G :, внутри соленоид заполнен сердечником из однородного магнетика. Считается, что зависимость G известна; она, в частности, может быть и линейной 101G, что несколько упрощает конечные формулы.
Энергия магнитного поля на единицу длины соленоида
> |
|
|
|
$ |
2 1 |
0:, |
|
|
|
|
|
|
|||
|
2 |
2 |
|||||
где 0 — поток магнитной индукции через отдельный виток; рассматривая соленоид как целое, учтем, что полный магнитный поток через его обмотку есть ! 0, а полная энергия катушки

7.3 ] Энергия магнитного поля 295
(контура) с током может быть представлена в виде |
|
||
) |
+ |
|
(7.12) |
|
|||
2 |
|
|
|
Мы снова отдали предпочтение универсальной форме записи, наименее чувствительной к деталям постановки задачи. Но для очень широкого класса контуров без сердечника или с магнитомягким сердечником формулу (7.12) можно заменить более конкретной, предполагающей линейную зависимость G :
+:; ) + |
2 |
, |
где + $101 2 $101 |
B 2 |
|
|
2 |
|
|
|
|
(7.13) |
|
|
|
|
|
|
||
Коэффициент + — не что иное, как индуктивность соленоида. Она зависит, как нам уже известно, только от геометрии контура и магнитной проницаемости вещества сердечника (если таковой имеется).
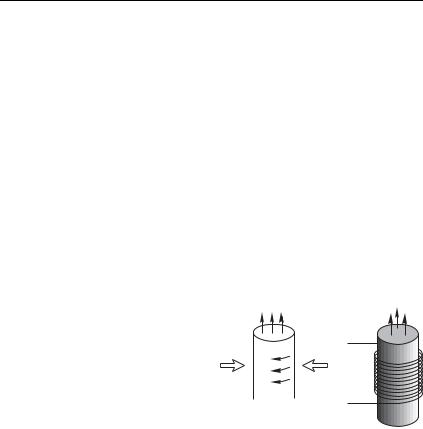
Проведенное выше вычисление энергии катушки с током и введенное понятие индуктивности требуют одной важной оговорки. Мы уже отметили в связи с выводом формулы (4.13), что поле вне бесконечного соленоида — отнюдь не нулевое, а с хорошей точностью — поле прямого тока Gвн : 2$ . Сравним энергию поля в соленоиде, например, (7.13), с энергией внешнего поля. Мы немедленно сталкиваемся с парадоксом: хотя Gвн :, что обеспечено неравенством 1, энергия внешнего поля
оказывается формально бесконечной (интеграл |
G2 |
вн 2$ |
расходится логарифмически). В зависимости от геометрии системы, возможны два выхода из
этой ситуации. |
|
Râí |
|
||||
1. Пусть вся электрическая цепь |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
достаточно симметрична. На рис. 7.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
представлен модельный пример пол- |
|
|
|
|
|
|
|
R |
|
|
|||||
ной аксиальной симметрии. Соленоид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
радиуса включен последовательно |
|
Рис. 7.3 |
|
||||
с источником; цепь замкнута внеш- |
|
|
|
|
|
|
|
ним цилиндрическим токопроводом радиуса вн, соосным с соленоидом. В этом случае справедливость результатов (7.12), (7.13) можно обеспечить следующим сильным неравенством:
вн |
|
G $ 2 10 Gвн2 |
2$ |
|
|
Подставляя G : , Gвн : и опуская, ввиду сильного неравенства, коэффициенты порядка единицы, получим
2 вн
1

296 Энергия и силы в магнитном поле [ Гл. 7
(Читатель может проверить этот результат в качестве упражнения.)
2. Если, напротив, электрическая цепь совершенно не симметрична, то на больших расстояниях поле ее будет зависеть от координат примерно как поле диполя Gвн 3, так что на самом деле интеграл энергии сходится при учете реальной трехмерности задачи. Но характерный пространственный масштаб спадания поля в общем случае не определен, так что для уверенности в правильности формулы (7.13) его следует приравнять максимально возможному — длине соленоида . Отсюда следует
оценка
2 2
1 ,
т. е. в обоих случаях условие на плотность намотки оказывается несколько более жестким, чем предполагалось вначале.
Такого рода соотношения приходится постоянно держать
вполе зрения при работе с сильноточными системами. Мы хотим
вданном случае обратить внимание на ограниченную применимость хрестоматийных формул (7.13), но это никоим образом не ставит под сомнение общий результат (7.11), да и формула (7.12)
при правильном вычислении потока через полный контур (а не только соленоид) остается в силе.
Дадим формальный вывод выражения для плотности энергии (7.11), базирующийся на аксиоматическом представлении о потенциальной энергии произвольной токовой конфигурации. Известному представлению энергии электрического поля
)эл 12 3
поставим в соответствие в качестве энергии магнитного поля следующее выражение:
)м |
1 |
, |
|
1 |
|
, rot , |
(7.14) |
|
2 |
2 |
|
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
где интегралы берутся по объему всех входящих в систему проводников. Мы распространим интегрирование на все пространство; это не меняет результата, потому что вне проводников0. При этом потенциальная функция должна порождать, в отличие от вектор-потенциала (4.15), действующее поле в веществе , так что, в соответствии с выводом макроскопических уравнений поля в 5.1,
!0 |
" |
микро |
(7.15) |
||||
|
|
|
|
|
" |
|
|
4 |
|
|
|||||
7.3 ] |
Энергия магнитного поля |
297 |
Для дальнейших выкладок нам понадобится следующая цепочка преобразований:
, " , , " rot rot ,
с учетом которых (7.14) можно переписать в виде
)м |
1 |
|
, rot |
|
1 |
, |
|
1 |
|
rot |
|
2 |
2 |
2 |
|||||||||
|
|
|
|
|
|
||||||
Но теперь мы можем первый из интегралов в правой части преобразовать с помощью теоремы Гаусса в поток вектора , через бесконечно удаленную поверхность. Поскольку магнитное поле должно убывать как дипольное или быстрее, на бесконечности G 3, 2, 9 2, так что этот интеграл равен нулю. Таким образом,
)м |
1 |
|
rot |
, |
(7.16) |
|
2 |
||||||
|
|
2 |
|
|||
что эквивалентно выражению (7.11). Тем самым мы фактически продемонстрировали, что энергия магнитного поля может быть, помимо прочего, представлена в виде (7.14), (7.15). Убедившись таким образом в правильности (7.14), попробуем дать вывод соотношений (7.12), (7.13), базирующийся уже не на отдельном частном примере, а на общем законе. Для простоты ограничимся случаем контура без сердечника; обобщения принципиальной трудности не составят, но потребуют более громоздких вычислений. В «вакуумном» случае 10 . Как и при выводе базовых выражений для индуктивных коэффициентов (6.3), (6.4), будем считать контур тонким. Тогда в интегралах (7.14), (7.15)
: , что позволяет переписать их в виде
) !0 |
!0 |
!0++ |
(7.17) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
8 |
8 |
|||||||
|
|
|
|||||||||
Далее ответ зависит от того, что мы понимаем под штрихованными величинами в (7.17). Если имеется в виду всего один контур, то мы получаем просто формулу (7.13), где индуктивность задается выражением (6.4), а если контуров два, то нам придется составить все комбинации, проистекающие от суммирования во всем пространстве j и , A и :
) |
1 |
2 |
2 |
2+12:1:2 |
(7.18) |
|
|
+1:1 +2:2 |
|||||
2 |
||||||
|
|
|
|
|
||
(мы учли, что +12 +21). В случае многих контуров, вводя обозначение + + , можем привести (7.18) к универсальному виду:
) |
1 |
+ : : |
(7.19) |
|
2 |
||||
|
|
|
,
298 Энергия и силы в магнитном поле [ Гл. 7
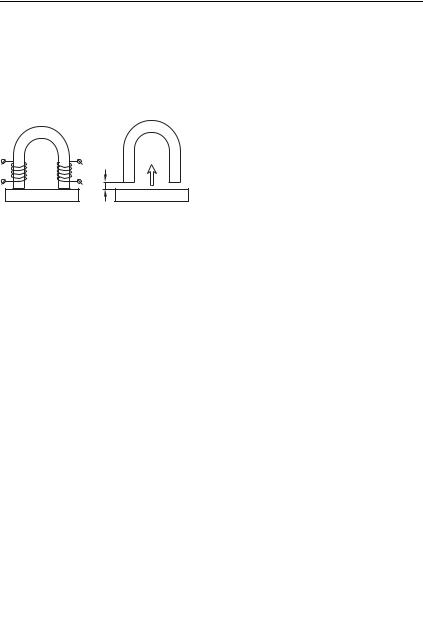
7.4. Подъемная сила электромагнита
Темой данного параграфа будет элементарный расчет подъемной силы электромагнита с сердечником из мягкого железа. Для определенности рассмотрим электромагнит типа простого ярма (рис. 7.4 а). Сечение ярма и якоря 9 будем считать везде одинаковым и настолько малым,
|
|
чтобы имело смысл пользоваться |
|
|
|
приближением однородной маг- |
|
|
F |
нитной цепи. Пусть магнитная |
|
|
|
проницаемость сердечника и яко- |
|
x |
|
ря равна 1 1, длина по обхо- |
|
C |
C |
ду (характерная длина силовой |
|
линии) , число витков обмотки |
|||
à |
á |
||
!, ток через обмотку : (детали |
|||
Рис. 7.4 |
|
||
|
геометрии сердечника и обмотки |
при 1 1 и 91 2 не имеют значения. Подчеркнем, что наша цель — не инженерный расчет, а установление на простейшем примере общих принципов рассмотрения таких систем.
В данном случае мы не можем пользоваться на только результатом (7.10), но и самой идеей его получения. Причина в том, что электромагнит — система динамическая, и корректное ее рассмотрение должно включать источник тока. Припишем последнему ЭДС , а обмоткам — сопротивление .
Для рассмотрения таких систем весьма продуктивен принцип виртуальных перемещений, который мы уже использовали в решении задачи 2 гл. 2. Оторвем якорь от ярма, отодвинув его на расстояние (рис. 7.4 б) и подсчитаем, какая при этом должна быть совершена механическая работа. Полный энергетический баланс выглядит следующим образом:
|
Æ Æ , |
где Æ |
— работа источника ЭДС; Æ — приращение джоулева |
тепла; |
— приращение магнитной энергии контура. |
Величины Æ и Æ должны вычисляться за время перемещения на фоне постоянной мощности, потребляемой электромагнитом. Введем в рассмотрение также приращения тока в контуре и магнитного потока через сердечник в момент перемещения. Эти два приращения должны быть связаны законом Ома и
законом Фарадея:
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приращение работы источника равно |
|
|
|
|
|
|
|
||||
Æ : |
|
: |
|
|
|
|
|
|
: |
||
|
|||||||||||
|
|
|
|
|
|
|
|
||||

7.4 ] |
Подъемная сила электромагнита |
299 |
Приращение джоулевых потерь относительно таковых в стационарном режиме
Æ |
|
: 2 :2 2: |
2: |
И, наконец, приращение энергии магнитного поля, в отличие от диссипативных величин Æ и Æ , определяется только начальным и конечным состояниями:
|
|
+2 |
|
1 |
: |
2 |
1 |
: |
|
|
2 |
2 |
|
|
2 |
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Последняя цепочка равенств заслуживает особого внимания. Во-первых, при дифференцировании энергии поля мы положили0, поскольку она при изменении конфигурации зависит лишь от положения якоря при установившемся токе :0 . (Напротив, приращение тепловыделения и дополнительная работа источника обусловлены как раз приращением тока в контуре в процессе перемещения.) Во-вторых, величина формально совпадает с последующим ответом и потому иногда предлагается в качестве его обоснования. Как рецепт такой прием вполне допустим, но необходимо понимать, что за ним не стоит иного
содержания, кроме проделанных выше выкладок. Итак,
|
1 |
: |
+2 |
|
|
> |
|
(7.20) |
2 |
|
|
||||||
Далее для вычисления |
заменим |
|
малой, но конечной |
|||||
величиной и воспользуемся магнитной цепью с учетом того обстоятельства, что поток через контур в ! раз больше потока через сердечник:
|
|
B+ B |
1019 |
B2+ |
|
|
2! |
||||
|
!0 |
!( 2 !0( |
|
|
Максимальной величине — подъемной силе — соответствует предел 0:
|
+ |
|
!B+ |
2 |
(7.21) |
2 0 |
109 |
|
|
В заключение зададимся вопросом общего характера. Если сила Лоренца принципиально перпендикулярна скорости любой заряженной частицы, как вообще может совершаться работа при проникновении поля в вещество? Чему соответствует потенциальная энергия магнитоактивной среды?
Разрешение этого парадокса состоит в непременном учете эффектов электромагнитной индукции. При любой перестройке поля изменение магнитной индукции . . порождает электрическое поле E, и работу совершает именно это поле. Но сценарий перестройки не входит в ответ, и конечные результаты оказываются универсальными, что и позволяет в очередной раз расширить формулировку закона сохранения энергии.

300 Энергия и силы в магнитном поле [ Гл. 7
Задачи
1. Вдоль равновесного цилиндрического электронейтрального плазменного шнура (пинча) течет ток + (рис. 7.5). Определить температуру на оси пинча, считая температуру на его границе пренебрежимо малой.
z |
Плотность тока и концентрация частиц плазмы однородны |
|
по сечению, причем известно число частиц на единицу |
B |
длины B. |
Решение. Условие равновесия плазменного шнура — |
|
|
баланс силы Ампера и архимедовой силы. В плазме, как |
|
и в газе, давление можно выразить через концентрацию |
|
частиц и абсолютную температуру: Б , где Б — |
|
постоянная Больцмана. Таким образом, плотность архиме- |
jдовой силы в нашей осесимметричной системе можно представить в виде
Рис. 7.5 |
|
|
Б 2 Б # |
Плотность силы Ампера также имеет только радиальную компоненту:
2 3 3
Поле при однородном распределении тока определяется с помощью теоремы о циркуляции (см. задачу 1 гл. 4): 1 2 !03 #. Из баланса сил следует
|
!0 32 |
|
|||
|
|
|
|
|
# |
# |
2 |
Б |
|||
Интегрируя это уравнение, получаем # #2 , причем из условия
0 на внешней границе пинча следует 2, где — радиус плазменного шнура. Вблизи его оси (# 0) получаем ответ
0 !0 32 2 , 4 Б
который приобретает окончательный вид после подстановки 3 +2,
B 2
0 |
!0 |
+2 |
|
(7.22) |
|
4 |
|
Б B |
|||
|
|
|
|
||
|
|
|
|
|
|
Формула (7.22) в магнитной гидродинамике называется по имени английского физика А. Беннета (1750–1799) условием Беннета. Интересно отметить,
что при попытке решить задачу, приравнивая константе сумму газокинетического и магнитного давлений, мы получили бы результат, отличающийся от (7.22) в два раза — это как раз тот случай, когда в выражении для силы (7.3) нельзя пренебречь «натяжением силовых линий».
2. В результате некоторого космического события образовалась система, состоящая из звезды (масса 0, магнитный момент 0) и планеты (масса0, магнитный момент m). Планета движется по круговой орбите радиуса . Найти возможный разброс величины периода обращения в зависимости от ориентации магнитных моментов, считая плоскость орбиты перпендикуляр-
ной 0.
Решение. Добавочная сила, действующая между диполями, может быть представлена в форме (7.4): !0 , где H — поле диполя, которое дается формулой (4.24). В нашем случае вычисления существенно упрощаются, поскольку максимальные поправки к периоду обращения с очевидностью соот-
