2947

лельных рёбер. Наименьшая из длин циклов именуется его

обхватом.

Граф именуется связным, когда всякие две его разные вершины соединены маршрутом.

Путь – это ориентированный маршрут.

Орграф именуется сильно связным, когда для каждых двух вершин xi , xj S имеется путь с началом в xi и концом

в x j . Для неориентированного графа термины путь и мар-

связаны, а вершины из разных Si не связаны. В этом случае

G Gi Si ,Ui . Данное разложение именуется прямым, а

i

указанные подграфы – компонентами связности графа G. Теорема 1. Каждый граф можно представить в виде

обьединения непересекающихся связных компонент. Разложение графа на связные компоненты единственно.

Пример. Разложение орграфа на три сильно связные

при этом возможно равенство как в левой, так и в правой частях.

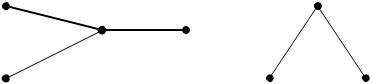
Пример. Проверим выполнение условия (27) для графа G, представленного на рис. 21. У него семь вершин, шесть рёбер и две компоненты связности. Таким образом, в данном

случае n 7, k 2, m G 6. 7 2 5 6 C2 6 5 15.

6 2

Неравенство (27) выполнено.

82

X2

X7

X5

Рис. 21. Граф с двумя компонентами связности

В разных прикладных задачах теории графов дугам графов, отображающих действительные процессы, как правило, приписываются некоторые числовые характеристики. В частности, когда дуги соответствуют расположению станков, на каждом из которых деталь подвергается обработке в результате некоторой операции, числовой характеристикой дуги разумно считать время выполнения соответствующей операции. Можно привести другие аналогичные примеры. При этом говорят, что дугам графа сопоставлены некоторые веса.

Допустим, что дан орграф G S,U . При условии, что любой его дуге xi , xj U приписано определённое число

xi , xj , граф G именуется графом со взвешенными дугами,

Термины «сеть» и «вес маршрута» для неориентированного графа вводятся точно также.

Граф, имеющий только одну вершину, называется три-

виальным.

83

Связностью G графа G называется минимальное

количество вершин, в результате отбрасывания которых получается несвязный или тривиальный граф.

нимальное количество рёбер, в результате отбрасывания которых получается несвязный или тривиальный граф, для ко-

торого G 0.

Простые цепи именуются рёберно-непересекающимися

при условии, что никакие две из них не содержат общего ребра. Если же у таких цепей отсутствуют и общие вершины, то они именуются вершинно непересекающимися.

Допустим, что G – связный граф, а u, v – две разные его вершины. Множество рёбер U графа именуется u, v –

разделяющим множеством в G при условии, что каждая простая цепь из u в v включает ребро из U. Множество вершин S графа, не включающее u, v, именуется u, v – отде-

ляющим множеством в G при условии, что каждая простая цепь из u в v проходит через вершину из S.

нимальному количеству вершин, отделяющих V и V .

Множество вершин именуется внутренне устойчивым, когда все его вершины попарно не соседние.

Внутренне устойчивое множество вершин именуется пустым подграфом, когда в итоге прибавления как минимум одной вершины, не входящей в данное множество, получается как минимум одно ребро (дуга).

84

Наибольшее кардинальное число пустого подграфа гра-

фа G именуется числом внутренней устойчивости, другими словами, вершинным числом независимости графа

Наибольшее количество попарно несмежных рёбер гра-

фа G именуется рёберным числом независимости графа

1 G .

В том случае, когда ребро инцидентно вершине, говорят, что они покрывают друг друга.

Совокупность вершин, покрывающих все рёбра графа

G, именуется вершинным покрытием графа.

Наименьшее кардинальное число вершинного покрытия именуется числом вершинного покрытия графа 0 G .

Подобным образом, множество рёбер, покрывающих все вершины графа G, именуется рёберным покрытием гра-

фа.

Наименьшее кардинальное число рёберного покрытия именуется числом рёберного покрытия графа 1 G .

Теорема. Для каждого нетривиального связного графа

Определение. В том случае, когда любое ребро графа G содержится в одной из имеющихся рёбернонепересекающихся цепей данного графа, то говорят, что множество таких цепей покрывает граф G.

Теорема о минимальном числе рёберно-непересекающихся цепей

В том случае, когда связный граф имеет ровно k вершин нечётной степени, наименьшее количество покрывающих его рёберно-непересекающихся цепей равно k / 2.

Совокупность рёбер графа, в которой ни одна пара рёбер не смежна, именуется паросочетанием графа.

85

Совокупность рёбер паросочетания, в которой количе-

ство рёбер равно 1 , именуется наибольшим паросочетанием графа.

Совершенным паросочетанием из S1 в S2 в двудольном графе G S1, S2 именуется взаимно однозначное соответствие между вершинами из S1 и подмножеством вершин из S2 , такое, что любая вершина из S1 соединена ребром с некоторой вершиной из S2 .

Теорема Холла. Предположим, что G S1, S2 – двудольный граф и для всякого подмножества A S1 обозначим через A совокупность тех вершин, заключённых в S2 ,

являющихся соседними, как минимум, с одной вершиной из A. В этом случае совершенное паросочетание из S1 в S2

Способы задания графов: 1) Латинская матрица.

Для ориентации дуг используется порядок букв в их названиях.

B

U7

Рис. 22. Ориентированный граф

86

Рис. 23. Латинская матрица

В том случае, когда граф неориентированный, в латинской матрице просто штрихуют соответствующие клетки в таблице.

2) Матрица смежности вершин.

Представляет собой квадратную матрицу P порядка n, здесь n – количество вершин. Её строки и столбцы отве-

чают вершинам графа. Элементы pij матрицы смежности равны количеству дуг, идущих из вершины i в j. В том слу-

чае, когда орграф не имеет кратных дуг, матрица является двоичной и содержит только нули и единицы.

87

В неориентированном графе в вместе с ребром xi , x j

имеется ребро xj , xi , следовательно, матрица смежности

вершин в этом случае будет симметрической.

Теорема. Для того, чтобы графы были изоморфны, необходимо и достаточно, чтобы матрицы смежности вершин получались друг из друга совместными перестановками строк и столбцов, другими словами, когда вместе с перестановкой i -ой и j -ой строк переставляются i -ый и j -ый столбцы.

Следствие. Ранги матриц смежности вершин изоморфных графов совпадают.

Матрица смежности вершин единственным образом определяет структуру графа.

Определение. Рангом графа именуется ранг его матрицы смежности вершин. Принята запись: rang G.

3) Матрица смежности дуг.

Представляет квадратную матрица Q порядка m, где m – количество дуг. Элементы qij данной матрицы равны единице при условии, что дуга ui входит в дугу u j и равны нулю в других случаях. Для неориентированного графа эле-

Это матрица смежности дуг для графа на рис. 22, в котором удалена петля u9 .

4) Матрица инциденций.

Представляет собой прямоугольную матрица R размерности n m, здесь m – количество дуг, а n – количество

вершину; 0, когда дуга не инцидентна i -ой вершине. Для неориентированного графа элементами матрицы являются чис-

Строки матрицы инциденций именуются векторами ин-

циденций графа G.

Теорема. Для того, чтобы графы были изоморфны, необходимо и достаточно, чтобы их матрицы инциденций получались друг из друга произвольными перестановками строк и столбцов.

Матрица инциденций тоже единственным образом определяет структуру графа.

5) Матрица весов – матрица ij , здесь ij – вес ребра, соединяющего вершины xi и x j . Веса несуществующих рёбер считаются равными нулю или бесконечности в за-

89

висимости от приложений. Матрица весов представляет собой простое обобщение матрицы смежности вершин.

6) Матрица Кирхгофа. Матрица Кирхгофа графа G –

Свойства матрицы Кирхгофа.

1.Суммы элементов в любой строке и любом столбце матрицы B равны нулю.

2.Алгебраические дополнения (в другой терминологии, адъюнкты) всех элементов матрицы B равны между собой.

7) Матрицы связности и достижимости.

Заданы P G – матрица смежности вершин графа

G – неорграф, и матрицей достижимости, когда G – орг-

раф. В матрице C заключена информация о наличии связей между разными элементами графа G с помощью маршрутов.

Теорема. L CT .

Матрицы C и L применяются для выявления компонент сильной связности графа. Положим F C * L, здесь

символ * подразумевает поэлементное умножение матриц C

90