2947

этом компонента сильной связности орграфа, имеющая вершину xi , состоит из вершин x j , для которых fij 1.

Пример.

X2 X3

X6

X1

X4 X5

Рис. 24. Сильно связный орграф

91

92

Рис. 25. Сильно связные компоненты

3.2. Метрические характеристики графа. Упорядочивание вершин и дуг орграфа

Метрические характеристики графа.

Пусть задан связный граф G S,U , x1 и x2 – две его вершины. Длина наименьшего x1, x2 – маршрута именуется

расстоянием между вершинами x1 и x2 , при этом принята

запись: d x1, x2 .

Свойства расстояния между вершинами:

1) Расстояние между вершинами есть длина простой це-

пи.

2) d xi , xi 0.

Для вершины x значение

именуется её эксцентриситетом. Наибольший из всех эксцентриситетов именуется диаметром графа G, при этом

принята запись d G , таким образом,

Наименьший из эксцентриситетов вершин графа именуется его радиусом, при этом принята запись r G .

Вершина x именуется периферийной в том случае, когда её эксцентриситет равен диаметру графа.

Простая цепь, расстояние между концами которой рав-

но d G , называется диаметральной цепью.

Вершина x называется центральной в том случае, когда e x r G . Совокупность всех центральных вершин графа

именуется его центром.

Теорема. Для каждого связного графа G имеет место оценка: d G rang G.

Пример. Найти метрические характеристики графа G , изображённого на рис. 26.

х3

Рис. 26. Неориетированный граф

Решение.

d x1, x1 0, d x1, x2 1, d x1, x3 2, d x1, x4 2, d x1, x5 1, d x1, x6 2, d x1, x7 3;

e x1 max 0,1, 2, 2,1, 2,3 3. 97

Рассуждая подобным образом, получим:

В исходном графе центральной является вершина x5 , она же образует центр графа G, периферийными будут вершины x3 и x7 .

Упорядочивание дуг и вершин орграфа.

Вычисления в задачах теории графов становятся гораздо легче, когда элементы графов упорядочены. Под упорядо-

чиванием вершин связного графа без контуров (другими сло-

вами, циклических цепей) подразумевается разделение его вершин на группы, удовлетворяющее условиям:

1)вершины первой группы не имеют предшествующих вершин, а вершины последней группы последующих;

2)вершины любой другой группы не имеют предшествующих в следующей группе;

3)вершины одной и той же группы дугами не соединя-

ются.

Описанная выше группировка всегда осуществима. В итоге такого процесса строится граф, изоморфный данному.

Алгоритм Фалкерсона.

1.Определить вершины графа, в которые не заходит ни одна дуга. Они образуют первую группу. Присвоить вершинам группы номера в произвольном порядке.

2.Удалить все занумерованные вершины и дуги, из них выходящие. В построенном таким образом графе существует, как минимум, одна вершина, в которую не заходит ни одна дуга. Данной вершине, входящей во вторую группу, приписывают следующий порядковый номер и так далее. Второй

98

шаг повторяют до тех пор, пока не будут упорядочены все вершины.

Подобным образом упорядочиваются дуги орграфа.

1.Ищутся дуги, не имеющие входящих в них дуг. Они войдут в первую группу.

2.Удаляются эти дуги. В новом графе существует, как минимум, одна дуга, не имеющая входящих в неё дуг. Данные дуги войдут во вторую группу. Второй шаг повторяют до тех пор, пока все дуги не будут разделены на группы.

Пример.

B

D C

A

E

Рис. 27. Исходный орграф

1)Вершина B не имеет заходящих в неё дуг, причислим её к первой группе.

2)Удалим все дуги, выходящие из B , в результате обра-

D C

A

E

Рис. 28. Первая операция

99

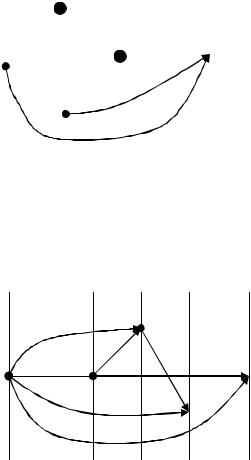
В нём снова ищем вершину, в которую не входит ни одна дуга. Это вершина D . Удаляем дуги, выходящие из D . Имеется ещё одна вершина E , в которую не входит ни одна дуга.

B

D C

A

E

Рис. 29. Вторая операция

После удаления дуг EC и EA останутся вершина A , которая войдёт в четвёртую группу, и вершина C – в пятую.

Получим изоморфный исходному граф с упорядоченными вершинами:

E

B D

Рис. 30. Результат упорядочивания вершин

100