2947

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный

технический университет»

И. М. Пашуева, А. Н. Шелковой, Н. А. Ююкин

ДИСКРЕТНАЯ МАТЕМАТИКА

ВИНФОРМАЦИОННЫХ СИСТЕМАХ

ИТЕХНОЛОГИЯХ

Утверждено учебно-методическим советом университета в качестве учебного пособия

Воронеж 2018

УДК 512.64 ББК 22.143

П225

Рецензенты:

кафедра математики и моделирования систем Воронежского института МВД России

(д-р физ.-мат. наук, проф. В. В. Меньших); канд. физ.-мат. наук, доц. С. П. Майорова

Пашуева, И. М.

Дискретная математика в информационных системах и технологиях: учебное пособие [Электронный ресурс]. –

П225 Электрон. текстовые, граф. данные (2,4 Мб) / И. М. Пашуева, А. Н. Шелковой, Н. А. Ююкин. – Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2018. – 1 электрон. опт. диск (CD-ROM): цв. – Систем. требования: ПК 500 и выше; 256 Мб ОЗУ; Windows XP; SVGA с

разрешением 1024x768; Adobe Acrobat; CD-ROM; мышь. –

Загл. с экрана.

ISBN 978-5-7731-0718-7

В учебном пособии содержатся элементы теории множеств, методы комбинаторики и теории графов.

Издание соответствует требованиям ФГОС ВО по направлению 09.03.02 «Информационные системы и технологии» (все профили), дисциплине «Дискретная математика». Для студентов 1 курса очной формы обучения.

Ил. 75. Табл. 2. Библиогр.: 23 назв.

УДК 512.64 ББК 22.143

ISBN 978-5-7731-0718-7 Пашуева И. М., Шелковой А. Н.,

Ююкин Н. А., 2018

ФГБОУ ВО «Воронежский государственный технический университет», 2018

2

ВВЕДЕНИЕ

Это учебное пособие написано на основе лекций, читаемых одним из авторов на факультете информационных технологий и компьютерной безопасности ВГТУ по курсу «Дискретная математика».

В пособии изложены необходимые основы математического аппарата и примеры его использования в современных информационных приложениях: элементы теории множеств, комбинаторики, теории графов. Такой объём знаний актуален сегодня для студентов, получающих образование по информационным специальностям, и соответствует требованиям государственных стандартов по информационным специальностям.

Изложение материала проведено почти без доказательств – основной упор сделан на приобретение навыков использования математического аппарата. Каждый раздел сопровождается решением характерных задач и соответствующими информационными приложениями. Пособие также содержит подборку вопросов для повторения, задач и упражнений для самостоятельного решения по каждой теме.

3

ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

1.1.Множества и действия над ними

1.1.1. Понятие множества

Множество относится к первичным математическим понятиям, не определяемым через более простые понятия, и вводится аксиоматически (см. п. 4 данной главы). Оно может иметь произвольное количество объектов любой принадлежности, которые являются однородными относительно какогонибудь признака. Эти объекты называются элементами данного множества. Если количество элементов множества конечно, оно называется конечным множеством, в противном случае – бесконечным множеством.

Если x входит в состав элементов множества X , записывают: x X . Словесно это означает, что x принадлежит X . Иначе, если x не относится к элементам множества X , то пишут: x X . Это означает, что x не принадлежит X . Тот факт, что в множество X входят элементы x1, x2 , ..., xn , за-

писывается в виде выражения X x1, x2 , ..., xn .

Примеры множеств: множество деревьев в парке, множество молекул в данном веществе и так далее.

В случае, когда множество не содержит ни одного элемента, оно носит название пустого множества и обозначается символом .

Предположим, что имеются два множества X и Y . При условии, что любой элемент множества X одновременно входит в множество Y , тогда X называется подмножест-

вом множества Y . Этот факт записывается в виде: X Y ( X содержится в Y ) или Y X (Y содержит X ).

Свойства подмножеств.

Пусть дано произвольное множество A . Тогда: 4

1)A A ;

2)A.

Множества A и B называются равными при условии, что они содержат одни и те же элементы. Обозначение:

x x A x B A B.

Любое подмножество A данного множества B , отлич-

ное от B и , называется собственным подмножеством B :

A B. Пустое множество и само множество A называ-

ются несобственными подмножествами A .

Набор всех подмножеств множества A именуется его

булеаном или множеством-степенью (применяются записи

P A или 2A ).

Универсальное множество (универсум) U – множество,

в которое входят в качестве подмножеств все другие множества, которые можно рассматривать, решая конкретную задачу. Выбор универсума неоднозначен, однако если он сделан, таким множеством можно руководствоваться в качестве общего при решении имеющейся задачи.

Примеры.

1) Когда речь ведётся только о цветах и кому-то захотелось поговорить о многих разновидностях цветов, то не нужно высказываться о тополях, и естественно выбрать в роли универсума множество всех цветов.

5

2) Если беседуют о цветах, кустарниках и деревьях, то универсумом разумнее считать всю флору.

Множество, изучаемое одновременно с каким-либо заведённым в нём порядком расположения элементов, называется упорядоченным множеством, при этом применяется запись:x1, x2 , ..., xn . При условии, что a A и b B , пара элемен-

тов a, b называется упорядоченной парой, при этом равен-

подмножество универсального множества U , разность U \ A именуется дополнением множества A, при этом применяется

запись A .

Симметрической разностью (другими словами, коль-

цевой суммой) множеств A и B именуется множество

C A B A B x A x B x A x B .

6

Если множество имеет своими элементами все упорядоченные пары a, b , a A, b B, то оно именуется прямым

(по-другому, декартовым) произведением множеств A и B,

при этом применяется запись: A B. Прямое произведение A A именуется декартовым квадратом, при этом применя-

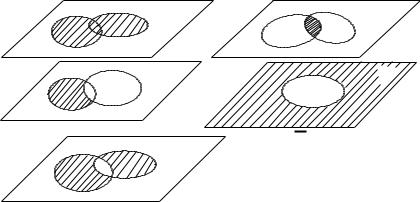
Геометрический смысл действий над множествами состоит в изображении их в виде диаграмм Эйлера-Венна. Если

А В=АВ

Рис. 1. Диаграммы Эйлера-Венна

7

Свойства операций над множествами (законы алгебры множеств).

1) Переместительный закон: A B B A;

A B B A.

2) Сочетательный закон: A B C A B C ;

A B C A B C .

3)Распределительный закон:

A B C A B A C ;

A B C A B A C .

4)Законы идемпотентности: A A A; A A A.

5)Законы поглощения: A A B A;

A A B A.

6) Законы двойственности де Моргана:

А В А В, А В А В.

7)Закон двойного отрицания: A А.

8)Закон включения: А В В А.

9)Закон равенства:

АВ ((А В) (В С) (А В) (А В)).

Разумеется, приведённой выше сводкой число свойств операций над множествами не ограничивается. Иные законы алгебры множеств можно получить, используя свойства 1 – 9.

8

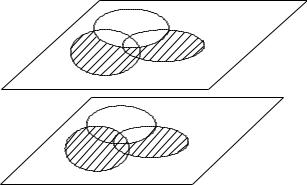
Пример. Доказать соотношение: (А В) \ С А (В \ С).

Доказательство. Проще всего провести, используя диаграммы Эйлера–Венна.

Рис. 2. Графическая интерпретация

1.2. Отношения и функции

Каждое подмножество прямого произведения именуется n -местным отношением (по-

другому, n -местным предикатом) P , заданным на множест-

ется унарным и есть подмножество множества A1 . Бинарным (или двуместным) в случае n 2 отношением именуется совокупность упорядоченных пар. Элементы x1, x2 , ..., xn име-

нуются координатами (по-другому, компонентами) отноше-

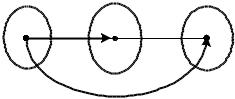
Q B C именуется множество P o Q x, y : x A, y C,

РQ

Рис. 3. Композиция бинарных отношений

Свойства бинарных отношений.

1)P P 1 1 P .

2)P, Q P o Q 1 Q 1 o P 1.

3)( P, Q, R P o Q o R P o Q o R – сочетательный закон для композиции.

10