2616

1

r r

r

Vnp

=

a(b ´c )

=10.

3

5.3. Доказать компланарность векторов

r

r

r

a {4,3,5}, b {2,2,2}, c {-3,-2,-4}

r

r

r

Решение. Условие компланарности

a(b ´c ) = 0. Откуда

r

r

r

4

3

5

2

2

2

= 0,

a(b ´c ) =

- 3 - 2 - 4

следовательно, векторы компланарны.

r

r

= (-1,-1,2) и

5.4. Даны векторы a

b = (1,-2,2). Найти

неизвестный вектор

r

= (x,y,z), если скалярное произведение

x

r

r

вектор

r

r

r

перпендикулярен

оси Ох,

а

a

× x = -7,

c

= a

´ x

смешанное произведение

r r

r

x a b = 2.

Решение.

Используя

r r

= -7,

получим

условие a x

уравнение –x – y+2z = -7

или x + y - 2 z = 7.

Воспользуемся векторным произведением

r

r

r

r

r

r

i

j

k

r

r

r

-1

-1 2

c

= a

´ x =

= -(z + 2 y)i + (2x + z) j + (x - y)k .

x

y

z

r

Поскольку

перпендикулярен

оси Ох,

то

вектор c

проекция cx вектора

r

на ось Ох равна 0, то есть cx =-(2y+z)=0.

c

Из условия

r

r

r

x a b =2 имеем

x

y

z

= 2, т.е. 2x+4y+3z=2.

-1

-1

2

1

- 2

2

Полученные уравнения объединим в систему

ìx + y - 2z = 7,

ï

2 y + z = 0,

í

ï

+ 3z = 2.

î2x + 4 y

Решение

ищем

по

формулам

Крамера. Находим

определитель системы

D =

1

1

- 2

0

2

1

= 12 ¹ 0.

2

4

3

система имеет единственное решение x =

D

x

, y =

Dy

,

z =

D

z

.

7 1 - 2

1 7 - 2

D

D

D

Dx

=

= 24; Dy

=

= 12; Dz

=

1 1 7

= -24.

0

2

1

0

0

1

0

2

0

2

4

3

2

2

3

2

4

2

x =

24

= 2, y =

12

= 1, z =

- 24

= -2.

12

12

12

r

Таким образом, неизвестный вектор

x = {2,1, -2} .

5.5. На векторах

r

r

r

r

r

r

r

r

и

r

r

a = 2i + j - k , b = 3i - 2 j + 4k

r

построен

параллелепипед. Найти

его

высоту,

c = 3i - 4k

опущенную на грань, образованную векторами

r

r

a и b .

Решение. Объем параллелепипеда по формуле (4) будет

r

r

r

r rr

i

j

k

3

- 2

4

=

16 +12 - 6 +12

= 34.

V = (abc ) =

3

0

- 4

С

другой

стороны, объем

равен V = S×h,

где

S –

площадь грани, образованная векторами

r

и

r

a

c .

r

r

r

r

r

i

j

k

r

r

r

S = a

´ c

= 2 1 -1 = - 4i + 5 j - 3k =

Таким образом, H =

V

=

34

=

17 2

.

5 2

S

5

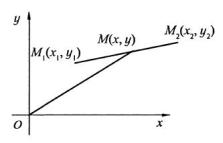
1°. Координатой точки М на

оси х называется

положительное

или

отрицательное

,числоотложенное,

Рис. 3.1

Декартовыми

координатами

точкиМ

называются

проекции радиус-вектора ОМ на оси координат (х, у ).

Направленным отрезком на оси называется отрезок, у

которого

определены

начало М1 (х1 )

и конец М 2 (х2 ) .

Здесь

х1 , х2 - координаты начала и конца отрезка.

2°.

Величина

отрезка

на

оси

равна

его

длин

М1М 2 =

М1М 2

,если направление отрезка совпадает с осью; в

противном случае величина отрезка равна его длине со знаком

минус М1М 2 = -

М 2М1

. Через координаты величина отрезка

определяется по формуле

М1М2 = х2 - х1 ,

(1)

а длина или расстояние между двумя точками

d = М1М 2

=

х2 - х1

.

(2)

Длина отрезка на плоскости(рис. 3.1),

заданного

координатами своего началаМ1 (х1 , у1 )и

конца М 2 (х2 , у2 ),

равна

d =

(x - x )2

+ (y

2

- y )2 .

(3)

2

1

1

Если начало отрезка совпадает с началом координат, то

формула (3) примет вид

d =

x2 + y2

(4)

3°. Пусть j и y

- углы,

составляемые

отрезком с

cosj =

х2 - х1

; cosy =

у2 - у1

2 + у

2 + у

(

х - х

- у

2

(

х - х

- у

2

2 1 )

( 2

1 )

2 1 )

( 2

1 )

cosj =

4 +1

=

1

=

2

; cosy =

2

+ 3

=

2

.

2

2

2

2

5

2

5

Отсюда угол

с положительным направлением осиОх

равен j = 45o , а оси Оу равен y = 45o .

1.3. Найти точку,

удаленную

от осиОу и от точки

Решая последнее уравнение, находим

y1 = 5, у2

= -1.

Таким образом, искомых точек на

прямой

две

2

13

третье,

находим, что

y =

. Подставляя

найденныех,у в

2

любое из трех уравнений, получаем, что R =

130

.

2

1.5. Доказать,

что четырехугольник

с вершинами

в

точках

A (1, 5), В (-2,1), С (1, -2 ), и D (10, 2)

есть

d

AB

=

(

x - x

A )

2

+ y

- y

A )

2

=

(

-2 -1

2 + 1- 5

2

= 5,

B

( B

)

(

)

d

CD

=

(

x - x

2

+ y

- y

C )

2

= 32 + 42 = 5.

D

C )

( D

Аналогично:

d

BC

=

(

7 + 2

)

2

+ -2 -1

)

2

= 3 10,

(

d

DA

=

1-10

)

2

+ 5 - 2

)

2

= 3 10, то

естьВС = DA.

(

(

1°.

Координаты

точки М(х,у),

делящей

отрезок

M1M2

в

отношении

М1М

= l, (рис. 3.1) находятся по

формулам

ММ2

x =

x1 + lx2

; у =

у1 + l у2

(1)

1+ l

1+ l

Если точка М делит отрезок М1М 2

пополам, то l = 1 и

координаты равны

х1 + х2

y1 + y2

х =

; y =

.

(2)

2

2

Если l — число отрицательное, то точка М находится

на

продолжении

отрезкаM1M 2

и

деление

называется

Если,

следуя

по

контуру

треугольника

M

1

к M ик

M

3

, площадь

обходится

против часовой стрелки,

2

то

число S

положительное, в

противном

случае—

отрицательное. Поскольку площадь треугольника — величина

положительная,

то правая часть

формулы(3)

берется по

абсолютной величине.

х1 ( у2 - у3 ) + х2 (у3 - у1 ) + х3 ( у1 - у2 ) = 0,

(4)

которое

является

условием

,

чтотого

три

точки

M1 , M 2 и M 3

расположены на одной прямой.

3°. Площадь

многоугольника

с

вершинами

M1 (x1 , у1 ), М 2 (х2 , у2 ),...., М n (хn , уn ) определяется по формуле

S =

1

æ

x1

y1

+

x2

y2

+.... +

xn

yn

ö

.

(5)

ç

x2

y2

x3

y3

x1

y1

÷

2

è

ø

4°. Если

в

точкахM1 (x1 , у1 ), М 2 (х2 , у2 ),

М 3 (х3 , у3 )

помещены массы m1 , m2 , m3 соответственно, то координаты

центра тяжести этих масс находятся по формулам

x =

m1 x1 + m2 x2 + m3 x3

;

y =

m1 y1 + m2 y2 + m3 y3

(6)

c

m1 + m2 + m3

c

m1 + m2 + m3

Отсюда

координаты

центра

тяжести

площа

однородного треугольника определяются по формулам

x

=

x1 + x2 + x3

;

y

=

y1 + y2 + y3

(7)

c

3

c

3

из п

Координаты

центра

тяжести

системы, состоящей

материальных

точек M1 (x1 , у1 ), М 2 (х2 , у2 ),...., М n (хn , уn ),

соответственно с массамиm1 , m2 ,....mn ,

определяются по

формулам

-1+

3

×3

5

8 +

3

×3

2

х =

=

, у =

2

= 5

1 +

3

7

1+

3

2

2

2.2. Найти точку С, делящую отрезок между точками

А(-2) и В(4) на оси в отношении

l = -2.

Решение. Считаем,

что

точки A и B расположены на

оси х, тогда для отыскания точки С можно

воспользоваться

первой из формул (1)

х =

-1- 2 ×4

= 10

2.3. В

1- 2

треугольнике

с

А (-2, 0), В (6, 6), С (1, -4) определить

длину

медианы AD,

х =

6 +1

=

7

, у

D

=

6 - 4

=1.

D

2

2

2

5

Отсюда длина медианы AD =

(7 / 2 + 2)2 + 1(- 0)2 =

5.

2

Биссектриса АЕ делит

сторону ВС на

отрезки

AB

=

(6 + 2)2 + 62

=10;

AC

= (1 + 2 )2 + -(4 2 )= 5.

Отсюда l=2 и координаты точкиЕ

х =

6 + 2

=

8

; у

Е

=

6 - 2 × 4

= -

2

.

Е

1

+ 2

3

1 + 2

3

Длина биссектрисы АЕ

æ 8

ö

2

æ

2

ö

2

10

АЕ

=

ç

+ 2 ÷

+ ç

-

÷

=

2.

è 3

ø

è

3

ø

3

S =

1

é-2

(6 + 4)+ 6 -(4 - 0)+1 0( - 6)ù

= 25 кв.ед.

2

ë

û

Координаты центра тяжести находим по формулам (7)

х =

-2 + 6 +1

=

5

; y =

0 + 6 - 4

=

2

.

2.4.

Даны

3

3

3

3

три

последовательные

вершины

параллелограмма А (1,1), В (2, 2), С (3, -1).

Найти четвертую

вершину.

Решение.

Диагонали

параллелограмма

в

точк