Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2616

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.94 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2320 21 22 23 > Следующая >>>

2	2	2		(x ' )2				(y ' )2		(zx )2
4(x ' ) + 9	( y ' ) +16	(z ' ) = 9 или					+)	12	+				=)1.
				(3	2	2				(3	4	2
Таким	образом, данное					уравнение						определяет
эллипсоид (1) с центром в точке O '			(2, -2, -1)					и полуосями

a = 32, b =1, c = 34.

б) Уравнение не содержит произведений координат.

Преобразуем левую часть до полных квадратов

(

)

= (x +1)2 - 4 (y -1)2 + 4z2 - 4.

x2 + 2x +1- 4

y2 - 2 y +1

+ 4z 2 - 4

Полагая

x ' = x +1,

y ' = y -1,

z ' = z,

получим

уравнение

поверхности

системе

координатx ', y ', z ',

смещенной

относительно системы x, y, z

параллельным переносом начала

в точку O '(-1,1, 0)

(x ' )2

(x ' ) -

4 (y ' ) + 4

(z ' )

= 4

или

-( y '

) + z('

=) 1.

Поскольку в этом уравнении коэффициенты при (x ' )2

(z ' )2 положительные, а при ( y ' )2

— отрицательный, то данное

уравнение

определяет

однополостный

гиперболоид(3),

расположенный вдоль оси y ' .

в)

Преобразуя

левую

часть до полных квадратов,

приходим

уравнению(x - 5)2 -16( y + 2)2 - 4(z - 3)2 = 0 ,

из

которого после замены x ' = x -5,

y ' = y + 2,

z ' = z - 3

получим

уравнение

поверхности

системе

координатx ', y ', z ',

смещенной

относительно

системыx, y, z

параллельным

переносом

начала

координат

(5,-2,3)точку

(x ' )2 -16( y ' )2 - 4 (z ' )2 = 0.

Поскольку в этом уравнении свободный член

равен

нулю и

коэффициенты

при квадратах

координат

разных

знаков, то данное уравнение определяет конус второго порядка

(11) с осью вдоль оси x '

и вершиной в точке (5, -2,3).

191

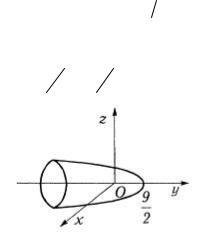
г) Данное уравнение содержит две координаты во второй степени одну в первой, следовательно, уравнение определяет эллиптический параболоид (5). Переписывая его в виде 5x2 + 3z2 = -2 (y - 92) , заключаем, что вершина

параболоида расположена в точке с координатами O '(0, 9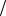2, 0)

и его полость обращена в сторону отрицательных значений y .

Если	обозначить x ' = x, y ' = y - 9 2, z ' = z,					то	получим
каноническое уравнение параболоида (рис. 4.16)
	(x ' )2	+	(zx	2)	= - y '.
	2	+	2		= - y '.
	5		3

Рис. 4.16

4.6. Геометрический смысл уравнений с тремя неизвестными в пространстве

1°. Рассмотрим		уравнение		с тремя неизвестными
F (x, y, z ) = 0.
Предположим, что уравнение может быть разрешено
относительно	z , то	есть z = f (x, y ).		Данное	уравнение	в
пространстве	представляет		поверхность		и	называетс
уравнением поверхности.
Если поверхность определена геометрически, .						е.
задано некоторое свойство, принадлежащее всем ее точкам и
не принадлежащее другим			точкам	пространства, то можно

192

составить			уравнение		этой	поверхности. Заданное
геометрическое				свойство,	выраженное		уравнением,
связывающим текущие координаты, и будет уравнением
поверхности.
	2°. Всякую линию в пространстве можно рассматривать
как	пересечение			двух	поверхностейF (x, y, z ) = 0			и
Ф (x, y, z ) = 0 . То есть,				линия в пространстве рассматривается
как	геометрическое			место	,точеккоординаты		которых
удовлетворяют системе этих уравнений.
	6.1.	Найти		геометрическое			место	,	то
равноудаленных			от	двух	данных	точекM (2,1, -1)		и
N (-3, 0, 3)

Решение. Пусть точка P(x, y, z) будет текущей точкой искомого геометрического места точек. Тогда, по формуле (11. Гл.2.2) данное условие примет вид

(x - 2)2 + (y -1)2 + (z +1)2 = (x + 3)2 + (y - 0)2 + (z -3)2 .

Упрощая, получим уравнение геометрического места точек

5x + y - 4z + 6 = 0 , Полученное уравнение изображает плоскость, перпендикулярную отрезку MN и пересекающую

его посередине.

6.2. Найти геометрическое место точек, удаленных на

расстояние 5 единиц от точки C (1,-2,1) .
Решение.	Пусть	точка M (x, y, z )		есть текущая	точка
поверхности.
Тогда,	по	условию		задачи	будем
(x -1)2 + (y + 2)2 + (z -1)2		= 25 .	Данное		уравнение

представляет сферическую поверхность с центром в точке C и радиусом R = 5 .

6.3. Каков геометрический смысл системы уравнений

193

	ìx2 + y2 + z2 = 25,
	í	z = 3.
Решение.	î	z = 3.
Решение.	Первое	уравнение	есть ,	сферавторое
представляет в	пространстве	плоскость. Подставляя		z = 3 в

первое уравнение, получим x2 + y2 =16 . То есть пересечение плоскости со сферой есть окружность, параллельная плоскости Oxy , с центром в точке C(0, 0,3) и радиусом равным 4.

6.4.Найти проекцию линии пересечения конуса

x2 + y2 - 3z2 = 0 (z ³ 0) и сферы (x -1)2 + y2 + z2 = 1

на координатную плоскость Oxy .

Решение.	Находим	уравнение	проектирующего
цилиндра.
Для этого	исключаем	из уравнений поверхностей

переменную z . Умножая второе уравнение на 3 и складывая с первым, получим

4x2 - 6x + 4 y2 = 0 .

Таким образом, проекция линии на плоскостьOxy

определяется

следующей

системой: x2 + y2 -

x = 0;

z = 0 .

Выделяя в первом уравнении полный квадрат, получим

ö2

ç x -

+ y

Следовательно,

проекция

линии

пересечения

поверхностей

на плоскостьOxy представляет

окружность с

центром в точке O1 (3

4 ; 0)

и радиусом, равным

6.5. Тело в пространстве задано системой неравенств. Определить вид поверхностей, ограничивающих это тело. Указать по каким линиям и в каких плоскостях пересекаются эти поверхности:

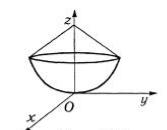
а) x2 + y2 < (z - 2)2 , x2 + y2 £ z ;

194


б)	x2 + y2 + z2 £ 25, x2 + y				2 £ 9;
в)	x2 + y2 - 9 ³ z2 ,		x2 + y2		£16.
Решение. )а		Уравнение		x2 + y2 = (z - 2)2				задает	в
пространстве	конус,	смещенный		вверх		по	осиOz на		2.
Неравенство	x2 + y2 £ (z - 2)2		показывает, что					поверхность
ограничивает тело внутри конуса.
Уравнение x2 + y2		= z задает в пространстве параболоид, а
неравенство x2 + y2 £ z			показывает,			что		поверхность
ограничивает	тело		внутри			параболоида. Объединяя

результаты, мы получим, что тело, ограниченное заданными поверхностями, имеет вид (рис. 4.17).

		Рис. 4.17
	Решая совместно уравнения поверхностей x2 + y2						= z и
x2 + y2	= (z - 2)2 , находим,		что z =1,		то есть	поверхности
пересекаются по окружности x2 + y2				=1 в плоскости z =1.
	б) Уравнение x2 + y2 + z2 = 25 задает сферу с центром в
начале	координат	и	радиусом		равным5. Неравенство
x2 + y2 + z2 £ 25 показывает,			что	ограничивает		тело	внутри
сферы.
Уравнение x2 + y2		= 9 задает цилиндрическую поверхность
с осью Oz и радиусом 3. Неравенство					x2 + y2 £ 9	показывает,

что ограничивает тело внутри цилиндра. Таким образом, тело, 195

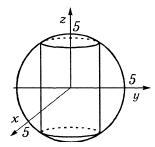
ограниченное заданными поверхностями, имеет					вид (рис.
4.18).
Очевидно, что		линиями	пересечения		поверхностей
будут окружности того же радиуса, что и направляющая
цилиндра.	Теперь	определим,	в	каких	плоскостях
пересекаются поверхности.
Для этого из системы уравнений исключимx и y .
Подставляя	x2 + y2 в	уравнение	сферы, получим		z2 =16 ,
z = ±4 . Следовательно,		поверхности		пересекаются		по
окружности в плоскостях z = ±4 .

			Рис. 4.18
в) Уравнение			x2 + y2 - z2 ³ 9	задет	в		пространстве
однополостный гиперболоид с осью вращенияOz и радиусом
окружности	в	плоскостиOxy		равным 3.	Неравенство
x2 + y2 - 9 ³ z 2		показывает, что		тело		находится		вне
поверхности.
Уравнение		x2 + y2 =16		задает			цилиндрическую
поверхность	радиуса 4 с осью Oz . Неравенство						x2 + y2 £16
показывает, что тело находится внутри цилиндра. Таким
образом,	тело		находится	между			однополостн
гиперболоидом и цилиндром (рис. 4.19).
Определим,		в	каких	плоскостях			пересекаются
поверхности.

196

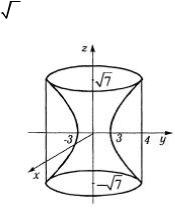
Исключая x, y из		системы		уравненийx2 + y2 - 9 = z2 ,
x2 + y2 = 16 ,	находим,	что	z2	= 7 .Отсюда	уравнения
плоскостей z =	7 .

Рис. 4.19

4.7. Параметрические уравнения пространственных кривых

1°. Уравнения вида

x = x (t ) , y = y (t ), z = z (t ),

(1)

где t — параметр, называются параметрическими уравнениями линии в пространстве.

Исключая из двух любых пар уравнений(1) параметр t, можно получить уравнение линии в виде двух уравнении с тремя переменными.


	2°. Цилиндрической			винтовой		линией	называется
линия,	которую	описывает		точкаM ,		движущаяся		по
поверхности кругового			цилиндра		радиусаR , обходя			его
кругом и одновременно поднимаясь вверх пропорционально
углу,	описываемому		ее	проекцией		на	горизонтальную
плоскость (рис. 4.20).
	Параметрические уравнения винтовой линии имеют вид
	x = R cos t,	y = R sin t, z = kt,			(k = Rtga > 0).			(2)

197

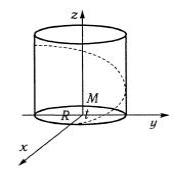
Если k > 0 , то	уравнения (2) называют	уравнениями
правой винтовой	линии, если же k < 0	эти уравнения

представляют левую винтовую линию.

Когда точка M совершит полный оборот, апликата z точки M увеличится на величину, называемую шагом или ходом винтовой линии, равным l = 2p Rtga .

Рис. 4.20

7.1. Определить линию, заданную уравнениями x = (t -1 2), y = 3(t +1) и z = -(t + 2) .

Решение. Исключая из второго и третьего уравнения


параметр	t , получим		y + 3z + 3 = 0			— уравнение		плоскости.
Находя из второго t и подставляя в первое уравнение, будем
иметь	9x = ( y - 2)2		—		параболический				цилиндр.
Следовательно, мы имеем линию пересечения плоскости с
параболическим цилиндром.
7.2.	Определить			линию,		заданную		уравнениями:
x = 3cos t ,	y = 4cos t , z = 5sin t
Решение.		Деля	первое		уравнение		на второе, получим
4x - 3y = 0 — уравнение плоскости.
Возводя в квадрат левые и правые части									каждого из
трех уравнений		и	складывая, получим				x2 + y2 + z2		= 25 —
уравнение сферы.
Следовательно,			мы		имеем		линию		пересечения
плоскости со сферой.

198

5.ЗАДАЧИ ДЛЯ ТИПОВОГО РАСЧЕТА

ИИТОГОВЫЙ КОНТРОЛЬ

		Задача №1.			p	,	q		,	r
Написать разложение вектора			x	по векторам	p	,	q		,	r	.
№ n/n	x	p		q						r
1.1.	(-2, 4, 7)	(0, 1, 2)		(1, 0, 1)	(-1, 2, 4)
1.2.	(6, 12, -1)	(1, 3, 0)		(2, -1, 1)	(0, -1, 2)
1.3.	(1, -4, 4)	(2, 1, -1)		(0, 3, 2)	(1, -1, 1)
1.4.	(-9, 5, 5)	(4, 1, 1)		(2, 0, -3)	(-1, 2, 1)
1.5.	(-5, -5, 5)	(-2, 0, 1)		(1, 3, -1)	(0, 4, 1)
1.6.	(13, 2, 7)	(5, 1, 0)		(2, -1, 3)	(1, 0, -1)
1.7.	(-19, -1, 7)	(0, 1, 1)		(-2, 0, 1)	(3, 1, 0)
1.8.	(3, -3, 4)	(I, 0, 2)		(0, 1, 1)	(2, -1, 4)
1.9.	(2, 2, -1)	(3, II, 0)		(-1, 2, 1)	(-1, 0, 2)
1.10.	(-1, 7, -4)	(-1, 2, 1)		(2, 0, 3)	(1, 1, -1)
1.11.	(6, 5, -14)	(1, 1, 4)		(0, -3, 2)	(2, 1, -1)
1.12.	(6, -1, 7)	(1, -2, 0)		(-1. 1, 3)		r		(1, 0, 4)
1.13.	(5, -15, 0)	(1, 0, 5)		(-1, 3, 2)	(0, -1, 1)
1.14.	(2, -1, 11)	(1, 1, 0)		(0, 1, -2)	(1, 0, 8)
1.15.	(11, 5, -3)	(1, 0, 2)		(-1, 0, 1)	(2, 5, -3)
1.16.	(8, 0, 5)	(2, 0, 1)		(1, 1, 0)	(4, 1, 2)
1.17.	(3, 1, 8)	(0, 1, 3)		(1, 2, -1)	(2, 0, -1)
1.18.	(8, 1, 12)	(1, 2, -1)		(3, 0, 2)	(-1, 1, 1)
1.19.	(-9, -8, -3)	(1, 4, 1)		(-3, 2, 1)	(1, -1, 2)
1.20.	(-5, 9, -13)	(0, 1, -2)		(3, -1, 1)	(4, 1, 0)
1.21.	(-15, 5, 6)	(0, 5, 1)		(3, 2, -1)	(-1, 1, 0)
1.22.	(8, 9, 4)	(1, 0, 1)		(0, -2, 1)	(1, 3, 0)
1.23.	(23, -14, -30)	(2, 1, 0)		(1, -1, 0)	(-3, 2, 5)
1.24.	(3, 1, 3)	(2, 1, 0)		(1, 0, 1)	(4, 2, 1)
1.25.	(-1, 7, 0)	(0, 3, 1)		(1, -1, 2)	(2, -1, 0)
1.26.	(11, -1, 4)	(1, -1, 2)		(3, 2, 0)	(-1, 1, 0)
1.27.	(-13, 2, 18)	(1, 1, 4)		(-3, 0, 2)	(1, 2, -1)
1.28.	(0, -8, 9)	(0, -2, 1)		(3, 1, -1)	(4, 0, 1)
1.29.	(8, -7, -13)	(0, 1, 5)		(3, -1, 2)	(-1, 0, 1)
1.30.	(2, 7, 5)	(1, 0, 1)		(1, -2, 0)	(0, 3, 1)

199


					Задача №2.
Определить коллинеарны ли векторы c1																															и c2 ,
построенные на векторах					и		.
				a		b
№ n/n		a											c1																													c2
					b
2.1.	(1, -2, 3)		(3, 0, -1)					2					+ 4																		3												-
									a																				b								b									a
2.2.	(1, 0, -1)		(-2, 3, 5)									+ 2																			3											-
								a									b																				a								b
2.3.	(-2, 4, 1)		(1, -2, 7)						5				+ 3																								2							-
										a														b														a									b
2.4.	(1, 2, -3)		(2, -1, -1)							4													+ 3								8											-
											a														b												a								b
2.5.	(3, 5, 4)		(5, 9, 7)					2						+																	3									- 2
												a				b																		a																		b
2.6.	(1, 4, -2)		(1, 1, -1)										+																					4																	+ 2
										a					b																				a																		b
2.7.	(1, -2, 5)		(3, -1, 0)					4															- 2																					- 2
									a																	b						b															a
2.8.	(3, 4, -1)		(2, -1, 1)						6				-3																															- 2
										a									b													b															a
2.9.	(2, -3, -2)		(1, 0, 5)					3					+ 9																															- 3
									a											b												a														b
2.10.	(-1, 4, 2)		(3, -2, 6)					2						-																				3							- 6
												a						b																	b																a
2.11.	(5, 0, -1)		(7, 2, 3)					2						-																				3							- 6
												a						b																	b																a
2.12.	(0, 3, -2)		(1, -2, 1)					5															- 2								3									+ 5
									a																			b						a															b
2.13.	(-2, 7, -1)		(-3, 5, 2)					2													+ 3										3									+ 2
											a														b									a																	b
2.14.	(3, 7, 0)		(1, -3, 4)					4															- 2																					- 2
									a																	b						b															a
2.15.	(-1, 2, -1)		(2, -7, 1)					6																			- 2																	- 3
										a																				b			b													a
2.16.	(7, 9, -2)		(5, 4, 3)					4						-																							4							-
												a						b																					b								a
2.17.	(5, 0, -2)		(6, 4, 3)					5					- 3																		6									-10
										a											b													b																			a
2.18.	(8, 3, -1)		(4, 1, 3)					2						-																	2											- 4
												a						b																		b																a
2.19.	(3, -1, 6)		(5, 7, 10)					4															- 2														- 2
									a																	b						a												b
2.20.	(1, -2, 4)		(7, 3, 5)					6					-3																									- 2
										a									b													b															a
2.21.	(3, 7, 0)		(4, 6, -1)					3															+ 2								5																	- 7
									a																		b							a																b
2.22.	(2, -1, 4)		(3, -7, -6)					2					- 3																		3									- 2
											a											b												a														b
2.23.	(5, -1, -2)		(6, 0, 7)					3					- 2																		4											- 6
									a														b													b																a
2.24.	(-9, 5, 3)		(7, 1, -2)					2						-																	3									+ 5
												a						b																a															b

200

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2320 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.93 Mб12605.pdf
#
15.11.20221.93 Mб12606.pdf
#
15.11.20221.93 Mб12609.pdf
#
15.11.20221.93 Mб22612.pdf
#
15.11.20221.94 Mб42614.pdf
#
15.11.20221.94 Mб12616.pdf
#
15.11.20221.94 Mб12617.pdf
#
15.11.20221.95 Mб02618.pdf
#
15.11.20221.95 Mб22619.pdf
#
15.11.20221.95 Mб12623.pdf
#
15.11.20221.95 Mб32624.pdf