
Практикум по линейной алгебре и аналитической геометрии. Пантелеев И.Н
.pdf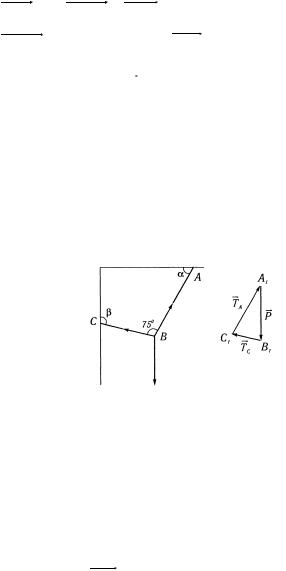
NM 1 |
= -(M 1M 2 |
+ M 2 N ) ; |
из |
|
треугольника ОМ2М1 |
находим |
|||||||||||||||||||||||||||
M |
|
M |
|
|
= rr |
- rr . Отсюда: NM |
|
= -(rr |
- rr |
+ |
1 |
( rr |
- rr |
))= |
|
||||||||||||||||||
1 |
2 |
|
1 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
2 |
|
3 |
2 |
|
|
||||
= rr |
|
1 |
(rr |
+ rr ); |
|
|
|
|
1 |
(rr |
|
1 |
(rr |
+ rr )). |
|
|
|
|
|
|
|
||||||||||||
- |
NM = |
- |
|
Подставляя |
найденные |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
2 |
|
2 |
|
|
3 |
|
|
|
3 |
|
1 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
значения |
|
векторов |
в |
выражение |
суммы |
|
векторов, получим |
||||||||||||||||||||||||||
r |
|
r |
|
|
1 |
|
r |
r |
|
1 |
|
r |
1 |
r |
|
r |
|
1 |
|
r r |
|
r |
|
|
|||||||||
R = r |
+ |
|
|
|
(r |
|
- r ) + |
|
|
(r - |
|
(r |
+ r )) = |
|
|
(r |
+ r |
+ r ). |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
3 |
2 |
|
3 |
|
1 |
|
|
2 |
2 |
|
3 |
|
3 |
|
1 |
2 |
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1.7. |
|
Электрический |
|
фонарь |
|
весом3кг |
подвешен к |
||||||||||||||||||||||
потолку на шнуре АВ и затем притянут к стенке веревкойВС
(рис. 2.14). |
|
|
|
Определить натяжение |
шнура |
и |
веревки, если |
известно, что угол a=60° , угол b=135°. |
|
|
|
Рис. 2.14
r r r
Решение. На точку В действует две силыTA , TC и P —
вес лампы. Поскольку система сил находится в равновесии, то равнодействующая этих сил равна нулю.
Построим треугольник сил. В выбранном масштабе r
строим вектор P (рис. 2.14). Через начало этого вектора
r
проведем линию действия силыTA , а через конец— линию
r
действия силы TC . Получим треугольник А1В1С1. Векторизуем
r  r
r
его стороны B1C1 = TC , C1 A1 = TA. Модули этих сил найдем по
теореме синусов.
Для этого определим углы при вершинах треугольника.
61
По условию задачи угол при вершине А1 равен 30°, при вершине B — 45°, значит, угол при вершине C1 равен 105°.
Учитывая, что sinl05°=sin75°, по теореме синусов имеем
TA |
= |
TC |
= |
P |
|
sin 45o |
sin 30o |
sin 75o |
|||
|
|
|
|
|
sin 45o |
|
|
sin 30o |
|
|
|
Откуда T |
A |
= 3 |
|
» 2,19 кг; |
T |
= 3 |
|
»1,55 кг. |
|
|
|
|
|||||||
|
|
sin 75o |
C |
|
sin 75o |
|
|
||
|
|
|
|
|
|
|
|||
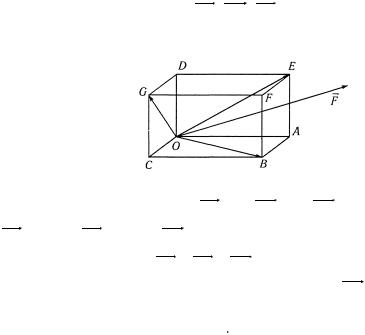
1.8. К вершине О прямоугольного параллелепипеда |
|
||||||||
ABCOGDEF (рис. 2.15) |
приложены |
три |
силы, |
||||||
изображаемые |
|
векторами OE, OG, OB , |
найти |
величину |
и |
||||
|
|
|
|
r |
|
|
|
|
|
направление равнодействующей F . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
Рис.2.15 |
r |
r |
|
||
|
|
|
|
|
|
|
|
r |
|
|
||
Решение. Обозначим OA = a, OC = b, OD = c , тогда |
||||||||||||
r |
r |
|
r |
r |
|
|
r |
r |
|
|
|
|
OB = a |
+ b, OE = a |
+ c, OD = b + c. |
|
|
|
|
||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
Поскольку F = OB + OE + OG , то |
r |
|
|
|||||||||
|
r |
r |
r |
r |
r |
r |
r |
r |
r |
|
|
|
|
F = a |
+ b + a |
+ c + b + c |
= 2(a |
+ b + c) = 2OF, |
|
||||||
т. е. |
равнодействующая |
|
r |
|
изображается |
удвоенной |
||||||
|
F |
|
||||||||||
диагональю параллелепипеда OF .
2.2. Разложение вектора по координатным осям
1°. Всякий вектор в пространстве можно представить как сумму трех векторов, один из которых расположен на оси Ох, второй на оси Оу и третий — на оси Oz
62

r |
r |
r |
r |
(1) |
a |
= axi + ay j + az k |
|||
r r r
где i , j, k — единичные векторы координатных осей.
|
|
r |
равен |
|
||
Модуль вектора a |
|
|||||
r |
= |
|
2 |
2 |
2 |
(2) |
a |
ax |
+ ay |
+ az . |
|||
r
Если через a, b, g обозначить углы, которые вектор a
составляет с положительными направлениями координатных осей, то формулы
cosa = |
ax |
|
, cos b = |
ay |
|
, cosg = |
az |
|
(3) |
|||
|
r |
|
|
r |
|
|
r |
|
||||
|
|
a |
|
|
|
a |
|
|
|
a |
|
|
r
дают выражения направляющих косинусов вектораa через его проекции.
Между направляющими косинусами существует зависимость
|
|
cos2 a + cos2 b + cos2 g = 1. |
|
(4) |
||
2°. Действия над векторами. |
|
|
||||
1. |
Сумма векторов |
r |
r |
|
||
|
r |
r |
r |
(5) |
||
|
a ± b = (ax |
± bx )i + (ay |
± by ) j + (az ± bz )k . |
|||
2. |
Умножение на скаляр |
r |
|
|
||
|
r |
r |
r |
|
|
|
|
la |
= laxi + lay j + laz k . |
|
(6) |
||
3. |
а) Если A(x1, y1, z1) и B(x2, y2, z2) |
— координаты |
||||
начала и конца вектора, то проекции вектора |
|
|
||||
|
ax = x2 – x1, ay = y2 – y1 , az = z2 – z1 . |
|
(7) |
|||
б) Модуль |
|
|
|
|
||
r |
|
|
(x2 - x1 ) |
2 |
+ ( y2 |
- y1 ) |
2 |
+ (z2 - z1) |
2 |
|
|
|
||||||
a = |
|
|
|
|
|
|
|
|||||||||||
в) Направляющие косинусы |
|
|
|
|
|
|
|
|||||||||||
|
x |
2 |
- x |
|
|
|
y |
- y |
|
|
z |
2 |
- z |
|||||
cosa = |
|
r |
1 |
; cos b = |
|
2 |
r |
|
1 |
; cosg = |
|
|
r |
1 |
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
(8)
(9)
г) Если некоторая осьl составляет с координатными
r
осями углы a, b, g , то проекция произвольного вектора a на эту ось определяется равенством
63

r |
cosg . |
(10) |
Прl a = ax cosa + ay cos b + az |
||
3°. Задачи на точку. |
|
|
1. Расстояние между точками |
|
|
M1(x1, y1, z1) и M2(x2, y2, z2) определяется по формуле |
||
|
|
d= |
(x - x )2 + ( y |
2 |
- y )2 |
+ (z |
2 |
- z )2 . |
(11) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
Если начало отрезка совпадает с началом координат, то |
|||||||||||||||||||||||||||||||||
формула (11) примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
d= |
x2 + y2 + z 2 . |
|
|
|
|
|
|
|
|
|
|
(12) |
|||||||||||||
2. Деление |
|
отрезка М1М2 |
|
в |
|
заданном отношении l. |
|||||||||||||||||||||||||||
Координаты |
точки M (x,y,z) |
делящей |
отрезок М1М2 |
|
в |
||||||||||||||||||||||||||||
отношении |
M1M |
|
= l находятся по формулам |
|
|
||||||||||||||||||||||||||||
MM 2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rr1 + l rr2 |
|
||||
x = |
x1 + lx2 |
; |
|
y = |
y1 + ly2 |
|
|
; |
z = |
z1 + lz2 |
|
или rr = |
. |
||||||||||||||||||||
|
|
1 + l |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 + l |
|
|
|
|
|
|
|
|
|
|
1 + l |
|
|
|
2 |
|
|
|||||||||||||||
Если точка М делит отрезокМ1М2 |
пополам, то l = 1 и |
||||||||||||||||||||||||||||||||
формулы (13) примут вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x = |
x1 + x2 |
, |
|
y = |
y1 + y2 |
, |
z = |
z1 + z2 |
. |
|
(15) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3. Координаты центра тяжести системы п материальных |
|||||||||||||||||||||||||||||||||
точек массы mi, |
|
расположенных |
в |
пространстве, находят по |
|||||||||||||||||||||||||||||
формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
= |
åin=1 mi xi |
|
, y |
|
= |
åin=1 mi yi |
, |
z |
|
= |
åin=1 mi zi |
. |
(16) |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
c |
|
|
åin=1 mi |
|
|
c |
|
|
åin=1 mi |
|
|
|
|
c |
|
|
|
åin=1 mi |
|
|
||||||||||||
2.1. Заданы начало A(3,2,-1) и конец B(1,5,2) вектора
AB .
Найти разложение вектора AB по координатным осям, его модуль и направляющие косинусы.
Решение. Найдем по формулам (7) проекции вектора на координатные оси
(AB)x =1-3=-2; (AB)y =5-2=3; (AB)z=2+1=3.
r r r
Отсюда вектор равен AB = - 2i + 3 j + 3k , а его модуль
64
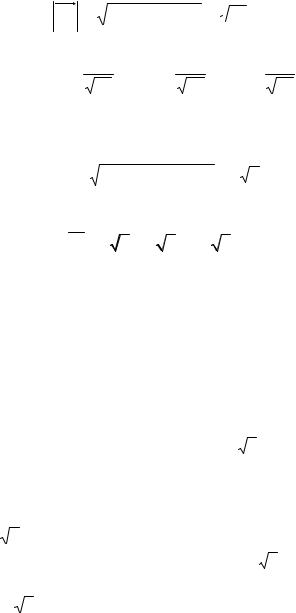
AB = (-2)2 + 32 + 32 =  22 .
22 .
|
По формулам (9) направляющие косинусы |
|
||||||||||||||||||||||
|
|
cosa = - |
|
2 |
|
, cos b = |
3 |
|
, cosg = |
3 . |
|
|||||||||||||
|
2.2. |
Найти |
|
22 |
|
|
|
|
|
|
22 |
|
|
|
|
|
22 |
|
||||||
r |
|
|
единичный |
|
|
|
|
вектор |
для |
вектора |
||||||||||||||
r r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
= 3i - 5 j - 4k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Находим модуль вектора | a | по формуле (2) |
|
||||||||||||||||||||||
|
|
|
|
r |
\ = |
3 |
2 |
+ (-5) |
2 |
+ (-4) |
2 |
= 5 2 . |
|
|
||||||||||
|
|
|
\ a |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
r |
0 |
находим по формуле |
|
|
||||||||||||||
Единичный вектор a |
|
|
|
|||||||||||||||||||||
|
|
r |
|
|
|
r |
|
|
|
|
3 r |
|
5 |
|
r |
|
|
4 |
|
r |
|
|
||
|
|
0 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
|
= |
|
r |
|
= |
|
|
|
i - |
|
|
|
|
j - |
|
|
|
|
k . |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
5 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
a |
|
5 |
|
|
|
|
|
|
|
|
|
|||||||
2.3.Найти сумму векторов
|
|
r |
r |
r |
r r |
r r |
r |
r |
r |
r |
r |
|
|
|
a = 3i + 2 j + 5k , b = 4i - j + 3k , c = -i + 2 j + 2k . |
||||||||||
r |
r |
Решение. По формуле (5) находим |
r |
r |
r |
r |
||||||
r |
|
r |
|
r |
|
|
||||||
a |
+ b + c = (3 + 4 -1)i + (2 -1 + 2) j + (5 + 3 + 2)k = 6i + 3 j +10k . |
|||||||||||
|
|
|
|
|
|
|
r |
(2;4;-1), |
r |
|
|
|
|
|
2.4. Найти разность векторов a |
b (4;-3;5). |
|||||||||
|
|
Решение. По формуле (5) находим |
r |
r |
r |
|
||||||
|
|
r |
r |
r |
|
r |
|
r |
|
|||
|
|
a - b = (2 - 4)i + (4 + 3) j + (-1 -5)k = -2i + 7 j -6k . |
||||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
2.5. Определить координаты вектора b , если известно, |
||||||||||
|
|
|
|
|
|
|
r |
r |
r |
r |
и его |
|
что | b | = 5 |
, он коллинеарен вектору a = |
7i - 5 j + 2k |
||||||||||
направление совпадает с направлением вектора |
r |
|
|
|||||||||
a . |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
Решение. Обозначим координаты вектора b через х, у z, |
|||||||||||
т. е. |
r |
|
Поскольку |
векторы |
|
коллинеарные, то |
||||||
b ={x,y,z}. |
|
|||||||||||
r |
r |
|
r |
r |
r |
|
|
|
|
|
|
|
b = la |
= 7li - 5lj + 2lk . |
|
r |
r |
r |
r |
r |
r |
||||
|
|
Из |
равенства |
|
|
|||||||
|
|
векторовxi + yj + zk = |
7li - 5lj + 2lk |
|||||||||
следует равенство их координат: |
|
|
r |
|
|
|
||||||
|
|
x = |
7l, y = -5l, z = 2l . |
Так |
как |
= 5 |
, |
то по |
||||
|
|
| b | |
||||||||||
формуле (2) имеем
65
7l2 + (-5l)2 + (2l)2 |
= 5 , откуда l = ± |
5 |
. Поскольку |
||
|
|||||
r |
r |
6 |
|
||
совпадают, то следует взять l >0, |
|||||
напрaвления векторов a |
и b |
||||
т. е. l = 5 . 6
Таким образом, координаты искомого вектора будут: x = 5 , y = - 25 , z = 5 .
|
6 |
6 |
3 |
2.6. На |
векторах |
r |
r |
a |
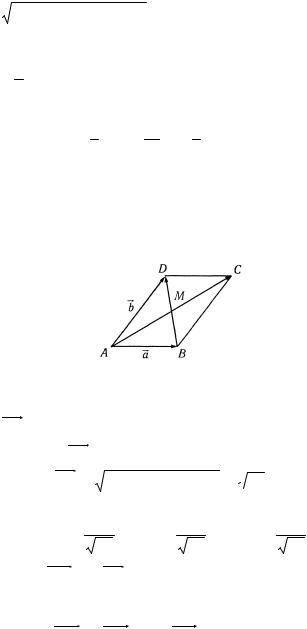
(3;1;4) и b (-2;7;1) построен |
параллелограмм.
Найти величину и направления его диагоналей.
r
r
Решение. Из точки А отложим векторы a и b и построим параллелограмм ABCD (рис. 2.16).
Рис. 2.16
Векторизуем стороны и диагонали параллелограмма. Из треугольника ABC диагональ
r |
r |
r |
r |
r |
r r r |
BD = b - a |
= (-2 - 3)i + (7 - 4) j + (1 - 4)k = -5i + 6 j - 3k . |
||||
Модуль вектора BD равен
\ BD \= (-5)2 + 62 + (-3)2 =  70 .
70 .
Направляющие косинусы определим по формулам (3)
cosa = - 5 |
, cos b = |
6 , cosg = - |
3 . |
||||
|
70 |
70 |
|
r |
70 |
||
|
1 |
|
r |
r |
|
|
|
Вектор BM = |
|
|
BD = - 2,5i |
+ 3 j -1,5 k . |
|
||
2 |
|
|
|||||
|
|
|
|
|
|
|
|
Из треугольника ABM находим вектор |
r |
||||||
|
|
|
r |
|
1 r r |
||
AM : |
|
|
AM = a + BM = |
|
i + 4 j + 2,5k . |
||
|
|
2 |
|||||
|
|
|
|
|
|
|
|
66
Отсюда |
вектор |
|
|
|
|
r |
r |
r |
||
AC = 2 AM равен AC = i + 8 j + 5k . |
||||||||||
Длина диагонали АС равна \ AC \= |
12 + 82 + 52 |
= |
90 , а |
ее |
||||||
направление определяется направляющими косинусами |
|
|||||||||
cosa |
1 |
= - |
1 |
, cos b = |
|
8 |
, cosg = - |
5 . |
|
|
|
3 |
10 |
1 |
3 |
10 |
3 |
10 |
|
||
|
|
|
|
|||||||
2.7. Даны точки А (1,2,-1) и В (4,-3,2). Найти проекции
вектора AB на ось, составляющую с координатными осями равные острые углы.
Решение. По условию задачи направляющие косинусы равны друг другу и из условия cos2a + cos2b + cos2g = 1
следует, |
что cos a = cos b = cos g = |
|
1 |
|
. Вектор |
AB |
имеет |
||||
|
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
проекции AB (3, - 5 , 3). Отсюда по формуле (10) находим, что |
|||||||||||
искомая проекция на ось равна Пр AB = |
3 - |
5 |
+ |
3 = |
3 . |
||||||
|
|
|
l |
|
|
3 |
3 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
||||
2.8. Найти величину и направляющие равнодействующей |
|||||||||||
r |
r |
r |
r |
|
|
|
|
|
|
|
|
R трех сил F1 {14,5,4}, F2 {-6,2,7}, F3 |
{4,2,9} . |
|
|
|
|
||||||
Решение. Находим |
проекции |
равнодействующей как |
|||||||||
сумму |
проекций |
|
r |
r |
r |
|
r |
Величина |
|||
компонентовR =12i |
+ 9 j + 20k . |
||||||||||
равнодействующей |
r |
144 + 81 + 400 = 25 . |
Направление |
||||||||
R = |
|||||||||||
равнодействующей определяется направляющими косинусами cosa = 12 , cos b = 9 , cosg = 4 .
25 |
25 |
5 |
2.9. Даны точки |
A(1,2,3) и |
B(-1,4,2). Найти длину |
отрезка АВ и координаты точки С, делящей отрезок в
отношении l = 1 .
3
Решение. Применяя формулу (11), находим длину
отрезка dAB =  (-1 -1)2 + (4 - 2)2 + (2 - 3)2 = 3 .
(-1 -1)2 + (4 - 2)2 + (2 - 3)2 = 3 .
Координаты точки С находим по формулам (13)
67
|
|
|
1 + |
1 |
(-1) |
|
|
1 |
|
|
|
|
|
|
2 + |
1 |
× 4 |
|
5 |
|
|
|
|
3 + |
1 |
× 2 |
|
|
|
11 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
x = |
3 |
|
|
|
|
= |
|
|
y = |
|
|
|
|
3 |
|
|
|
= |
|
z |
= |
|
3 |
|
|
|
= |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||
1 + |
1 |
|
|
2 |
|
|
|
1 + |
1 |
|
|
2 |
|
1 + |
1 |
|
|
|
4 |
|
|||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.10. Отрезок |
|
|
АВ |
|
делится |
|
|
точкой |
|
С в |
|
отношении, |
|||||||||||||||||||||||||||||||||||||||||
равном 2. По данным точкам А (3,4,-1) и С (2,-3,1) найти точку |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Используя |
|
|
|
|
формулы |
|
деления |
|
|
|
|
отрезка |
в |
||||||||||||||||||||||||||||||||||||||||
данном отношении (13), выразим координаты точки В |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
x = |
(1 + l)x - x1 |
, y |
2 |
= |
|
(1 + l) y - y1 |
, z |
2 |
= |
(1 + l)z - z1 |
. |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Подставляя данные условия, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
x = |
3 × 2 - 3 |
= 1,5 , |
y |
|
= |
3 × (-3) - 4 |
= -6,5 , |
z |
|
= |
3 ×1 +1 |
|
= 2 . |
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.3. Скалярное произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1°. Скалярным произведением двух векторовa |
|
и b |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
называется скаляр (число), |
|
равное |
произведению |
|
|
|
модулей |
|
|||||||||||||||||||||||||||||||||||||||||||||
перемножаемых векторов на косинус угла между ними |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
r |
|
× |
|
r |
cosj . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a ×b = |
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2°. Свойства. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. Переместительность |
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
×b = b × a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2. Распределительность |
|
r |
|
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
|
r |
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
( a |
+ b ) c |
= ( a |
×c ) + ( b × c ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3. Скалярный множитель можно выносить за знак |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
скалярного произведения |
r |
|
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(l a× b ) = l( a×b ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4. |
|
Скалярный |
|
|
|
квадрат |
|
|
|
|
вектора |
|
равен |
квадрату |
его |
||||||||||||||||||||||||||||||||||||||
модуля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a × a |
|
= a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5. |
|
|
Скалярное |
|
|
|
|
|
произведение |
|
единичных |
|
|
|
|
векторов |
|||||||||||||||||||||||||||||||||||||
определяется формулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
68

|
r r |
= |
r r |
|
r r |
|
r r |
r r |
r r |
|
(6) |
||||||||||||
|
i × i |
|
j × j |
= k × k = 1, i × j |
= j × k = k × i |
= 0 . |
|||||||||||||||||
|
3°. |
Выражение |
|
скалярного |
|
|
|
произведения |
через |
||||||||||||||
проекции перемножаемых векторов. Скалярное произведение |
|||||||||||||||||||||||
двух |
векторов |
|
|
равно |
|
сумме |
произведений |
одноименных |
|||||||||||||||
проекций перемножаемых векторов |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||
|
|
|
|
|
a ×b = axbx + ayby + azbz . |
|
|
|
|
|
|||||||||||||
|
Угол между двумя векторами |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
r |
r |
|
r |
r |
|
|
|
axbx + ayby + azbz |
|
|
|
|
||||||||||
|
|
a |
×b |
|
|
|
|
2 . |
|
(8) |
|||||||||||||
|
cos(a ,b ) = |
|
r |
r |
= |
|
2 |
|
|
2 |
2 |
|
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|
a b |
|
|
ax |
+ ay |
+ az |
|
bx |
+ by |
+ bz |
|
|
|||||||
|
Условие перпендикулярности двух векторов |
|
|
||||||||||||||||||||
|
|
|
|
axbx + ayby + azbz = 0. |
|
|
|
|
|
|
|
(9) |
|||||||||||
|
Косинус |
|
|
|
угла |
|
между |
|
|
двумя |
направлениями |
||||||||||||
пространстве |
|
равен |
сумме |
произведений |
одноименных |
||||||||||||||||||
направляющих косинусов этих направлений |
|
|
|
|
|
|
|||||||||||||||||
|
cosj = cosa1 cosa2 + cos b1 cos b2 + cosg1 cosg2 . |
(10) |
|||||||||||||||||||||
|
Условие перпендикулярности двух направлений |
|
|
||||||||||||||||||||
|
cosa |
|
cosa |
|
+ cos b cos b |
|
+ cosg |
|
cosg |
|
= 0. |
|
(11) |
||||||||||
|
|
1 |
|
|
2 |
|
|
1 |
r |
|
2 |
|
|
1 |
|
|
2 |
|
|
произведению |
|||
|
4°. Работа A силы |
F равна скалярному |
|||||||||||||||||||||
вектора силы на вектор перемещения |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
A = |
r |
r |
|
|
r |
|
r |
|
|
|
|
|
|
|
(12) |
|||
|
|
|
|
|
F |
S |
cos(F, S ) . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r |
3.1. Найти скалярное произведение векторов 2 a |
-3 b |
и |
||||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c +4 d . |
|
|
|
|
|
|
|
|
|
r |
|
r |
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Решение. Находим (2 a -3 b ) ( c +4 d ) = |
r |
|
|
|
||||||||||||||||||
|
|
|
|
= 2 |
r |
r |
r |
r |
|
r r |
|
|
r |
|
|
|
|
|
|||||
|
|
|
|
a |
× c + |
8a |
× d - 3b × c |
-12b × d . |
|
|
|
||||||||||||
|
3.2. Дан ромб ABCD (рис. 17). Доказать, что |
его |
|||||||||||||||||||||
диагонали пересекаются под прямым углом. |
|
|
|
|
|
|
|||||||||||||||||
|
Решение. Векторизуем стороны и диагонали ромба, |
||||||||||||||||||||||
как |
|
показано |
|
|
|
на |
. 2.17. рис Тогда |
имеем |
|||||||||||||||
AC = AB + BC, |
DB = DA + AB. |
|
|
Поскольку DA = -BC , |
то |
||||||||||||||||||
69

DB = AB - BC . |
Составим |
скалярное |
произведение |
||||
векторов AC и DB : |
|
|
|
|
|
|
|
AC × DB =( AB + BC) ( AB - BC) = ( AB)2 - (BC)2 = 0 |
,так как в |
||||||
|
|
|
|
|
|
|
|
ромбе все |
стороны |
равны |
ABи |
= |
BC |
. |
Поскольку |
|
|
|
|
|
|
|
|
скалярное произведение векторов—диагоналей AC и DB равно нулю, то эти векторы взаимно-перпендикулярны, что и требовалось доказать.
Рис. 2.17
r |
3.3. |
|
Найти |
r |
косинус |
угла |
|
между |
векторами |
|||||||||
r r |
r |
r |
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|||
a |
= 2i - 3 j + 5k , b = i - j + 3k . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Решение. Используя формулу (8), имеем |
|
|
|
||||||||||||||
|
r |
r |
r |
r |
|
|
axbx + ayby + azbz |
|
|
|
|
|
|
|||||
|
a ×b |
|
|
|
|
|
= |
|
|
|||||||||
|
cos(a ,b ) = r |
r |
= |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
|||||||
|
|
|
|
a b |
|
ax |
+ ay + az |
bx |
+ by |
+ bz |
|
|
|
|||||
|
= |
|
2 ×1 + (-3)(-1) + 5 × 3 |
|
= |
20 . |
|
|
|
|
||||||||
|
22 + (-3)2 + 52 12 + (-1)2 + 32 |
|
418 |
|
|
|
|
|||||||||||
|
3.4. |
|
Определить |
|
углы |
|
треугольника ABC |
с |
||||||||||
вершинами A(1,1,1); B(2-1,3) и С(0,0,5). |
|
|
|
|
|
|
||||||||||||
|
Решение. Найдем координаты векторов AB и |
AC : |
||||||||||||||||
AB (1,-2,2), |
AC (-1,-1,4). |
Угол |
между |
ними |
находим |
по |
||||||||||||
формуле (8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
cosA= |
|
|
1(-1) + (-2)(-1) + 2 × 4 |
|
|
= |
|
2 |
, |
A = 45o . |
|
||||||
|
|
12 + (-2)2 + 22 |
(-1)2 + (-1)2 + 42 |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
70
