2760.Практикум по теории механизмов и механике систем машин
..pdf


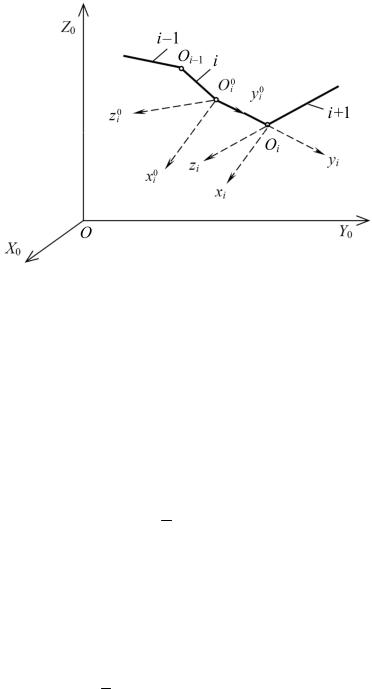
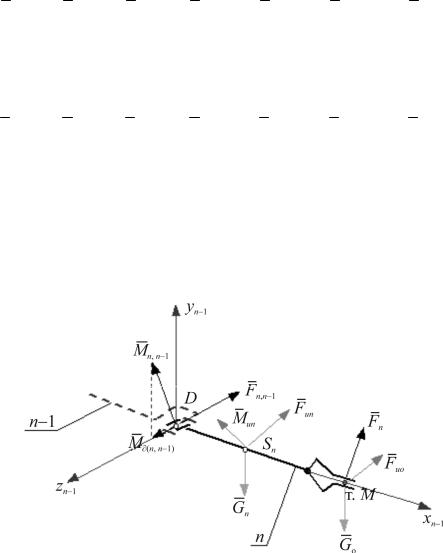
Рис. 8.9. Связанные системы координат с началом в центре кинематической пары (Oi xi yi zi ) и в центре
|
|
инерции |
(O0 x0 y0 z |
0 ) |
|
|
||||
|
|
|
|
|
i |
i i |
|
i |
|
|
Jxi yi |
= J yi xi |
= xi yidmi , |
|
|||||||
Jxi zi |
= Jxi zi |
= xi zidmi |
, |
(8.10) |
||||||
J |
yi zi |
= J |
zi yi |
= |
|
i i |
|
|
|
|
|
i |
|
||||||||
|
|
|
y z |
dm |
|
|
||||
и также являются известными константами.
Определим вектор скорости Viц центра инерции звена i через проекции на оси связанной с ним системы координат:
|
|
|
|
ц = (Vixц,Viyц,Vizц )T , |
(8.11) |
|
|
Vi |
|||
или через проекции на оси неподвижной системы осей: |
|
||||
|
|
V0iц = (V0ixц,V0iyц,V0izц )T . |
(8.12) |
||
|
|
ц введем вектор угловой скорости звена |
|
||
По аналогии с Vi |
|
||||
|
|
ϖi = (ϖix ,ϖviy ,ϖiz )T |
(8.13) |
||
и запишем равенство (8.6) в развернутой форме для случая, когда звенья манипулятора обладают симметрией относительно главных осей инерции.
Для этого подставим выражения θ0 , |
|
|
, ϖ |
|
из (8.7), (8.11), (8.13) в (8.6) |
V |
i |
||||
Oi |
|
iц |
|
||
и получим следующее:
225