2760.Практикум по теории механизмов и механике систем машин
..pdf
При совершении двух конечных поворотов тела вокруг осей, определяемых ортами e1 , e2 , результирующий поворот находится по формуле
где |
|
= |
|
tg |
ϕ |
|
; |
|
θ |
||||||||
e |
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
θ = |
|
θ1 + θ2 |
− |
|
θ1 × θ2 |
, |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1− θ1θ2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
= |
e1tg ϕ1 |
|
; |
|
|
|
|
= |
e2tg ϕ2 |
|
; |
|
|
– орт результирующего |
|||||||||||
|
θ |
|
|
θ |
||||||||||||||||||||||||
|
1 |
|
|
2 |
e |
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
вектора.
Последняя формула показывает, что результирующий поворот двух конечных поворотов твердого тела вокруг неподвижных осей зависит от порядка выполнения этих поворотов.
8.5.2. Решение задач кинематики методом преобразования координат
Первая и основная задача кинематики – определение функции положения. В прямой задаче о положениях необходимо определить положение выходного звена как функцию перемещений в приводах, в обратной – перемещения в приводах как функцию заданного положения выходного звена.
При решении прямой задачи о положении схвата манипулятора обычно используют метод преобразования координат. Из множества методов преобразования координат [1, 2], которые отличаются друг от друга правилами выбора осей локальных систем координат, для манипуляторов обычно используется метод Дж. Денавита и Р. Хартенберга.
Опишем два вида матриц:
–матрицы М, определяющие отношение между системами координат соседних звеньев;
–матрицы Т, определяющие положение и ориентацию каждого звена механизма в неподвижной или базовой системе координат.
Воспользуемся однородными координатами трехмерного проективного пространства РR3, в которых движение эвклидова пространства R3 можно представить линейным преобразованием
|
|
|
|
|
|
|
|
|
|
= Mij |
|
|
|
|
||
|
|
|
|
|
|
|
|
ri |
rj , |
|||||||
где |
|
и |
|
|
– радиус-вектор соответственно в старой и новой системах коор- |
|||||||||||
ri |
rj |
|||||||||||||||
динат; Мij |
– матрица 4×4 вида |
|
Uij |
b |
|
; Uij – матрица поворота; |
|
– вектор |
||||||||
|
|
|||||||||||||||
|
|
b |
||||||||||||||
|
|
|
|
|
|
|
000 |
1 |
|
|
|
|
|
|
||
переноса.
211
Это преобразование эквивалентно преобразованию в эвклидовом про-
странстве |
|
= U |
|
|
|
|
+ |
|
, где |
|
|
, |
|
|
|
R3 |
, т.е. преобразованию, которое включа- |
|
|
|
|
|
b |
|
|
||||||||||
r |
ij |
r |
j |
r |
r |
j |
|||||||||||
|
i |
|
|
|
|
|
i |
|
|
||||||||
ет поворот, определяемый матрицей Uij размерностью 3×3, и параллельный перенос, задаваемый вектором b размерностью 3. В однородном пространстве положение точки будут определять не три x, y и z, а четыре величины x', y', z' и t', которые удовлетворяют следующим соотношениям:
x = x'/t', y = y'/t', z = z'/t'.
Обычно принимают t' = 1. У матрицы поворота Uij элементами uij являются направляющие косинусы углов между новой осью i и старой осью j. Вектор b = (x, y, z) является трехмерным и определяет положение начала
новой системы координат i в старой системе j.
Выбор расположения и ориентации локальных систем координат должен соответствовать типу решаемой задачи (прямая или обратная).
При использовании метода Денавита–Хартенберга оси координат располагаются по следующим правилам:
1.Для звена i ось zi направляется по оси кинематической пары, образуемой им со звеном (i + 1). Начало координат размещают в геометрическом центре этой пары.
2.Ось xi направляется по общему перпендикуляру к осям zi–1 и zi с направлением от zi–1 к zi. Если оси zi–1 и zi совпадают, то xi перпендикулярна им и направлена произвольно. Если они пересекаются в центре кинематиче-
ской пары, то начало координат располагается в точке пересечения, а ось xi направляется по правилу векторного произведения xi = zi × zi−1 (кратчайший
поворот оси zi до совмещения с zi–1 при наблюдении с конца xi должен происходить против часовой стрелки).
3. Ось yi направляется так, чтобы система координат была правой.
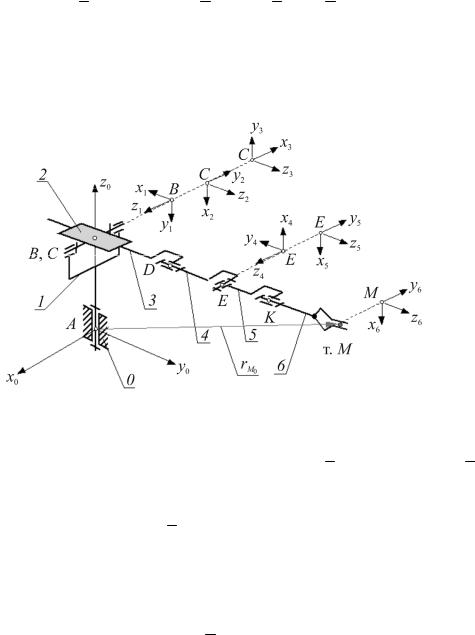
В прямой задаче необходимо определить положение схвата манипулятора и связанной с ним системы координат xnynzn по отношению к неподвижной или (базовой) системе координат x0y0z0. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена i–1. Согласно принятому методу каждый переход включает в себя последовательность четырех движений: двух поворотов и двух параллельных переносов, осуществляемых в указанной последовательности (рис. 8.5):
–поворот i-й системы вокруг оси xi на угол θi до параллельности осей zi
иzi–1 (положительное направление поворота при наблюдении с конца вектора xi против часовой стрелки);
212
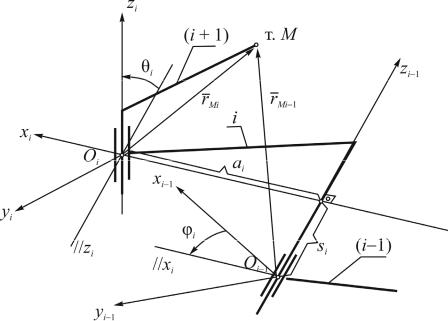
Рис. 8.5. Последовательность расчета прямой задачи кинематики
–перенос вдоль оси xi на величину ai до совмещения начала системы координат Oi с точкой пересечения осей xi и zi–1 (отсчитывается по оси xi от точки пересечения оси xi и оси zi–1);
–перенос вдоль оси zi–1 на величину si, после которого начало системы координат Oi оказывается в начале координат Oi–1 системы (i–1) (отсчитывается по оси zi–1 от ее начала координат Oi–1 до точки ее пересечения с осью xi);
–поворот вокруг оси zi–1 на угол φi до тех пор, пока ось xi не станет параллельной оси xi–1 (положительное направление поворота при наблюдении
сконца вектора zi–1 против часовой стрелки).
Необходимо отметить, что знак угла поворота не имеет значения, так как в матрицах перехода используются направляющие косинусы (четные функции). Целесообразно рассматривать угол, обеспечивающий кратчайший поворот оси старой системы i до совмещения (параллельности) с соответствующей осью новой (i–1). Перемещения начала координат определяются как координаты начала Oi старой системы в новой.
В манипуляторах обычно используются одноподвижные вращательные или поступательные кинематические пары. Оба относительных движения, как вращательное, так и поступательное, реализуются в цилиндрических парах. Поэтому при общем представлении механизма (см. рис. 8.5) используются цилиндрические пары. Матрицы перехода из системы i в систему i–1 можно записать так:
Mi = Miθ Mia Mis Miϕ ,
где Miθ – матрица поворота вокруг оси xi на угол θi,
213

|
1 |
0 |
0 |
0 |
|
|
|
||||
Miθ = |
0 |
cosθi |
− sin θi |
0 |
; |
|
0 |
sin θi |
cosθi |
0 |
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
Mia – матрица переноса вдоль оси xi на ai,
|
1 |
0 |
0 |
ai |
|
|
|
||||
Mia = |
0 |
1 |
0 |
0 |
; |
|
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
Mis – матрица переноса вдоль оси zi–1 на si,
|
1 |
0 |
0 |
0 |
|
|
|
|
|||||
Mis = |
0 |
1 |
0 |
0 |
|
; |
|
0 |
0 |
1 |
si |
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
Miϕ – матрица поворота вокруг оси zi–1 на угол φi.
|
cosϕi |
− sin ϕi |
0 |
0 |
|
|
|
|
|||||
Miϕ = |
sin ϕi |
cosϕi |
0 |
0 |
|
. |
|
0 |
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
В этих матрицах переменные si и φi соответствуют относительным перемещениям звеньев в кинематических парах и являются обобщенными координатами манипулятора, определяющими конфигурацию механизма в рассматриваемом положении. Переменные ai и θi определяются конструктивным исполнением звеньев манипулятора, в процессе движения они остаются неизменными.
Положение некоторой произвольной точки М в системе координат звена i определяется вектором rMi , а в системе координат звена (i–1) – векто-
ром rMi−1 . Эти радиусы связаны между собой через матрицу преобразования координат Мi следующим уравнением:
rMi−1 = MirMi ,
где Mi – матрица перехода из i-й системы координат в (i – 1)-ю,
214
|
|
cosϕi |
− cosθi sin ϕi |
− sin ϕi sin θi |
ai |
cosϕi |
|
|
|
|
|
||||||
Mi |
= |
sin ϕi |
cosθi cosϕi |
− cosϕi sin θi |
ai |
sin ϕi |
|
. |
|
|
0 |
sin ϕi |
cosθi |
|
si |
|
|
|
|
0 |
0 |
0 |
|
1 |
|
|
Рассмотрим шестиподвижный манипулятор в исходном или начальном положении (рис. 8.6). За начальное положение принимается такое, в котором все относительные обобщенные координаты равны нулю. Переход из системы координат любого i-го звена к неподвижной (базовой) системе записывается в виде
rM0 = M1M2...MirMi или rM0 = ΤirMi ,
где Ti – матрица преобразования координат i-й системы в координаты базовой системы, Τi = M1M2...Mi .
Рис. 8.6. Кинематика шестиподвижного манипулятора: 0–6 – его звенья
Для схемы, изображенной на рис. 8.6, радиус rM6 = 0, а радиус rM0 определяется по формуле
rM0 = Τn = Τ6 ,
т.е. положение выходного звена манипулятора определяется матрицей Тn. Элементы этой матрицы назначают положение центра схвата (точки М) и ориентацию его в пространстве. Четвертый столбец дает декартовы координаты точки М (проекции вектора rM0 на оси координат). Третий столбец
215
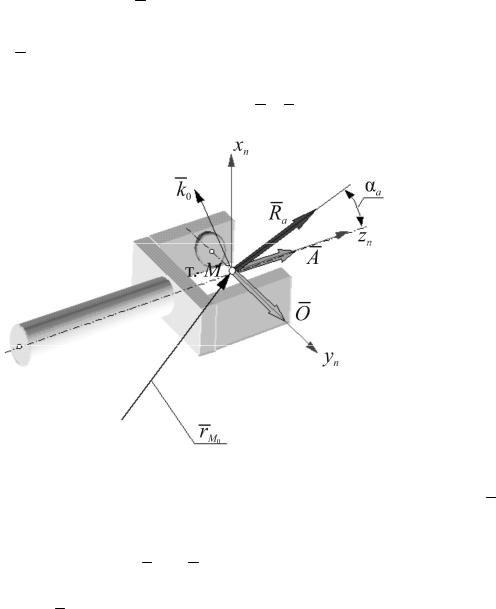
содержит направляющие косинусы оси zn системы координат, связанной со схватом, или вектора подхода A, который характеризует направление губок схвата (рис. 8.7). Второй столбец определяет направление оси yn или вектора ориентации O, который проходит через центр схвата по оси, перпендикулярной рабочим поверхностям его губок. В первом столбце содержатся направляющие косинусы оси xn или вектора (O × A).
Рис. 8.7. Кинематика схвата
Углом подхода схвата aA называется угол между вектором подхода A и базовым вектором:
RA = (O × κ0 ),
где κ0 – орт вектора z0 неподвижной или базовой системы координат. С учетом сказанного матрица Τn может быть представлена в следующем виде:
|
|
|
|
|
|
|
|
(O |
× A) |
||||
|
|
|
× |
|
) |
|
T = |
(O |
A |
||||
n |
|
|
|
|
|
|
(O × A) |
||||||
|
||||||
|
0 |
|
|
|||
|
|
|
|
|
|
|
x
y
z
Ox |
Ax |
rMxn |
|
Oy |
Ay |
rMyn |
. |
Oz |
Az |
rMzn |
|
0 |
0 |
1 |
|
|
|
|
|
В результате матричных преобразований получаем радиус-вектор точки М схвата в функции обобщенных координат. Обычно за обобщенные координаты принимают линейные и угловые перемещения в кинематических парах или на выходных валах приводов манипулятора. В механизме с n сте-
216