
2080
.pdf
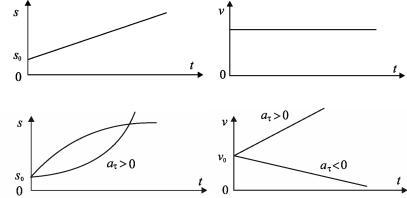
Основным условием равномерного движения является vτ = const, т.е. тангенциальное составляющее скорости остается постоянной во времени. Если при этом траектория движения представляет собой прямую линию, то движение будет прямолинейным и равномерным, если траектория кривая линия, то движение – криволинейное равномерное. Уравнением равномерного движения является:
уравнение скорости vτ = const; aτ = 0; уравнение пути s0 = s0 + v t.
Если за равные промежутки времени скорость тела или материальной точки изменяется на одинаковую величину, то такое движение называется равнопеременным. Если при этом траектория движения представляет собой прямую линию, то движение будет прямолинейным и равнопеременным, если траектория кривая линия, то движение – криволинейное равнопеременное. Уравнением такого движения является:
уравнение скорости v = v0 ± aτ t; уравнение пути s = s0 + v0 t ± aτ2t2 ;
aτ = const.
Графики скорости и пути для вышеуказанных движений приведены в табл. 1.1 (все таблицы в конце данной главы).
Проанализируем некоторые частные случаи движения:
1. aτ = 0; an = 0 . Так как aτ = dvτ 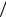 dt = 0, то vτ = const, зна-
dt = 0, то vτ = const, зна-
чит, движение равномерное. Если an = v2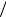 R = 0, так как v ≠ 0, то R →∞, значит, траектория движения − прямая линия. Таким об-
R = 0, так как v ≠ 0, то R →∞, значит, траектория движения − прямая линия. Таким об-
разом, в этом случае движение МТ равномерное и прямолинейное.
2. aτ = const , an = 0 . Если aτ = dvτ 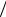 dt = const, то за равные промежутки времени скорость изменяется на одинаковую величину, значит, движение равнопеременное. При an = v2
dt = const, то за равные промежутки времени скорость изменяется на одинаковую величину, значит, движение равнопеременное. При an = v2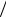 R = 0
R = 0
21
траектория движения представляет собой прямую линию. Таким образом, в данном случае МТ совершает прямолинейное равнопеременное движение.
3. aτ = 0 , an = const . Если aτ = dvτ 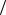 dt = 0, то движение рав-
dt = 0, то движение рав-
номерное. При an = v2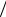 R = const, R = const траектория движения −
R = const, R = const траектория движения −
окружность. Значит, в данном случае МТ совершает равномерное движение по окружности.
4. aτ = 0 , an = f (t) . Если аn является функцией времени, то движение криволинейное. Так как aτ = 0 , то движение равно-
мерное. Таким образом, в данном случае МТ совершает равномерное криволинейное движение.
5. aτ = f (t) , an = f (t) . Если и тангенциальное, и нормальное
составляющие ускорения являются функциями времени, значит, движение неравномерное криволинейное.
1.3.Вращательное движение
Ккинематическим характеристикам вращательного движе-
ния относятся: |
ϕ – угол поворота; ϕ – вектор углового пере- |
мещения; ω – |
вектор угловой скорости; ε – вектор углового |
ускорения.
Вращательным движением твердого тела вокруг неподвижной оси называется движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения. Ось вращения перпендикулярна плоскостям, в которых лежат эти окружности. Она может проходить сквозь тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то те точки тела, которые лежат на этой оси, во время движения тела остаются в покое.
При вращательном движении абсолютно твердого тела нельзя пользоваться моделью материальной точки, ибо разные точки тела движутся по окружностям разного радиуса, т.е. их пути и скорости различны (рис. 1.4). В силу этой же причины
22
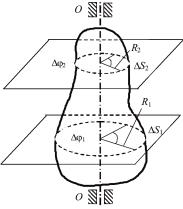
вращение твердого тела (как целого) не может быть охарактеризовано линейным перемещением и линейной скоростью, как это было сделано в поступательном движении. Вместе с тем, нетрудно заметить, что радиус-векторы, соединяющие все точки твердого тела с центрами описываемых ими окружностей, поворачиваются за один и тот же промежуток времени t на одинаковый угол ϕ (см. рис. 1.4). Следовательно, все точки абсо-
лютно твердого тела во вращательном движении проходят одинаковые угловые пути и имеют одинаковые угловую скорость и угловое ускорение. Поэтому в качестве кинематических характеристик вращательного движения тела должны быть выбраны вектор углового перемещения, угловая скорость и угловое ускорение.
Рис. 1.4
При малых поворотах тела угол поворота можно рассматривать как векторную величину dϕ , численно равную модулю
dϕ и направленную вдоль оси вращения OO′ так, чтобы из
конца вектора поворот тела был виден против часовой стрелки (правило буравчика) (рис. 1.5).
Угловой скоростью тела называют вектор ω , численно равный первой производной от угла поворота ϕ по времени и
23
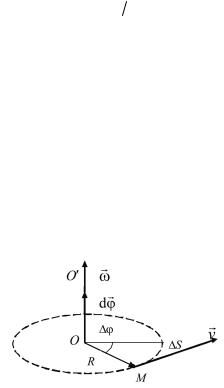
направленный вдоль оси вращения по правилу буравчика, т.е. так же, как вектор угла поворота:
|
(1.23) |
ω = dϕ dt. |
Угловая скорость характеризует направление и быстроту вращения тела как целого вокруг оси. Если ω = const, то движение тела называют равномерным вращением вокруг неподвижной оси.
Скорость v произвольной точки М тела, вращающегося с угловой скоростью ω , называют линейной скоростью этой точки. За время dt точка М проходит по дуге окружности радиусом R путь ds = vdt = Rsin∆φ, учитывая малую величину этого угла, можно записать ds = R∆φ или ds = Rdφ, поэтому
v = R |
dϕ |
= Rω. |
(1.24) |
|
dt |
||||
|
|
|
Рис. 1.5.
Из рис. 1.5 видно, что вектор v направлен перпендикуляр-
но и к ω , и к радиус-вектору R . Так как векторы R и ω взаимно перпендикулярны, то
|
|
|
= Rω = v. |
|
|
|
|
||
|
ω R |
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
(1.25) |
|
v |
= ω R. |
||
24
Так как в случае вращения тела вокруг неподвижной оси за начало координат, из которого проводят радиус-векторы r , можно выбрать любую точку оси вращения, то выражение (1.25) можно переписать в виде
v = ω r. |
(1.26) |
Для характеристики неравномерного вращения тела вводится понятие углового ускорения.
Угловым ускорением называют вектор ε , характеризующий быстроту изменения угловой скорости со временем и численно равный первой производной угловой скорости по времени:
|
(1.27) |
ε = dω dt. |
В случае вращения тела вокруг неподвижной оси изменение вектора ω обусловлено только изменением его числен-
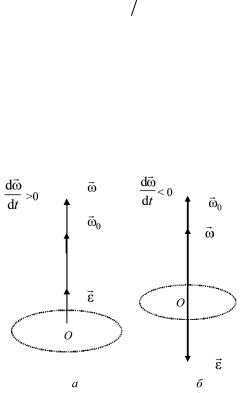
ного значения. При этом вектор ε направлен вдоль оси вращения (рис. 1.6): в ту же сторону, что и ω , при ускоренном вра-
щении (dω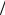 dt >0), в противоположную сторону − при замедленном вращении (dω
dt >0), в противоположную сторону − при замедленном вращении (dω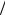 dt < 0).
dt < 0).
Рис. 1.6
25

Наряду с понятием угловой скорости пользуются понятиями периода и частоты вращения.
Периодом вращения Т называют промежуток времени, в течение которого тело совершает один полный оборот, т.е. поворачивается на угол 2π.
Частотой вращения n называют число оборотов, совершаемых телом за одну секунду.
Связь между ω, T и n имеет вид
ω = 2π T = 2πn. |
(1.28) |
Угол поворота в системе СИ измеряется в радианах (рад), угловая скорость − в радианах в секунду (рад/с), угловое ускорение − в радианах в секунду в квадрате (рад/с2).
Выразим тангенциальное и нормальное ускорение произвольной точки тела, вращающегося вокруг неподвижной оси, через угловую скорость и угловое ускорение тела:
aτ = ddvt = ddt (ωr) = r ddωt + ω ddrt = r ddωt + ωv = vrv = v v r = rε. (1.29)
Так как угол между линейными скоростями равен нулю, то синус угла между ними равен нулю и второй член в уравнении (1.29) равен нулю:
an = |
v2 |
2 |
r = |
4π2 |
r = 4π |
2 |
n |
2 |
r. |
(1.30) |
r |
= ω |
T 2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
Из рис. 1.7 и уравнения (1.29) следует, что вектор aτ равен
векторному произведению вектора углового ускорения ε на ра- диус-вектор r , соединяющий произвольную точку на оси вращения с точкой М:
aτ = ε r. |
(1.31) |
26
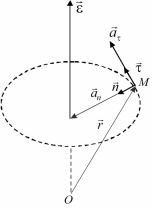
Вектор an нормального ус-
корения направлен к центру кривизны траектории вдоль внешней нормали, проведенной к рассматриваемой точке траектории:
|
= |
v2 |
(1.32) |
|
|
a |
|
n. |
|
||
n |
|
r |
|
|
|
|
|
|
|
|
|
В табл. 1.2 сопоставляются |
|
||||
характеристики и законы поступа- |
|
||||
тельного и вращательного движе- |
|
||||
ния материальной точки. Анали- |
|
||||
тическое и графическое описания |
Рис. 1.7 |
||||
этих двух видов движений анало- |
|
||||
гичные. Кроме того, в таблицах приводятся формулы, связывающие характеристики поступательного и вращательного
движений |
материальной точки. В табл. 1.3 |
даны единицы |
измерения |
кинематических характеристик |
поступательного |
и вращательного движений. |
|
|
1.4. Прямая и обратная задачи кинематики
Анализируя полученные формулы, в кинематике можно выделить четыре основных типа задач:
1. Общая прямая задача кинематики. По известной зави-
симости радиус-вектора от времени r (t) необходимо определить векторы скорости v и ускорения a, а также их модули v
и а, нормальную an и тангенциальную aτ составляющую уско-
рения, радиус кривизны траектории R.
2. Общая обратная задача кинематики. По известным век-
торам скорости v или ускорения a необходимо восстановить вид траектории, т.е. найти радиус-вектор r , а затем все остальные параметры траектории, указанные в п. 1.
27

3. Частная прямая задача кинематики. По известной зави-
симости пути от времени s(t) необходимо найти скорость v(t) и ускорение a(t) тела. В этом случае можно определить лишь модуль скорости и ускорения:
v = ddst и a = ddvt .
Векторы r , v, a, а также an , aτ в этих задачах не могут
быть определены.
4. Частная обратная задача кинематики. По известным зависимостям скорости v(t) или ускорения a(t) необходимо
восстановить зависимость пути от времени s(t) :
s = v(t)d(t), v = a(t)d(t).
Для вращательного движения прямая задача кинематики заключается в нахождении зависимости проекции угловой скорости на направление оси вращения ωz и проекции углового
ускорения на эту же ось εz по заданному как функция времени угла поворота ϕ = ϕ(t). Эта задача решается дифференцированием по времени:
ωz = ddϕt , εz = ddωtz .
Обратная задача: по заданному как функция времени угловому ускорению εz = εz (t) и начальным условиям ωz (t = 0) = ω0
и ϕz (t = 0) = ϕ0 найти кинематический закон вращения. Она решается с помощью интегрирования:
t |
|
t |
|
ωz (t) = ω0 + |
εz (t)dt, |
ϕ(t) = ϕ0 + |
ωz (t)dt. |
0 |
|
0 |
|
28
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 . 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Виды движения (уравнения и графики) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вид движения |
Уравнение |
|
График |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поступательное движение |
Равномерное |
|
s0 = s0 +vt; |
|
|
|
|
|
|
|||||||||||||
|
|
|
v =const; |
|
|
|
|
|
|
||||||||||||
|
|
|
|
aτ =0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Равнопеременное |
s = s |
0 |
+v |
0 |
t± |
|
aτ |
|
t2 |
; |
|
||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
v =v0 ± |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
aτ |
|
t; |
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
aτ =const |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неравномерное |
a |
|
|
= |
dv |
= |
d |
2 |
s |
|
|
– |
|||||||||
|
τ |
|
|
||||||||||||||||||
|
dt |
dt 2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
29
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончание табл. 1 . 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вид движения |
Уравнение |
|
График |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вращательное движение |
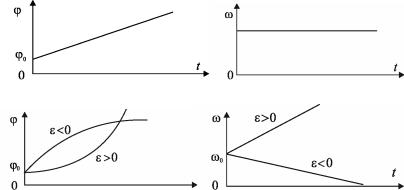
Равномерное |
ϕ= ϕ0 +ωt; |
|
|
|||||||||||||
|
ω= const; |
|
|
|||||||||||||
|
|
ε = 0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равнопеременное |
ϕ = ϕ0 +ω0 t ± |
|
ε |
|
|
t2 |
; |
|
||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
2 |
|
||||||||||||||
|
ω= ω0 ± |
|
ε |
|
|
|
|
|||||||||
|
|
|
t; |
|
|
|||||||||||
|
|
|
|
|
||||||||||||
|
ε = const |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Неравномерное |
ε = |
dω |
= |
d |
2 |
ϕ |
|
|
– |
|||||||
|
|
|
|
|
||||||||||||
|
dt |
dt2 |
|
|||||||||||||
|
|
|
|
|
||||||||||||
