
2080
.pdf
10.5. Основное уравнение молекулярно-кинетической теории (уравнение Клаузиуса) и следствия из него
Для вывода основного уравнения молекулярно-кинети- ческой теории (МКТ) рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически и число взаимных столкновений между молекулами газа намного
меньше, |
чем число ударов |
о стенки |
сосуда. Допустим, |
что столкновения молекул со стенками сосуда носят характер абсолютно упругого удара. Выделим на стенке сосуда некоторую элементарную площадку S (рис. 10.2) и вычислим давление, оказываемое на эту площадку.
При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс mivi –(–mivi) = 2mivi, где mi – масса i-й молекулы, vi – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме параллелепипеда с основанием S и высотой v t (см. рис.10.2). Число этих молекул N = nV = n Sv t (n = N/V – концентрация молекул, равная отношению числа молекул к объему занимаемого ими пространства).
Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул (1/6) движется вдоль данного направления в одну сторону, половина –
161

в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет равно 1/6 n Sv t. При столкновении с площадкой эти молекулы одинаковой мас-
сы передадут ей импульс |
P = 2mv1/6n |
Sv t = 1/3nm |
Sv2 |
t. |
|
Тогда давление газа, |
оказываемое им на стенку сосуда, |
||||
p = F S ; согласно второму |
закону |
Ньютона |
F = |
P t , |
|
поэтому |
|
|
|
|
|
p = |
P |
= 1nmv2 . |
|
(10.4) |
|
S t |
|
||||
|
3 |
|
|
|
|
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2, …, vN, то целесообразно рассматривать среднюю квадратичную скорость
vкв = |
1 |
vi2 , |
(10.5) |
|
N |
||||
|
|
|
характеризующую всю совокупность молекул газа. Уравнение (10.4) с учетом (10.5) примет вид
p = |
1nm v |
2 . |
(10.6) |
|
|
3 |
0 |
кв |
|
|
|
|
|
|
Выражение (10.6) называется основным уравнением моле- кулярно-кинетической теории идеальных газов или уравнением Клаузиуса. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.
Учитывая, что n = N V , получим
V , получим
pV = |
1 Nm vкв |
2 , |
|
(10.7) |
|||||
|
|
|
3 |
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
pV = |
N |
m vкв |
= |
Е, |
(10.8) |
||||
3 |
2 |
|
3 |
||||||
|
|
|
|
|
|
|
|||
162 |
|
|
|
|
|
|
|
|
|

где Е – суммарная кинетическая энергия поступательного движения всех молекул газа. Уравнение (10.8) является еще одной формой записи основного уравнения молекулярно-кинетической теории идеального газа.
Рассмотрим следствия, вытекающие из основного уравнения молекулярно-кинетической теории идеального газа:
1. Уравнение (10.8) позволяет получить все известные законы идеального газа: Гей-Люссака, Бойля–Мариотта, Шарля, Менделеева–Клапейрона и др. Действительно, если в сосуде объемом V при давлении р и температуре Т находится N молекул, то n = N/V, а Е = сТ в силу (10.3), где с – коэффициент пропорциональности. Тогда
p = 23 VN cT .
Коэффициент 2/3Nc = В зависит от массы газа и его природы. Если масса газа постоянна, то можно записать закон Кла- пейрона–Менделеева
pV |
= B = const. |
(10.9) |
|
T |
|||
|
|
В соответствии с законом Авогадро моли всех газов при нормальных условиях занимают одинаковый объем, равный 22,4 м3/моль. Отсюда следует, что в случае, когда количество газа равно 1 моль, величина В в (10.9) будет одинаковой для всех газов и ее можно обозначить буквой R и назвать универсальной газовой постоянной (R = 8,31 Дж/(К моль)). Тогда уравнение (10.9) для 1 моль запишется в виде
рVμ = RT. |
(10.10) |
От уравнения для 1 моль можно перейти к уравнению для любой массы газа, приняв во внимание, что при одинаковых давлении и температуре ν = M  μ моль будут занимать в ν раз
μ моль будут занимать в ν раз
больше объем, чем 1 моль, в результате получим
163
V = νV = |
M V , |
(10.11) |
|
μ |
μ |
μ |
|
|
|
|
|
где М – масса газа; μ – масса моля газа (молярная масса). С учетом (7.11), выражение (7.10) перепишем в виде
pV = |
M RT. |
(10.12) |
|
μ |
|
Уравнение (10.12) называется уравнением состояния идеального газа или уравнением Менделеева–Клапейрона для произвольной массы газа.
2. Так как, согласно второму закону Авогадро, моли всех газов содержат одинаковое число молекул, равное NA = = 6,02 1026 моль−1, уравнение (10.12) можно преобразовать к новому виду. Для этого введем величину k = R N A .
N A .
Подставив в выражение k численные значения R и NA, по-
лучим k = |
8,31 Дж/моль |
= 1,38 10−23 Дж/К (постоянная |
|
6,023 1023 моль−1 |
|||
|
|
Больцмана).
Умножив и разделив правую часть уравнения (10.12) на NA, получим
pV = νNAkT.
Произведение νNA равно числу молекул N, содержащихся в массе газа M. С учетом этого получим
pV = NkT,
а с учетом того, что N V = n − число молекул в единице объема, можно записать
V = n − число молекул в единице объема, можно записать
p = nkT. |
(10.13) |
Уравнение (10.13) показывает, что давление идеального газа при данной температуре определяется только числом молекул в единице объема и не зависит от рода молекул.
164
Из формулы (10.13) вытекает еще один справедливый для идеального газа закон – закон Дальтона для смеси газов.
Пусть имеется смесь нескольких не взаимодействующих друг с другом идеальных газов. Допустим, что в единичном объеме смеси содержится n1 молекул газа 1, n2 молекул газа 2 и т.д. Тогда общее число молекул в единичном объеме n = n1 + + n2 + … Согласно (10.13) давление газа определяется так:
p = nkT = (n1 + n2 |
+…)kT = |
(10.14) |
|
= n1kT + n2kT + … = p1 + p2 +…, |
|||
|
|||
где р1, р2, … – давления, которые оказывали бы газы этой смеси, если бы они заполняли объем по отдельности. Эти давления называются парциальными. В итоге закон Дальтона гласит: давление смеси идеальных газов равно сумме парциальных давлений газов, входящих в смесь, т.е.
р = р1 + р2 + … . |
(10.15) |
3. Газовые законы Бойля–Мариотта, Гей-Люссака и Шарля описывают равновесные изопроцессы в идеальном газе.
Изопроцессами называются равновесные процессы, при которых один из параметров состояния не изменяется. Различают изотермический (Т = const), изобарический (p = const), изохорический (V = const) и другие процессы.
Сформулируем законы для изопроцессов в идеальном газе, предполагая, что масса газа постоянна: М = const.
Изотермический процесс. Положив T = const, М = const, из уравнения Менделеева–Клапейрона (10.12) получим закон Бойля−Мариотта:
pV = const. |
(10.16) |
Если масса и температура идеального газа не изменяются, то произведение давления газа на соответствующий объем есть величина постоянная.
165
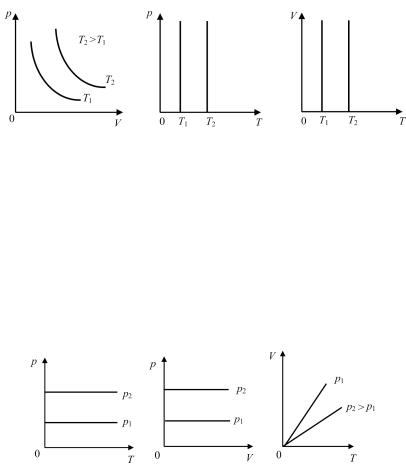
Графическое изображение изотермических процессов при двух разных температурах в координатах (p,V), (p,T) и (V,T) представлено на рис. 10.3.
Рис. 10.3
Изобарический процесс. Положив p = const и m = const, из уравнения (10.12) получим закон Гей-Люссака:
V / T = const. |
(10.17) |
Если в ходе процесса давление и масса газа не изменяются, то отношение объема газа к соответствующей абсолютной температуре остается постоянным.
Изобары, соответствующие двум разным давлениям, приведены на рис. 10.4.
Рис. 10.4
Изохорический процесс. Положив V = const и M = const, из уравнения (10.12) получим закон Шарля:
166
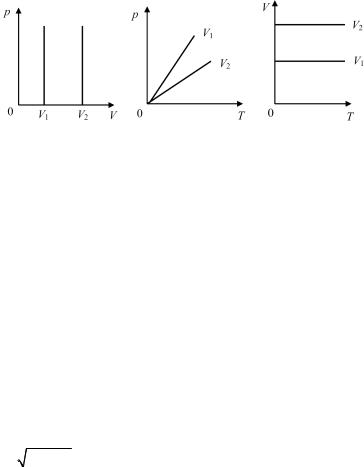
р / V = const. |
(10.18) |
Если в ходе процесса объем и масса газа не изменяются, то отношение давления газа к соответствующей абсолютной температуре есть величина постоянная.
Рис. 10.5
Изохоры, соответствующие двум разным объемам, приведены на рис. 10.5.
10.6. Закон Максвелла распределения молекул идеального газа по скоростям и энергиям
При выводе основного уравнения МКТ молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т.е. в любом направлении в среднем движется одинаковое количество молекул.
Согласно молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул газа массой М в газе, находящемся в состоянии равновесия при T = const, остается постоянной
 vкв
vкв = 3kT
= 3kT M . Это объясняется тем, что в газе, находящемся
M . Это объясняется тем, что в газе, находящемся
в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, подчиняющееся вполне определенному закону. Этот закон теоретически выведен Дж. Максвеллом.
167

Максвелл предполагал, что газ состоит из большого числа N тождественных молекул (они находятся в состоянии хаотического теплового движения при одинаковой температуре) и что силовые поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до
v+dv, т.е. dN (v)/ N = f (v)dv, откуда f (v)=dN (v)/ Ndv.
Применяя методы теории вероятностей, Максвелл нашел функцию f(v) – закон для распределения молекул идеального газа по скоростям:
|
M 3 2 |
|
2 |
|
− m0v2 / (2kT ) |
|
|
|
f (v) = 4π |
|
|
v |
|
e |
|
. |
(10.19) |
|
|
|
||||||
|
2πkT |
|
|
|
|
|
|
|
Из (10.19) видно, что конкретный вид функции зависит от рода газа (масса молекулы) и от параметра состояния (температура Т).
График функции (10.19) приведен на рис. 10.6. Так как при
возрастании скорости v множитель e− mv2 (2kT ) уменьшается быстрее, чем растет множитель v2, то функция f(v), начинаясь с нуля, достигает максимума при наиболее вероятной скорости vв и затем асимптотически стремится к нулю. Кривая несимметрична относительно vв.
(2kT ) уменьшается быстрее, чем растет множитель v2, то функция f(v), начинаясь с нуля, достигает максимума при наиболее вероятной скорости vв и затем асимптотически стремится к нулю. Кривая несимметрична относительно vв.
Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь полоски на рис. 10.6. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки
∞
f (v)dv =1.
0
168

Рис. 10.6
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью vв. Значение наиболее вероятной скорости можно найти, продифференцировав выражение (10.19) (постоянные множители опускаем) по аргументу v, приравняв результат к нулю и использовав условие для максимума выражения f(v):
d |
(v2e− mv2 (2kT ) )= 2v 1− mv2 |
e− mv2 (2kT ) = 0. |
|
|
|||
dv |
|
2kT |
|
Значения v = 0 и v = ∞ соответствуют минимумам выражения (10.19), значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость vв:
vв = 2kT / m = 2RT / M . |
(10.20) |
Из формулы (10.20) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 10.7) смещается вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.
169

|
|
Рис. 10.7 |
|
|
|
|
|
|
|
|||
Средняя скорость молекулы |
|
v |
(средняя арифметическая |
|||||||||
скорость) определяется по формуле |
|
|
|
|
|
|
|
|||||
|
1 |
∞ |
|
|
∞ |
|
|
|
|
|
|
|
v = |
|
vdN(v) |
= vf (v)dv. |
|
|
|||||||
|
|
|
||||||||||
|
N 0 |
|
|
0 |
|
|
|
|
|
|
|
|
Подставляя в последнее выражение f(v) и интегрируя его, |
||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
v = 8kT / (πm) = |
8RT / (πM ). |
(10.21) |
||||||||||
Скорости, характеризующие состояние газа (см. рис. 10.6): |
||||||||||||
1) наиболее вероятная vв = 2RT / M ; |
|
|
|
|
||||||||
2) средняя v = 8RT / (πM ) =1,13vв; |
|
|
|
|
||||||||
3) средняя квадратичная vкв = |
3RT / M =1,22vв. |
|
||||||||||
Исходя из распределения молекул по скоростям |
|
|||||||||||
|
|
|
m |
3/2 |
2 |
|
− mv2 |
/ |
2kT |
|
|
|
dN (v) = N 4π |
|
|
v |
|
e |
|
( |
|
)dv, |
(10.22) |
||
2πkT |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
можно найти распределение молекул газа по значениям кинети-
ческой энергии |
ε. Для этого перейдем |
от переменной v |
к переменной ε |
= mv2/2. Подставив в |
уравнение (10.22) |
v = 2ε m и dv = (2mε)−1 2 dε, получим |
|
|
170 |
|
|
