Математическое моделирование в естественных науках.-1
.pdf
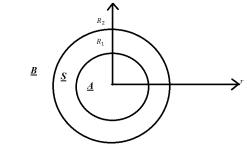
Рис. Иллюстрация к постановке задачи
Математическая модель включает три уравнения диффузии (для разных областей):
ρA |
∂CA |
= |
|
|
1 ∂ |
2 |
DAρA |
∂CA |
, |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|||||||||||||
∂t |
|
|
|
r |
2 |
|
|
|
|
|
|
∂r |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ρ |
|
|
∂Cs |
|
= |
1 |
|
|
|
|
∂ |
r2 D |
ρ |
|
∂CS |
|
, |
|
|
|
|
|||||||||||||
S |
|
|
|
|
|
2 |
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
||||||||||||||
|
∂t |
|
|
|
|
r |
|
|
|
|
|
|
|
S |
|
|
∂r |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ρ |
|
|
∂CB |
|
= |
|
|
1 |
|
|
|
|
∂ |
r |
2 D |
|
ρ |
|
∂CB |
, |
|
|
||||||||||||
B |
|
|
|
|
|
|
|
2 |
|
|
|
|
B |
|
|
|
|
|
|
|||||||||||||||
|
∂t |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
B |
|
|
|
∂r |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
– граничные условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
r = 0 : ∂CA = 0, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r = R |
: D |
|
|
|
∂CA = D |
∂CS ,C |
|
|
= γ |
|
|
C |
|
, |
||||||||||||||||||||
|
1 |
|
|
A |
|
∂r |
|
|
|
|
|
|
|
|
S |
|
∂r |
|
|
|
|
A |
|
|
A |
|
S |
|
||||||
r = R |
: D |
|
∂CS = D |
∂CB ,C |
|
|
= γ |
|
C |
|
, |
|||||||||||||||||||||||
|
2 |
|
|
S |
|
∂r |
|
|
|
|
|
|
|
|
B |
|
∂r |
|
|
|
|
S |
|
|
|
S |
|
B |
|
|||||
– и начальные условия:
t = 0 : CA = 1, CS = 0, CВ = 0.
625