Математическое моделирование в естественных науках.-1

μ(φ) = δδφF = f '(φ) + 2 2φ+ 4φ.

Здесь F – функционал свободной энергии для расчетного домена Ω , который можно записать следующим образом:

Решение PFC-уравнения – задача, требующая использования специальных алгоритмов [2] и применения высокопроизводительной вычислительной техники. Поэтому для решения (1) был разработан специальный численный вычислительный алгоритм [3], использующий библиотеки PETSc и PETIGA [4], написанные на языке С++. Библиотеки предоставляют набор примитивов и подпрограмм для разработки масштабируемых, эффективных и распараллеливаемых алгоритмов. Чтобы оценить качество разработанного метода, в настоящей работе выполнена серия вычислительных экспериментов, главной целью которых явилась оценка эффективности распараллеливания алгоритма.

Первая серия экспериментов проводилась на гомогенном кластере. Использовалось 5 вычислительных узлов, соединенных сетью Infiniband QDR 40 GB/sec. Каждый узел состоял из двух 14-ядерных процессоров Intel E5-2697 v3, с 64GB RAM.

В каждом эксперименте программа рассчитывала задачу в течение одного шага времени.

В первом эксперименте исследовалась зависимость сложности задачи от количества конечных элементов. Использовался фиксированный домен 160×160×160 (1603) и 5 узлов, включаю-

щих 28 ядер на каждом узле. Размер сетки устанавливался в 103, 203, 403, 803, 1603.

Во втором эксперименте исследовалась эффективность распараллеливания при изменении количества вычислительных узлов. Домен фиксирован – 1603. Размер сетки фиксирован – 503.

521

Количество узлов менялось от 1 до 5. На каждом узле работало по 28 ядер.

Втретьем эксперименте рассматривалась зависимость эф-

фективности распараллеливания при изменении вычислительных ядер. Использовались фиксированный домен (1603) и сетка – (503). Менялись количество ядер от 1 до 28, использовался один вычислительныйузел.

Входе экспериментов кластер показал производитель-

ность, соответственно: 4.45E+9, 3.68E+9, 8.03E+8 Flops/sec.

Впервом эксперименте размер используемой памяти, общее количество операций и общее количество MPI сообщений росли экспоненциально с одинаковой скоростью при уменьшении размера ячейки вычислительной сетки. Во втором эксперименте размер используемой памяти и общее количество MPI сообщений практически не изменялись с увеличением количества узлов. Общее количество операций немного уменьшалось, что само по себе требует дальнейшего изучения. Вычислительное время уменьшалось логарифмически с ожидаемой скоростью. В третьем эксперименте зафиксирована большая вариативность в размере используемой памяти – этот эффект также требует дальнейшего изучения. Изменчивость в общем количестве операций и общем количестве MPI-сообщений коррелирует

сизменчивостью размера используемой памяти. Вычислительное время уменьшалось ожидаемым образом.

Была проведена оценка балансировки нагрузки. В первом эксперименте разброс по памяти составил 40 %, по количеству операций – 60 %. Эти показатели характеризуют сложность задачи балансировки вычислений на мелкой сетке. Во втором экс-

перименте по памяти – 20 %, по количеству операций – 35 %. В третьем эксперименте, соответственно – 28 и 55 %.

Вторая серия экспериментов проводилась на гетерогенном кластере. Были подготовлены две группы специальных тестовых задач:

522

1-я группа: Расчеты на 1 вычислительном узле. В данном случае одна и та же задача запускалась на процессоре Tesla k40. Количество потоков, которые обрабатывались одновременно, варьировалось от 1 до 20.

2-я группа: Расчеты на 3 вычислительных узлах, включающих по 1 карте Tesla k40. Одна и та же задача запускалась сначала на 1 вычислительном узле, затем на 2 и, наконец, на 3.

Вторая серия экспериментов показала, что разработанный алгоритм может быть распараллелен для расчетов на GPU NVIDIA Tesla, но прирост производительности при увеличении количества вычислительных потоков быстро уменьшается. Было установлено, что подключение дополнительных видеокарт не дает существенного прироста вычислительной мощности. Кроме того, рост накладных расходов, увеличение нагрузки на коммуникационные интерфейсы и ухудшение параметра балансировки могут приводить даже к падению производительности.

Настоящая работа выполнена при частичной поддержке Российского научного фонда, проект 16-11-10095.

Список литературы

1.Galenko P.K., Danilov D.A., Lebedev V.G. Phase-field-crystal and Swift-Hohenberg equations with fast dynamics // Physical Review. – 2009. – E 79 (5). – 051110.

2.Unconditionally stable method and numerical solution of the hyperbolic phase-field crystal equation / P. Galenko, H. Gomez, N. Kropotin, K. Elder // Phys. Rev. – 2013. – E 88 (1). – 013310.

3.Bueno J., Starodumov I., Gomez H., Galenko P., Alexandrov D. // Computational Materials Science. – 2016. – 111. – 310–312.

4.Collier N., Dalcin L., Calo V.M. Petiga: high-performance isogeometric analysis: preprint arXiv: 1305.4452. – 2013.

523

ИССЛЕДОВАНИЕ ТЕЧЕНИЯ ЖЕЛЧИ В ЖЕЛЧЕВЫВОДЯЩИХ ПУТЯХ С УЧЕТОМ ВЗАИМОДЕЙСТВИЯ «ЖИДКОСТЬ – ТВЕРДОЕ ТЕЛО»

М.А. Перетягин, А.Г. Кучумов

Пермский национальный исследовательский политехнический университет,

Пермь, Россия, peretyaginmisha@gmail.com, kychymov@inbox.ru

В данной работе представлено исследование течения желчи (как неньютоновской жидкости) в протоках (как гиперупругого материала) желчевыделительной системы человека. Представлено решение задачи течения желчи с учетом взаимодействия «жидкость–твердое тело» в индивидуализированной геометрии желчных протоков реального пациента с использованием параметров желчи и стенок протоков, взятых из эксперимента.

Ключевые слова: желчь, желчевыводящие пути, неньютоновская жидкость, взаимодействие «жидкость–твердое тело».

Желчные заболевания, такие как холелитиаз (желчнокаменная болезнь) и холецистит (воспаление желчного пузыря), во многих случаях влекут за собой удаление желчного пузыря. На сегодняшний момент патологии билиарной системы находятся на третьем месте по частоте заболеваний среди взрослого населения в России (число пациентов в России – около 10 миллионов человек). Ежегодно появляется около 200 000 новых больных. Количество операций, которые осуществляются в медицинских учреждениях, является недостаточным для того, чтобы покрыть растущую потребность в них со стороны пациентов. Число осложнений также велико (около 5000 человек погибают от осложнений холелитиаза), поскольку хирурги не всегда могут спрогнозировать исход операции, основываясь лишь на субъективном опыте. Например, как изменилось функциональное восстановление организма (суточный расход желчи, давление и т.д.) в пост-операционный период врач предугадать не может.

Для того чтобы понять причины заболеваний, важно осуществить физиологическое и механическое описание поведения билиарной системы человека в целом и её отдельных составляющих [1].

524

Вданной работе проводится исследование течения желчи

внорме и при патологии. Предварительно был проведен эксперимент по исследованию реальных свойств желчных протоков путём установления зависимости зависимости между перемещением стенок и приложенным внутренним давлением (эксперимент на раздувание). С помощью аппроксимации зависимости и оптимизационной процедуры были найдены параметры определяющего соотношения (неогуков потенциал). Свойства желчи взяты из работы [2]. Далее осуществлялось пошаговое исследование индивидуализированной модели желчных протоков пациента. На начальном этапе было проведено МРТ исследование брюшной полости пациента и, основываясь на полученных данных, была построена геометрическая модель протоков в программном пакете SolidWorks. Далее с помощью программного пакета ANSYS WORKBENCH была решена задача течения жел-

чи в желчевыводящих путях с учетом взаимодействия «жидкость – твердое тело». Найдены распределения скоростей и давлений желчи в желчевыводящих путях, а также распределение сдвиговых напряжений в стенках протоков. Данный подход может считаться эффективным инструментом в диагностике и лечении желчекаменной болезни.

РаботавыполненаприподдержкегрантаРФФИ 16-08-00718.

Список литературы

1.One-dimensional models of the human biliary system / W.G. Li, X.Y. Luo, A.G. Johnson, N.A. Hill, N. Bird, S.B. Chin // ASME J. Biomech. Eng. – 2007. – Vol. 129. – P. 164–173.

2.Биомеханический подход к моделированию билиарной системы как шаг в направлении к построению виртуальной модели физиологии человека / А.Г. Кучумов, Ю.И. Няшин, В.А. Самарцев, В.А. Гаврилов, М. Менар // Российский журнал биомеханики. – 2011. – Т. 15, №2. – С. 64–76.

525

ОБОБЩЕННАЯ ДИНАМИЧЕСКАЯ МОДЕЛЬ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ПРОСТРАНСТВЕННЫМИ ШАРНИРАМИ

А.А. Поляков, Ар.А. Поляков, И.Ю. Остаточников, А.В. Конюшевский

Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, Екатеринбург, Россия, a.a.polyakov@urfu.ru, i.u.ostatochnikov@gmail.com, Alias-free@ya.ru

Рассматриваются вопросы исследования динамики привода рабочего органа, представляющего собой многосвязанную систему с пространственными шарнирами, используемую в различной технике, и, в частности, очистных машинах [1]. Исследовано влияние на динамические нагрузки углов перекоса шарниров, приведённых моментов инерции, угловых скоростей, жесткостей звеньев, технологических моментов. Определены динамические коэффициенты и установлены зоны резонансов для различного сочетанияпараметровсистемы.

Ключевые слова: динамическая модель, механическая система, динамическая нагрузка, система с пространственными шарнирами, зоны резонансов, динамические параметры, упругие колебания.

Шарнирные механические передачи и состоящие из них системы нашли широкое применение в технике, однако теория их недостаточно изучена, в особенности пространственных систем. Например, в приводах исполнительного органа очистных машин [1, 2] используются пространственные шарнирные механические системы.

При определённых соотношениях статических и динамических параметров в приводе с пространственными шарнирами могут возникнуть неустойчивые состояния, сопровождающиеся повышением уровней упругих колебаний, параметрические колебания и параметрический резонанс, оказывающие существенное влияние на нормальный режим работы оборудования и эксплуатационную надёжность. Поэтому исследование динамических явлений в шарнирных системах представляет большой научный

ипрактический интерес для установления рациональных режимов

исозданияв конечномитоге надёжнойи экономичной техники.

526

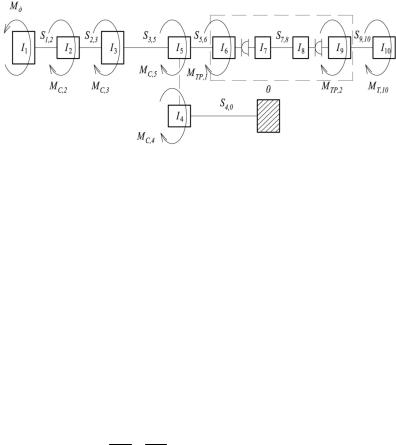
Характерная такой системе динамическая модель представлена на рис. 1, которая учитывает влияние на динамический процесс всех основных факторов: кинематической особенности шарниров, статических и динамических параметров системы.

Рис. 1. Динамическая модель рабочего органа

Динамическая модель описывается системой нелинейных дифференциальных уравнений, полученной на основе использования квазистатического способа, при непосредственном применении принципа Даламбера, где приняты следующие обозначения: M∂ – момент на двигателе, Ii – момент инерции i-го элемента системы Si,j – жёсткость i, j-го вала, Mc,i – момент вязкого трения в элементах i-й массы, MTP,i – момент трения в i-м пространственном шарнире, MT,I – технологический момент, приложенный к i-й массе.

После преобразования данной системы к виду, удобному для компьютерной обработки с помощью численного метода интегрирования Рунге – Кутта, уравнения системы имеют вид:

ψ1 = Mд − S1,2 (ψ1 − ψ2 ) − b1,2 (ψ1 − ψ2 );

I1 I1

527

щие явную кинематическую связь с углами поворота (i – 1) массы [рад]; K j,i − коэффициенты пропорциональности между величи-

ной потерь внутреннего трения в упругой связи, выраженной в размерности момента, и величиной относительной скорости перемещения масс [Hмс]; Fi – кинематические функции.

Кинематические функции (Fi), входящие в уравнения (1), зависятоттипамеханическойшарнирнойпередачииеёпараметров.

528

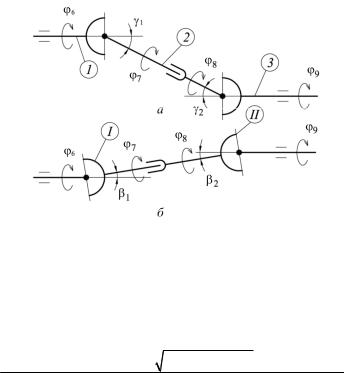
Так, для одной из линий привода рабочего органа (выделенной на рис. 1 пунктирным прямоугольником) механическая шарнирная передача включает три звена (5,6; 7,8; 9,10), связанных между собой двумя универсальными шарнирами. Подробно фрагмент этой передачи приведен на рис. 2.

Рис. 2. Пространственная двухшарнирная передача

Применительно к выделенному фрагменту (см. рис. 2) кинематические функции F1 и F2 соответствуют случаю, когда оси всех валов расположены в разных плоскостях (γ1 ≠ 0, γ2 ≠ 0, β1 ≠ 0, β2 ≠ 0), имеют аналогичный вид, в частности, для F1:

Анализ результатов динамических нагрузок и влияния различных факторов на поведение динамической системы показал, что существует возможность для рекомендации по выбору параметров системы, при которых динамические нагрузки имеют минимальные значения и исключается риск возникновения резонансов в системе.

529

Список литературы

1.Устройство для очистки наружной поверхности трубопроводов: а.с. № 1814934 / Поляков А.А., Артемкин А.А., Ба-

тюшев Э.С. – 1993. – Бюл. № 18.

2.Способ очистки полимерных покрытий с поверхности трубопроводов: пат. Рос. Федерация. № 2060006 / Поляков А.А., Батюшев Э.С., Житков В.В., Артемкин А.А., Бирюков Н.М. – 1996. – Бюл. № 16.

3.Поляков Ар.Ал., Поляков Ал.Аф. Динамические нагрузки в механической системе исполнительного механизма очистной машины // Изв. ВУЗов. Нефть и газ. – Тюмень: Изд-во ТюмГНГУ, 2003. – № 6. – С. 61–66.

ИССЛЕДОВАНИЕ НЕУПРУГОГО ДЕФОРМИРОВАНИЯ СТАЛИ С УЧЕТОМ МАРТЕНСИТНЫХ ПЕРЕХОДОВ

Л.Е. Попкова, Н.Д. Няшина

Пермский национальный исследовательский политехнический университет,

Пермь, Россия, lidiadom@mail.ru; nnd73@perm.ru

Сформулирована и поставлена задача для мартенситного перехода под действием нагрузок и изменения температуры на макро- и мезоуровне. Реализован соответствующий вычислительный алгоритм для кристаллита стали, который подвергается нагрузке и изменению температуры. Предложенный алгоритм использован для отображения количества мартенсита со временем. Полученные результаты являются этапом в построении двухуровневой математической модели, описывающей твердотельные мартенситные фазовые переходы, происходящие в сталях при термомеханической обработке.

Ключевые слова: мартенситный переход, движущие силы, трансформационныесистемы.

Современный мир сложно представить без использования сталей. Для различных деталей необходимы разные заданные свойства, которые получают путем изменения структуры сталей с сохранением у изделия формы и химического состава. Для

530