Надежность систем автоматизации

Определим h(t)∆t – вероятность того, что отказ произойдет в интервале ∆t при условии, что перед этим отказов не было в течение времени t, по формуле условной вероятно-

сти [6]:

Для экспоненциального распределения

h(t) = λe−λt = λ,

e−λt

т.е. функция опасности есть интенсивность отказов.

Опыт эксплуатации показывает, что h(t) = λ изменяется следующим образом (рис. 2.8):

λ

Рис. 2.8. Изменение λ при эксплуатации технических объектов

I. 1-й период повышенных интенсивных отказов. Это период приработки, что связано с выявлением дефектов при изготовлении.

41

II. 2-й период, характеризующий постоянные значения интенсивных отказов. Это участок нормальной эксплуатации изделия.

III. 3-й период, характеризующий повышенную интенсивность отказов. Здесь начинается процесс старения.

Период приработки преодолевают путем предварительной «тренировки», испытаний и ускоренных испытаний перед началом эксплуатации.

С другой стороны, моральный износ аппаратуры наступает раньше периода старения. Это дает основания считать интенсивность отказов величиной постоянной и равной на всем периоде эксплуатации, т.е. пользоваться экспоненциальным законом распределения:

P(t) = e−λt ≈1−λt, F(t) =Q(t) ≈ λt.

2.5. Распределение Вейбулла – Гнеденко

Распределение предложено шведским ученым Вейбуллом для моделирования прочности сплавов и обосновано математически советским ученым Б.В. Гнеденко (1912–1995) – советским математиком, специалистом по теории вероятностей, математической статистике, вероятностным и статистическим мето-

дам (рис. 2.9).

Основными параметрами распределения Вейбулла – Гнеденко являются [4, 5] λ0 – масштаб кривой по оси абсцисс и α – острота и асимметрия распределения. Обычно берут 1 ≤ α ≤ 2. При α = 1 распределение Вейбулла – Гнеденко переходит в экс-

Рис. 2.9. Б.В. Гнеденко поненциальное.

42

Рис. 2.10. Распределение Вейбулла – Гнеденко для различных α:

а – Р; б – f; в – λ

Примерный вид соответствующих кривых дан [4, 5] на рис. 2.10. С таким распределением хорошо согласуется время безотказной работы качественных полупроводниковых приборов.

2.6.Нормальное распределение (распределение Гаусса)

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний.

Карл Фридрих́ Гаусс́ (нем. Johann Carl Friedrich Gauß, 1777– 1855) – выдающийся немецкий математик, астроном и физик, считается одним из величайших математиков всех времен [2] (рис. 2.11).

Дед Гаусса был бедным крестьянином, отец – садовником, каменщиком, смотрителем каналов в герцогстве Брауншвейг. Уже в двухлетнем возрасте у мальчика проявились невероятные умственные способно-

43

сти. В три года он умел читать и писать, даже исправлял счетные ошибки отца. Согласно легенде школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1 + 100 = 101, 2 + 99 = 101 и т.д., и мгновенно получил ре-

зультат 50 · 101 = 5050. До самой старости он привык большую часть вычислений производить в уме.

Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение – отсюда и произошло одно из его названий.

Нормальный закон является предельным, к которому приближается ряд других законов при весьма часто встречающихся типовых условиях. Значения параметров соответствуют значениям среднего математического ожидания и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием, равным 0, и стандартным отклонением, равным 1. Плотность вероятности нормального распределения изображена на рис. 2.12.

Функция распределения вероятности нормального закона представлена на рис. 2.13.

Функция распределения Гаусса имеет вид [6]

где – среднее, σ – дисперсия, это N( , σ2).

44

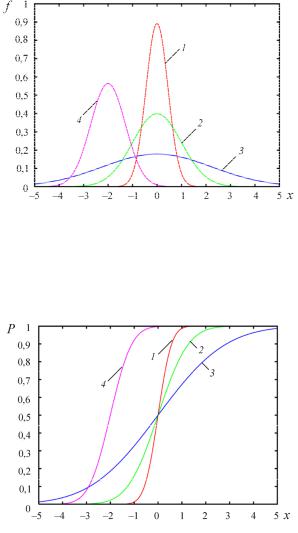
Рис. 2.12. Плотность вероятности распределения Гаусса: 1 – µ = 0, σ2 = 0,2; 2 – µ = 0, σ2 = 1,0, линия соответствует стандартному

нормальному распределению – «колокол»; 3 – µ = 0, σ2 = 5,0; 4 –

µ = –2, σ2 = 0,5

Рис. 2.13. Функция распределения вероятности Гаусса: 1 – µ = 0, σ2 = 0,2; 2 – µ = 0, σ2 = 1,0, 3 – µ = 0, σ2 = 5,0; 4 – µ = –2, σ2 = 0,5

45

σ

Этот интеграл не выражается через элементарные функ-

ции.

Интеграл вероятностей

Интеграл вероятностей вычисляется по специальным таблицам [4, 5], тогда

Свойства интеграла вероятностей Ф:

Ф(0) = 0; Ф(+∞) = 12 ; Ф(−x) = −Ф(x).

При нормальном (гауссовом) распределении случайной величины ось абсцисс имеет протяженность от –∞ до +∞. Поскольку время t не может быть отрицательной величиной, в теории надежности используется усеченное нормальное распределение.

Основными параметрами для нормального распределения являются Т – среднее значение наработки на отказ, σt – среднеквадратическое отклонение.

46

циальной таблице [4, 5].

f(t) = θ t σ−T .

t

Значения θ(и) приведены в специальной таблице [4, 5].

На рис. 2.14 [4, 5] представлен примерный вид кривых Р, λ, f нормального распределения.

P, λ, f P(t) λ(t)

f(t)

t

Рис. 2.14. Примерный вид соответствующих кривых нормального распределения

Нормальное распределение может использоваться при исследовании надежности объектов, отказы которых обу-

47

Агнер Краруп Эрланг (1878–1929) – датский математик, статистик, инженер, основатель научного направления по изучению трафика в телекоммуникационных системах и теории массового обслуживания (рис. 2.15). Эрлангом была получена формула для расчета доли вызовов, получающих обслуживание на сельской телефонной станции.

В табл. 2.1, 2.2 приведены сводные данные по основным непрерывным Рис. 2.15. А.К. Эрланг и дискретным распределениям теории

надежности (в табл. 2.1 – дискретные распределения теории надежности, в табл. 2.2. – непрерывные).

Таблица 2.1

49