Надежность систем автоматизации

т.е., например, три образца проработали 2 ч, а к 4-му часу они не «дотянули». Время измеряется дискретно:

T = ((2 ч) 3 + (4 ч) 3 + 6 5 + 8 8 + 10 7 + 12 6 + 14 2 + 16 1)/35 ≈ ≈ 8,52.

Дисперсия

Dt = (6,522 3 + 4,522 3 + 2,522 5 + 0,582 8 + 1,482 7 + 3,482 6 + + 5,482 2 + 7,482)/35 ≈ 12,193.

Находим σt = 12,193 ≈ 3,49.

31

2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН, ИСПОЛЬЗУЕМЫЕ В ТЕОРИИ НАДЕЖНОСТИ

Вместо характеристик надежности объекта, заданных в виде таблицы, используют специальные формулы, получаемые по результатам эксперимента. Иными словами, подбирают такую формулу (функцию), которая наиболее удачно подходит в данном случае, и определяют коэффициенты этой формулы.

Наиболее типичные формулы называются законами распределения случайных величин.

2.1. Равномерное распределение

Пример равномерного распределения представлен на рис. 2.1.

F(t)

1

Равномерное распределение (R) – своего рода простейшее распределение. Оно используется для приближенных вычислений показателей надежности при малых t.

32

2.2.Биномиальное распределение

Впроцессе испытаний на надежность нас может интересовать только факт того, произойдет некоторое событие или нет. Пусть р – вероятность успеха (1 – работает), а q – вероятность неудачи, q = 1 – р (0 – отказ). При m успехах в n экспериментах получим m единиц и (n – m) нулей. При независимости результатов отдельных успехов вероятность этой последовательности будет иметь вид [6]

pmqn−m = pm (1− p)n−m.

Общее число последовательностей из n элементов, содержащих m единиц и (n – m) нулей, число сочетаний из n по m,

В отличие от равномерного распределения – это дискретное распределение.

Функция плотности распределения: m единиц и (n – m)

нулей в n экспериментах. Поскольку все эти последовательности несовместимы (если появилась одна, то появление любой другой исключено), то вероятность одной из них

тогда получим

f (2;3;0,9) =3 0,81 0,9 = 0,243 = Р2.

33

Числовыми характеристиками биномиального распределения являются среднее значение νm = np и дисперсия

σ2m = npq = np(1− p).

Рис. 2.2. Вид биномиального распределения вероятностей для различных m при p = 0,8, n = 10

Биномиальное распределение обозначают иногдаВ(m, n, p) (рис. 2.2).

2.3. Распределение Пуассона

Значения биномиальных коэффициентов f = (m, n, p) неудобно вычислять при больших n. Одним из путей упрощения вычислений является замена биномиального распределения на распределение Пуассона [6] (рис. 2.3).

Рис. 2.3. Симеон-Дени Пуассон

(фр. Siméon-Denis Poisson, 21 июня

1781–25 апреля 1840 гг.) – знамени-

тый французский физик-математик

34

Найдем предел функции f = (m, n, p) при n→∞, p→0

причем в числителе 2-й дроби – m элементов. Например, для

следнего при n →∞ выражения равен 1. Также и при любом m

35

является то, что среднее значение и дисперсия одинаковы и равны а.

Распределение Пуассона является хорошим приближением к биномиальному распределению при малых значениях, например при р < 0,01 с n = 10.

Распределение Пуассона является самостоятельным классом стохастических процессов, называемых классом редких случайных явлений.

Рассмотрим последовательность событий S, следующих друг за другом через равные промежутки времени [6]. Число таких событий, происходящих на интервале времени длительностью t, будет случайной величиной со средним значением λt, где λ – среднее число событий за единицу времени.

Поставим задачу определить вероятность того, что на интервале t произойдет ровно m событий. События S – редкие в смысле того, что интервал времени длительностью t можно разбить на малые интервалы ∆t, в каждом из которых может произойти не более одного события. Общее число интерва-

лов n = ∆tt . Вероятность того, что событие произойдет в од-

Поскольку можно считать, что на каждом интервале событие происходит независимо от событий в других интервалах, мы приходим к процессу независимых испытаний с распределением вероятностей f (m,n, p). Это оправдано только

36

в том случае, когда ∆t → 0. При этом n →∞, p →0. Получаем

f (m,λt) = (λt)m e−λt , m!

функцию плотности вероятности распределения Пуассона

(рис. 2.4).

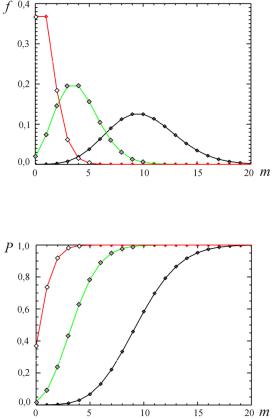
Рис. 2.4. Плотность вероятности для распределения Пуассона: – λ = 1; – λ = 4; – λ = 10

Рис. 2.5. Функция распределения вероятности Пуассона. Обозначения см. рис. 24

На рис. 2.5 показана функция распределения вероятностей P(m, λ).

37

2.4. Экспоненциальное распределение

ет, что при малых λt можно пренебречь вероятностью наступления на интервале t более двух событий [6]. При этом вероятность наступления на интервале t одного события

F(λ,t) =1−e−λt , t ≥ 0.

38

Функция распределения вероятностей приведена на рис. 2.6.

Рис. 2.6. Функция распределения вероятности экспоненциального распределения: – – – λ = 0,5;

λ = 1,0; ––– λ = 1,5

Функция плотности вероятностей приведена на рис. 2.7.

Рис. 2.7. Функция плотности вероятности экспоненциального распределения:

– – – λ = 0,5; λ = 1,0; ––– λ = 1,5

39

По существу, выражение F(λ,t) =1−e−λt , t ≥ 0 – вероят-

ность того, что время, за которое произойдет одно событие, не превысит t [6]. Тогда плотность распределения для этой вероятности, представляющей собой вероятность того, что событие произойдет в момент t, получим, продифференциро-

вав F [6]:

dF(λ,t) = λe−λt . dt

Вероятность того, что не произойдет ни одного события,

P(λ,t) = e−λt .

Среднее время, за которое не произойдет ни одного события,

Полученные выражения определяют экспоненциальное распределение, имеющее важное значение в теории надежно-

сти [6].

Некоторое устройство состоит из большого числа отдельных элементов, каждый из которых с течением времени может перейти в состояние отказа. В большинстве случаев отказы независимы друг от друга и их последовательность может быть рассмотрена как процесс независимых событий, в котором λ определяет число отказов в единицу времени и называется интенсивностью отказов, а величина 1/λ – среднее время безотказной работы. Размерность λ – час в ми-

нус первой степени (ч–1).

Для характеристики надежности аппаратуры иногда используют показатель опасности отказа h(t), выражающий плотность распределения вероятности отказа в момент t при условии, что до этого момента отказов не было.

40