Физические основы микро- и нанотехнологии

Два электрона эквивалентны, если у них одинаковые и одинаковые l. Поэтому согласно принципу Паули два эквивалентных электрона должны отличаться другот друга направлением либо спина, либо l.

Принцип Паули существенно усложняет рассмотрение энергетических состояний более сложных атомов или энергетических состояний электронов в кристаллах. Например, если атом имеет систему энергетических состояний, сходную со спектром атома кислорода, то на низшем энергетическом уровне могут располагаться только два электрона, поскольку этот уровень двухкратно вырожден. Третий электрон должен располагаться уже на следующем, более высоком уровне. После того как и этот уровень заполнится, последующие электроны должны переходить на еще более высокие уровни. Развитие технологии наноэлектроники привело к тому, что, казалось бы, столь далекий от реальной жизни принцип Паули работает в таком сугубо прагматическом приборе, как атомно-силовой микроскоп, при помощи которого можно наблюдать за отдельными атомами.

1.2.5. Волновая функция

Необходимость вероятностного подхода к описанию каждой из элементарных частиц относится к любым процессам в микромире и является одной из важнейших отличительных особенностей квантовой теории. Можно ли истолковать волны де Бройля непосредственно как волны вероятности, т.е. правильно ли считать, что вероятность обнаружения микрочастицы в разных точках пространства меняется по волновому закону? Нет, поскольку если вероятность меняется по волновому закону, то тогда вероятность обнаружения частицы для некоторых точек пространства примет отрицательные значения, что противоречит ее смыслу.

Эти трудности можно устранить, если принять, что по волновому закону меняется не сама вероятность, а некая величина, названная амплитудой вероятности и обозначаемая обычно Ψ(x, y, z). Эту

величину называют также волновой функцией. Амплитуда вероятности должна быть комплексной, а вероятность ω должна быть пропорциональна квадрату ее модуля:

21

ω≈ Ψ 2 .

Волновая функция выступает в квантовой теории как основной носитель информации и о корпускулярных, и о волновых свойствах системы. Вероятность нахождения частицы в элементе объема

dω= Ψ 2 dV ,

поэтому величину Ψ 2 называют плотностью вероятности (т.е. ве-

роятностью, отнесенной к единице объема). Предложенное Максом Борном толкование волн де Бройля исключает их понимание как классических волн материи. Связывая со свободным электроном плоскую волну, не следует это понимать (по Борну), что электрон будто бы «размазан» по огромной области. Это означает то, что, хотя электрон и продолжает выступать в теории как точечный объект, вероятность обнаружения его в любой из точек пространства одинакова.

Описывающая состояние квантовой частицы волновая функция Ψ не может быть непосредственно измерена, хотя выражающиеся через Ψ физические величины являются объектами экспериментальных исследований.

По установившейся терминологии некоторое математическое действие, производимое над величиной, рассматривается как результат применения к этой величине определенного оператора. В квантовой механике, как правило, встречаются линейные и квадратичные зависимости от импульса. Квадрат оператора понимается как знак двухкратно повторенного действия этого оператора. Как и в любой теории, дающей вероятностное описание, сопоставление с опытом производится для средних значений физических величин. В квантовой механике вводится важный постулат: каждой физической величине, выражаемой в классической механике ввиде определенной функции F(x, y, z, px, py, pz) координат и импульсов,

ставится в соответствие оператор F (x, y, z, lpx , lpy , lpz ). Такое сопостав-

ление операторов с классическими величинами является общей специфическойчертойквантования.

22

Если действие оператора lA на волновую функцию Ψ равносильно ее умножению на некоторое число a, то Ψ называют собственной функцией оператора, а число а – его собственным значением:

lA Ψ = aΨ.

Конкретному оператору соответствует определенное множество собственных функций и собственных значений. Совокупность собственных значений называют их спектром. Таким образом, наблюдаемые на опыте значения физических величин и есть собственные значения для операторов соответствующих величин. Это положение считается настолько важным, что его часто рассматривают как отдельный постулат квантовой механики.

Если собственные значения меняются плавно (непрерывно), т.е. могут пробегать любые промежуточные значения, то их спектр называют непрерывным. Однако наиболее интересным и специфичным именно для квантовой теории является существование дискретных спектров, которые нельзя объяснить на основе классической физики. Появление такой дискретности обусловливается чаще всего видом операторов физических величин и граничными условиями.

1.2.6. Уравнение Шредингера

Важнейшим является спектр собственных значений оператора

l

полной энергии H. Для одной частицы в заданном внешнем потенциальном поле оператор полной энергии, называемый оператором Гамильтона или гамильтонианом,

l = l + l

H T U (x, y, z),

где Tl – оператор кинетической энергии;

l

U – оператор потенциальной энергии частицы.

Уравнение для его собственных функций Ψ и собственных значений ε имеет вид

23

Это одно из основных уравнений квантовой механики, называемое уравнением Шредингера для стационарных состояний.

Конкретизируя в каждой из рассматриваемых задач физическую природу и особенности взаимодействия, можно установить зависимость потенциальной энергии U от координат. Решение уравнения (1.1) при учете граничных условий дает весь набор собственных значений и соб-

l

ственных функций оператора H , т.е. все возможные значения энергии физической системы. При этом для состояний, которые отвечают так называемому финитному движению, т.е. движению частиц в ограниченной области пространства, спектр значений энергии получается дискретным. Если область, в которой могут быть обнаружены частицы, неограниченно велика, то энергия может меняться непрерывно.

Переход к анализу состояний позволяет не анализировать при-

и пространству. Предполагается, что именно эти усредненные значения параметров состояния и фиксируются в экспериментальных исследованиях, поэтому их использование в уравнениях позволяет описывать реальные явления.

При одной и той же форме оператора потенциальной энергии

l

U (x, y, z) спектры могут быть как дискретными, так и сплошными

(непрерывными). Так, электронные состояния в кулоновском поле атомного ядра могут иметь как дискретный, так и непрерывный энергетические спектры. Первый соответствует классическому движению по эллиптическим орбитам, второй – движению по незамкнутым параболическим или гиперболическим орбитам. Какой из этих вариантов реализуется, определяется значением энергии.

Обычно функция Ψ(х, t) определяется из выражения для плотности вероятности нахождения частицы в точке х в момент времени t.

Плотностьвероятности = Ψ*(x,t )Ψ(x,t ).

В общем случае Ψ – величина комплексная. Ввиду того, что вероятность должна быть величиной действительной, для нахождения плотности вероятности необходимо умножить Ψ на комплексно со-

24

пряженную с ней функцию Ψ*(x,t ). Поскольку Ψ*(x,t )Ψ(x,t )dx,

есть вероятность того, что частица находится в интервале от х до (x + dx) в момент времени t и поскольку вероятность нахождения частицы в какой-либо точке пространства в некоторый момент времени t равна единице, то

∫−∞∞ Ψ*(x,t )Ψ(x,t )dx =1.

Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов Ньютона, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее правило для нахождения Ψ в частных физических задачах. Таким уравнением является уравнение Шредингера. В одномерном случае оно имеет вид

где h – постоянная Планка; m – масса частицы;

U(x) – потенциальная энергия частицы в точке х.

Уравнение (1.2) записано в одномерном представлении для упрощения.

Уравнение Шредингера дается без какого-либо вывода и вообще не может быть выведено из более простых представлений, точно так же, как не могут быть выведены из каких-либо простых законов законы Ньютона. Уравнение Шредингера является просто законом физики, и если оно имеет смысл, то должно приводить к правильному предсказанию экспериментальных данных. Квантовая теория не требует полного отказа от законов Ньютона, а лишь настаивает на отказе от абсолютной определенности в задании начальных условий. Если размер и масса частицы становятся макроскопическими, то предсказания квантовой и классической теории совпадают друг с другом, потому что неопределенный путь частицы становится близким к однозначной траектории.

25

Форма уравнения Шредингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда U не является функцией времени, можно записать в виде

где функция Ψ(x) должна удовлетворять (в одномерном случае) уравнению

Уравнение (1.4) вообще не содержит такого параметра, как время, поэтому оно называется уравнением Шредингера, не содержащим времени. Выражение (1.3) является лишь частным решением зависящего от времени уравнения Шредингера (1.1). Зависимость функции Ψ(x, t ) от времени проста, но зависимость ее от координа-

ты не всегда имеет элементарный вид, так как уравнение (1.4) при одном выборе вида потенциальной функции U(x, t) совершенно отличается от того же уравнения при другом выборе этой функции. В действительности уравнение (1.14) может быть решено аналитически лишь для небольшого числа частных типов функции U(x).

Важное значение имеет интерпретация величины Е в уравнении (1.3). Она производится следующим путем: временная зависимость функции Ψ(x,t) в уравнении (1.3) имеет экспоненциальный характер,

причем коэффициент при t в показателе экспоненты выбран так, что правая часть уравнения (1.4) содержит только постоянный множитель Е. В левой части уравнения (1.4) функция Ψ умножается на потенциальную энергию U(x). Следовательно, величина Е должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся)

26

энергия системы. Таким образом, можно предполагать, что величина E представляет собой полную энергию системы. Согласно физической интерпретации уравнения Шредингера Е действительно является полной энергией частицы при движении, описываемом функцией Ψ(x,t).

1.2.7. Волновые функции свободных частиц

Можно попытаться получить решение уравнения Шредингера для случаев, когда известно силовое поле, характеризующееся потенциальной функцией U(x). Как и при использовании законов Ньютона, простейшая ситуация складывается в случае, когда сила, действующая на частицу, равна нулю. Предположим, что U(x) = 0 и исследуем уравнение Шредингера. Уравнение (1.3) принимает вид

Уравнение (1.5) оказывается чрезвычайно простым, поскольку оно имеет тот же вид, что и уравнение, описывающее гармонический осциллятор, если время в этом уравнении заменить на х. Решениями такого уравнения является синус или косинус некоторого аргумента, однако по ряду соображений более удобна экспоненциальная форма. Одним из решений (но не самым общим) является функция вида

а зависящая от времени Ψ-функция приобретает вид

Функция (1.6) описывает бегущую волну. Для подтверждения того, что функция (1.6) носит характер бегущей волны, рассмотрим струну, колеблющуюся со смещением в направлении у, которое определяется из выражения

y = ei(kx−ωt) .

27

Смещение струны в момент времени t равно eikx, т.е. выражается синусоидой с длиной волны λ = 2πk . Движение точки в начале координат х = 0 описывается выражением eiωt, которое также представляет собой синусоиду с периодом t = 2πω. Постоянная k назы-

вается вектором распространения или волновым вектором, а ω – угловой частотой. Очевидно, что в другой момент времени в другой точке колебание струны также является синусоидальным, но его фаза сдвинута относительно фазы первоначального колебания. Волна распространяется вдоль струны со скоростью V = ω / k, поскольку в момент времени t смещение (или фаза), существовавшее в точке х = 0 при t = 0, сместилось в точку x =ωtk .

Функция Ψ в уравнении (1.6) имеет тот же вид, что и волна в струне, и, таким образом, можно прийти к выводу, что волновая функция для частицы представляет собой бегущую волну. Этот вывод является полезным сам по себе, но, кроме того, с помощью простых преобразований из формулы (1.6) можно получить два очень важных соотношения. Запишем сначала эту формулу в виде

Ψ = ei(kx−ωt) ,

где

Здесь частота ω выражается через энергию системы. Постоянная k является также функцией энергии:

k = 8π2mE h.

Представим k в другом виде. Энергия в рассматриваемом случае является кинетической энергией U (x)= 0 , следовательно,

E = p2 2m, где р – импульс частицы. Таким образом,

28

Соотношение (1.7), называемое соотношением Эйнштейна, и соотношение (1.8), называемое соотношением де Бройля, устанавливают, что движение частицы носит волновой характер. Они представляют концепцию корпускулярно-волнового дуализма. Сущность его можно выразить следующим образом. Волновая функция электрона, если на него не действуют силы, представляет собой бегущую синусоидальную волну, но если электрон каким-либо образом обнаруживается в действительности, то он обнаруживается как реальная и вполне локализованная частица.

1.2.8. Квантование энергии. Частица в потенциальном ящике

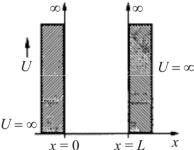
Из уравнения Шредингера можно вывести одно из фундаментальных положений квантовой механики – положение о квантовании энергии. Рассмотрим одномерное движение частицы, ограничив это движение пределами ящика: 0 ≤ x ≤ L. Пусть потенциальная энергия бесконечна при х< 0 их> 1 иравнанулюпри 0 ≤ x ≤ L (рис. 1.1). УравнениемШредингерадля

29

Поскольку в точке х = 0 косинус не равен нулю, тогда как синус обращается в нуль, Ψ-функция должна быть синусоидальной. Решение необходимо ограничить также рассмотрением лишь таких синусоидальных функций, которые обращаются в нуль при х > L.

Аналитически требование, налагаемое на функцию в точке х = L, выражается следующим образом:

Согласно уравнению (1.9) k может принимать не все значения; разрешенными значениями являются лишь те, для которых выполняется условие

k = nLπ, n =1, 2, …, ∞.

Если волновой вектор k может пробегать лишь последовательность дискретных значений, то энергия частицы также дискретна, т.е. она квантуется:

Смысл выражения (1.10) заключается в том, что частица, движущаяся в потенциальном ящике, может обладать не произвольным значением энергии, а лишь одним значением из набора дискретных значений. Энергия, таким образом, обладает дискретным спектром, который показан на рис. 1.2. Причину того, что энергия совершенно свободной частицы не квантована, можно легко понять, проанализировав выражение (1.10). Если длина потенциального ящика бесконечно увеличивается, то расстояние между энергетическими уровнями становится бесконечно малым. В общем случае, согласно квантовой механике, несвязанные частицы, которые можно считать практически свободными, имеют непрерывный энергетический спектр, тогда как частицы, которые удерживаются какими-либо силами в конечной области пространства, обладают дискретным энергетическим спектром.

30