
Прикладная теория колебаний
..pdf
Раскрывая определитель по первой строке и группируя члены, получим кубическое уравнение относительно ω2:
|
|
|
|
m1 +m2 |
|
|
m2 +m3 |
|
|
|
m1 +m2 |
+ m3 |
|
|
|
|
|
ω2 |
ω4 |
c |
+c |
|
|
ω2 |
+ |
c c |
|
= 0. |
(3.7) |
||||||
m m |
2 m m |
m m m |
|||||||||||||||
|
|
|
1 |
|
|
|
|
1 2 |
|
|
|
||||||
|
|
|
1 2 |
|
2 3 |
|
1 2 |
3 |
|
|
|
|
|||||
Рассматриваемая система из трех масс имеет три комбинации взаимных продольных смещений, что следует из решения уравнения (3.7), поэтому и существуют три частоты и формы колебаний.
Одна из частот ω32 = 0, а это физически означает, что все
три массы перемещаются как единое целое.
Две других комбинации получаются из решения биквадратного уравнения
|
|
|
|
ω2 |
= |
1 |
|
m +m |
+c |
m +m |
|
± |
|
|
|
||||||||
|
|
|
|
|
c |
|
1 |
2 |
|
2 |
3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
m1m2 |
m2m3 |
|
|
|
|||||||||||||
|
|
|
|
1,2 |
|
2 |
1 |
|
2 |
|
|
|
|
|
|||||||||
± |
1 |
|
|
|
m |
+m |
+c |
|
m |
+ m |
2 |
−c c |
m |
+ m |
+m |
|
|||||||
|
c |
|
1 |
|
2 |
|
2 |
|
|
3 |
|
1 |
|
2 |
3 |
, |
(3.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
1 m1m2 |
|
2 m2m3 |
|
|
1 2 |
|
|
m1m2m3 |
|
|||||||||||
где ω1, ω2 – частота 1-го и 2-го тона соответственно.
3.1.2. Определение форм колебаний
Формы колебаний необходимо определять: во-первых, для выяснения мест максимальных деформаций, а следовательно, мест максимальных динамических напряжений; во-вторых, для определения максимальной величины самой деформации – самих динамических напряжений.
При рассмотрении трехмассовой системы мы выяснили, что каждая масса находится в двух колебательных и в одном поступательном движении (относительно неподвижной системы координат) как единое целое.
71
Стр. 71 |
ЭБ ПНИПУ (elib.pstu.ru) |

Общее решение системы:
x1 = A1,1 sin (ω1t +ϕ1 ) + A1,2 sin (ω2t +ϕ2 ) + A0 , |
|
|
|
||||||||
|
|
|
|||||||||
x |
= A |
sin (ω t +ϕ ) + A |
sin (ω t +ϕ |
2 |
) + A |
, |
|
(3.9) |
|||
2 |
2,1 |
1 |
1 |
2,2 |
2 |
|
0 |
|
|
|
|
x |
= A |
sin (ω t +ϕ ) + A |
sin (ω t +ϕ ) + A , |
|
|
||||||
3 |
3,1 |
1 |
1 |
3,2 |
2 |
2 |
0 |
|
|
|
|
|
|
|
|||||||||
где Аi,j – амплитуда колебаний i-й массы при j-й частоте. Значения Аi,j, ϕj определяются из начальных условий, на-
пример, из перемещений и колебательной скорости V в момент времени t = 0:
x3 t=0 = 0; x3 t=0 =V.
При построении форм колебаний важно найти соотношения между амплитудами масс для каждой частоты. Для этого используют систему алгебраических уравнений (3.5), подстав-
ляя в нее |
ω1 вместо ω (ω= ω1 ), |
и определяют соотношения |
||
A1,1 / A2,1 и |
A3,1 / A2,1, затем подставляют ω2 |
вместо ω (ω= ω2 ) |
||
и определяют A1,2 / A2,2 и A3,2 / A2,2. |
|
|
|
|
Выполним это для частоты ω1: |
|
|
||
|
2 |
0, |
|
|
|
(c1 −m1ω1 ) A1,1 −c1 A2,1 = |
|
|
|
|
−c1 A1,1 +(c1 +c2 −m2ω12 ) |
A2,1 −c2 A3,1 |
= 0, |
|
|
−c2 A2,1 +(c2 −m3ω12 ) A3,1 |
= 0. |
|
|
|
|
|
||
|
|
|
|
|
Поскольку два уравнения являются линейно зависимыми, то можно определить лишь соотношения амплитуд, т.е. решить систему с точностью до постоянной, полагая
A |
1 |
(или |
A |
1,0 |
для ω2). |
|||||
2,1 |
|
|
|
2,2 |
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
A1,1 = |
|
c1 |
|
A2,1; |
A3,1 = |
|
c2 |
|
A2,1. |
|
c −m ω2 |
c −m ω2 |
|||||||||
1 |
1 |
1 |
|
|
2 |
3 |
1 |
|
||
72 |
|
|
|
|
|
|
|
|
|
|
Стр. 72 |
ЭБ ПНИПУ (elib.pstu.ru) |
Аналогично для ω= ω2:
A1,2 = |
|
c1 |
|
A2,2 ; |
A3,2 = |
|
c2 |
|
A2,2. |
c −m ω2 |
c −m ω2 |
||||||||
1 |
1 |
2 |
|
2 |
3 |
2 |
|
||
На основании вычислений строят формы колебаний соответственно при колебаниях с частотой ω1 и ω2.
3.2. Расчет поперечных колебаний конструкций
3.2.1. Энергетический способ определения частот собственных поперечных колебаний конструкции
Для расчета частот поперечных колебаний примем следующие допущения:
–конструкцию представляем балкой с постоянной осредненной изгибной жесткостью (EJ )cp = const = EJ;
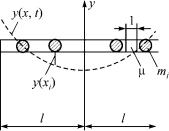
–конструкцию представля-
ем в виде распределенной постоянной погонной массы µ, а по длине будем полагать, что имеется ряд сосредоточенных масс грузов mi (рис. 3.2).
Точность расчетов 5–10 %. Суть метода заключается в использовании закона сохранения энергии системы при условии пренебрежения энергией рассеивания за счет внутреннего трения
в среде, т.е. при условии равенства максимальной потенциальной энергии деформации балки и максимальной кинетической энергии балки при колебаниях:
Wmax = Kmax .
73
Стр. 73 |
ЭБ ПНИПУ (elib.pstu.ru) |

При свободных поперечных колебаниях балки ее прогиб y(x, t) можно записать в виде произведения двух функций:
y (x, t ) = y (x)sin ωt.
При этом прогибе в сечениях балки возникает изгибающий момент
M = EJ |
d 2 y |
. |
(3.10) |
|
dx2 |
||||
|
|
|
Потенциальная энергия деформации балки длиной L = 2l определяется в основном энергией изгиба, т.е.
Wmax = 12 |
∫l |
Mdx = 12 |
∫l |
M |
1 |
dx = 12 |
∫l |
EJ ( y′′)max2 dx, (3.11) |
R |
||||||||
|
0 |
|
0 |
|
δ |
0 |
|
|
а кинетическая энергия определяется энергией конструкции и сосредоточенных масс:
Kmax = 12 |
∫l |
µ( y)max2 dx + 12 ∑mi |
( yi2 )max2 = |
|
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
ω2 l |
µy |
2 |
dx + |
∑ |
m y |
2 |
|
(3.12) |
||||||||||
|
2 |
|
∫ |
max |
|
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
i |
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где учтено условие, |
|
что sin ωt = ±1,0, |
|
а при максимальной ки- |
|||||||||||||||
нетической энергии cos ωt = ±1,0. |
|
|
|
|
|
|
|
|
|
||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
EJ y′′ |
|
(x) 2 dx |
|
|
|
||||||||
ω2 = |
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
, |
(3.13) |
||
l |
µ[y(x)]2 dx + |
∑ |
|
|
|
|
|
||||||||||||
|
∫ |
m |
|
y |
(x) 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
i |
1 |
|
max |
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где y(x) – форма изгиба при колебаниях. Она определяется граничными условиями опирания балки.
74
Стр. 74 |
ЭБ ПНИПУ (elib.pstu.ru) |

Приближенность формулы заключается в степени представления формы изгиба. Точность расчета ω зависит от точности представления формы изгиба для конкретного случая.
Например, для шарнирного опирания с постоянной массой и жесткостью без грузов mi
|
(x) = Asin |
nπx |
|
nπ 2 |
EJ |
|
|||
yn |
|
, ωn |
= |
|
|
µ |
, |
||
L |
L |
||||||||
|
|
|
|
|
|
||||
где n – номер тона, n = 1, 2, 3…
При произвольных условиях опирания имеем:
ω = |
k |
EJ |
, |
(3.14) |
|
L2 |
m |
||||
n |
|
|
где k – коэффициент, зависящий от схемы опирания конструкции, при шарнирном опирании k = nπ, для свободной балки
k= 2n2+1 π.
3.2.2.Расчет частот поперечных колебаний металлоконструкций при переменных конструктивных
параметрах
Для примера рассмотрим колебания стрелы крана
(рис. 3.3).
Рис. 3.3. Динамическая модель конструкции стрелы крана
75
Стр. 75 |
ЭБ ПНИПУ (elib.pstu.ru) |
Осредненную погонную массу конструкции µcp и изгибную жесткость (EJ)cp представляем в следующем виде:
µ |
|
= |
1 |
(m +m +m +m ), |
(3.15) |
||
cp |
|
||||||
|
|
L |
1 |
|
2 3 4 |
|
|
|
|
|
|
|
|
|
|
|
|
(EJ )cp = |
1 |
∑(EJ )i li , |
(3.16) |
||
|
|
L |
|||||
|
|
|
|
|
|
|
|
где L – длина стрелы; li – длина i-го участка; (EJ)i – изгибная жесткость i-го участка; mi – сосредоточенные массы, i = 1, 2, 3, 4.
Можно принять:
– для 1-го тона колебаний
y (x) = A cos |
πx |
; |
|
|
|||
1 |
1 |
0,552L |
|
|
|
|
|
– для 2-го тона колебаний
y |
|
(x) = A cos |
πx |
. |
2 |
|
|||
|
2 |
0,736L |
||
|
|
|
||
Тогда
|
|
|
|
|
|
|
ω2 |
= |
(EJ )cp |
× |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
µcp L4 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.17) |
|||
|
|
|
|
|
|
|
0,552 |
|
|
|
|
|
|
|
||||||||||||
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||
|
|
|
|
2 |
|
|
|
|
|
∑ |
|
|
|
m |
|
|
π |
|
x |
|||||||
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
cos2 |
|
|
|
i |
|
|||||
|
|
0,552 |
|
π |
|
|
|
|
|
µcp L |
0,552 |
|
||||||||||||||
|
|
+ |
|
|
|
|
|
i |
|
|
|
|
L |
|||||||||||||
|
|
1 |
π |
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0,552 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ω2 |
= |
(EJ )cp |
× |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
µcp L4 |
|
|
|
|
|
|
|
|
|||||||
76
Стр. 76 |
ЭБ ПНИПУ (elib.pstu.ru) |
|
|
|
|
|
|
|
|
2π |
4 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
× |
|
|
|
|
|
|
0,736 |
|
|
|
|
|
|
|
|
. (3.18) |
||||||
|
|
|
|
2 |
|
|
|
|
∑ |
|
|
m |
|
|
|
x |
||||||
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
i |
sin2 |
|
736 |
i |
|
||||
|
|
0,736 |
|
2π |
|
|
i µcp |
L |
|
|||||||||||||
|
|
+ |
|
|
|
|
|
|
|
L |
||||||||||||
|
|
1 |
2π |
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,736 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3.2.3. Меры борьбы с вредными влияниями вибраций
Борьба с вибрациями конструкций – очень сложная задача. Это объясняется большим разнообразием колебаний и причинами их возникновения, а также тем, что частоты собственных колебаний изменяются при работе.
Среди мер борьбы с вибрациями получили распространение следующие [6]:
1)отстройка от резонанса путем изменения конструкции, т.е. изменения ее жесткости или массы;
2)уменьшение амплитуд возникающих сил;
3)постановка демпферов;
4)изменение места расположения гидроцилиндров либо установка фильтров в систему управления.
4.ДИНАМИЧЕСКИЕ НАГРУЗКИ НА КОНСТРУКЦИЮ ПРИ БЫСТРОМ ИЗМЕНЕНИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
При решении многих практических задач вынужденные и собственные колебания конструкции сводятся к колебаниям системы с одной степенью свободы. Например, при продольных колебаниях могут быть:
– колебания конструкции при выгрузке грунта;
77
Стр. 77 |
ЭБ ПНИПУ (elib.pstu.ru) |

– колебания 2-массовой конструкции при запуске двига-
теля;
– продольные колебания конструкции при резкой остановке.
4.1. Расчет коэффициентов динамичности при спаде усилия
Рассмотрим случай динамического воздействия при запуске и выключении двигателя, полагая, что сила изменяется по линейному закону. При спаде усилия различают три участка
(рис. 4.1):
I. P(t) = P;
II.P(t) = P 1− t , где Т1 – время спада усилия;
T1
III. P(t) = 0.
Рис. 4.1. Характер изменения |
Рис. 4.2. Двухмассовая |
нагрузки |
динамическая модель |
|
системы |
Составим уравнение движения 2-массовой системы, к которой мы условно приводим данную задачу (рис. 4.2). Для этого умножим первое и второе уравнение на коэффициенты, указанные справа от системы уравнений, и из первого уравнения вычтем второе:
78
Стр. 78 |
ЭБ ПНИПУ (elib.pstu.ru) |
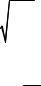
|
m1x1 = −cx1 +cx2 |
|
|
× |
|
|
|
m2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
m + m |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|||
|
m2 x2 = −cx2 +cx1 − P(x) |
× |
|
|
m1 |
|
|
|
|
|
|||||||||
|
m1 |
+ m2 |
|
|
|
|
|
||||||||||||
|
––––––––––––––––––– |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
m1m2 |
|
(x1 − x2 ) +c(x1 − x2 ) = P(t) |
|
|
|
m1 |
. |
|||||||||||
|
|
|
|
|
m |
|
|||||||||||||
|
m +m |
|
|
|
|
|
|
|
|
|
|
|
|
|
+m |
||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|||
После преобразований получим: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
mпр∆x +c∆x = P(t) |
|
|
|
|
m1 |
, |
|
|
||||||||
|
|
|
|
m1 + m2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где mпр – приведенная масса, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
m = |
m1m2 |
|
|
; |
|
|
|
|
|
|
|
|||||
|
|
|
m +m |
|
|
|
|
|
|
|
|
||||||||
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
∆x – динамические перемещения, |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
∆x = (x1 − x2 ). |
|
|
|
|
|
|
|
|||||||||
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
∆x +ω2∆x = P(t) |
|
|
, |
|
|
|
|
|
||||||||
|
|
|
m |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω= |
|
c |
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
|
||
На первом участке реализации усилия ∆x = 0, тогда
ω2∆xст = mР2 .
Статическое перемещение
∆xст = |
P |
|
1 |
= |
P |
|
|
m1 |
|
|
|
|
|
. |
|||||
ω2 |
m |
c |
m + m |
||||||
|
|
|
2 |
|
|
|
1 |
2 |
|
(4.1)
(4.2)
(4.3)
(4.4)
(4.5)
79
Стр. 79 |
ЭБ ПНИПУ (elib.pstu.ru) |

На втором участке
∆x +ω2∆x = P 1− |
1 |
|
1 |
. |
(4.6) |
|
|
||||
|
T1 |
|
m2 |
|
|
При начальных условиях |
|
|
|
|
|
∆x t=0 = ∆xст; ∆x t=0 = 0.
Общее решение дифференциального уравнения
|
|
∆x = A2 cosωt + B2 sin ωt + ∆xст 1− |
t |
. |
|
(4.7) |
|||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
|
|
||
Здесь А2, В2 определяются из начальных условий на втором |
|||||||||||||||||||||
участке. С учетом t = 0 запишем: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
∆x |
|
t=0 = ∆xст = A2 +∆xст(1−0). |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
Отсюда А2 = 0. Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∆x |
|
t=0 = 0 = −ωA2 sin ωt + B2ωcos0 +∆xст − |
1 |
. |
(4.8) |
||||||||||||||||
|
|||||||||||||||||||||
T1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда B2 |
= ∆xст . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ωT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При подстановке А2, В2 в уравнение (4.7) получим: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
∆x = ∆xст 1− |
+ |
sin ωt |
. |
|
|
(4.9) |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
T1 |
ωT1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На третьем участке |
∆x +ω∆x = 0, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.10) |
||||||
|
|
|
∆xII |
|
|
= ∆x |
sin ωt ∆xIII |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
t=T1 |
ст ωT1 |
|
t=0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
∆x = A3 cosωt + B3 sin ωt, |
|
|
|
|
|
|
||||||||||||
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стр. 80 |
|
|
|
|
ЭБ ПНИПУ (elib.pstu.ru) |
|
|
|
|
|
|
|
|
||||||||
