Прикладная теория колебаний

5.2. Характеристики распределения. Среднее значение и моменты

При исследовании случайной переменной величины важно знать ее значение, вокруг которого группируется основная масса вероятностей. С точки зрения наглядности следует представить распределение вероятностей в виде соответствующих масс на оси. Сумма всех масс равна единице. Аналогично центру тяжести масс в механике вводится понятие математического ожидания M (x). Пусть с экспериментом связаны события

x1, x2 , ..., xn и пусть P1, P2 , ..., Pn – вероятности этих событий.

Математическим ожиданием или средним значением вели-

чины называется сумма

v=1

представляющая собой взвешенное среднее значение величины х, причем весами служат вероятности Р0 в точках сосредоточения массы.

Если при непрерывной случайной величине х частота ее значений в интервале от х до (х + ∆х) приблизительно равна ω(x)∆x, а приближенное значение величины х в этом интервале

M (x) = ∑xiωi (x)∆xi ,

∆xi

где суммирование распространяется по всем интервалам ∆х, то в пределе при ∆х → 0 получим точную формулу для математического ожидания:

−∞

101

∞

Интеграл αv = ∫ xvω(x)dx называется первым, вторым,

−∞

третьим и т.д. моментом функции распределения в зависимо-

сти от значения v = 1, 2, 3, … Первый момент соответствует среднему и обозначается µ1. Интегралы

−∞

называются центральными моментами.

Средняя величина m является своего рода мерой «положения» переменной х, ее понятие эквивалентно центру тяжести масс, распределенных по оси пропорционально вероятности. Второй центральный момент µ2 дает представление о том, насколько далеко распределяются значения переменной относительно среднего значения. Это понятие аналогично центральному моменту инерции при указанном распределении массы. Второй момент называется случайной дисперсией случайной величины:

−∞

Принято в качестве характеристик рассеивания рассматривать величину той же размерности, что и сама случайная величина, которая называется стандартом или средним квадратичным отклонением, обозначается σ и принимается равной неотрицательному корню из µ2:

5.3. Корреляция. Коэффициент корреляции

При анализе различного рода нагрузок часто необходимо выяснить их зависимость от некоторых параметров. Для случайных величин вводится понятие корреляционной связи. Под

102

корреляционной связью понимают искомую связь случайных величин, когда каждому значению одной переменной соответствует вероятное значение другой переменной, относительно которого наблюденные значения могут быть распределены согласно какому-либо закону распределения вероятности. Чем ближе наблюденные значения к вероятному значению, тем более определенной является зависимость между переменными или, другими словами, тем сильнее корреляционная связь между ними.

Если обе переменные совершенно не зависят одна от другой, то корреляция между ними отсутствует. Корреляционная связь может быть как линейной, так и нелинейной и существовать между двумя, тремя и большим числом переменных.

Для определения уравнения корреляционной зависимости применяется метод наименьших квадратов.

Рассмотрим определение корреляционной зависимости для двух переменных х и у.

Связь предполагается линейной, определим ее в виде зависимости между ∆х и ∆у:

∆x = x −mx , ∆y = y −my ,

103

Откуда

и, следовательно,

= ∑n= ∆yi∆xi

a i 1 . (5.9)

∑in=1 ∆xi2

Близость экспериментальных точек к полученной зависи-

мости характеризуется коэффициентом корреляции

n

Максимальное значение ρ равно единице при σy = 0. Это

соответствует положению, когда все наблюденные точки лежат на прямой ∆y = a∆xi . Минимальное значение ρ равно 0, что со-

ответствует σy = σy . При ρ = 0 линейная корреляция отсутст-

вует. Однако может существовать какой-либо вид нелинейной корреляции.

104

Обычно для вычисления коэффициента корреляции пользуются другой зависимостью:

5.4.Случайные процессы

Впрактике исследований особенностей нагружения конструкции CДМ часто встречаются случайные величины, которые изменяются в зависимости от времени или какого-либо другого параметра, т.е. являются функцией этого параметра. Порывы воздуха в турбулентной атмосфере, нагрузки при движении по земле являются примерами таких функций.

Функция, значение которой при каждой данной величине независимой переменной является случайной величиной, на-

зывается случайной функцией.

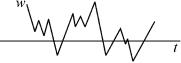
Случайная функция рассматривается как бесконечная совокупность случайных величин, зависящая от одной или нескольких непрерывно изменяющихся независимых переменных. В результате опыта случайная функция может при-

нимать конкретные формы, которые принято называть реализацией случайной функции или

возможным значением случайной функции, как, например, запись пульсаций турбулентности воздуха (рис. 5.5).

Можно представить, что сделано большое количество записей наблюдений в аналогичных условиях, которые образуют ансамбль событий. Пронумеруем эти записи: х1(t), х2(t), …,

хn(t).

Можно образовать следующее среднее статистическое первого, второго и т.д. порядка:

105

x2 (t), ... представляют собой средние по ансамблю случайного

процесса. Аналогично этому можно образовать средние параметры, показывающие внутреннюю связь случайного процесса по времени:

где τ – шаг выборки.

Эти средние называются средними по ансамблю корреляционных функций случайного процесса x(t).

Другим типом среднего является понятие среднего по времени. Для первого и второго порядка эти средние в интервале времени 2Т имеют вид:

чим через (x(t)) и (x 2 (t)). Если средние по времени при дос-

106

таточно больших f не зависят от t0 и T, то x(t) является стационарной функцией. Для стационарного случайного процесса функция распределения вероятности не зависит от смещения отсчета вдоль оси времени. При стационарном случайном процессе средние по времени будут равны средним по ансамблю, и поэтому нет необходимости для стационарного процесса различать средние по времени и средние по ансамблю.

В стационарности случайного процесса можно убедиться следующим образом. Предположим, что мы располагаем рядом записей случайного процесса. Если в результате обработки осциллограмм полученные средние x(t), x 2 (t) и x(t) x(t + τ) оказываются одними и теми же для любого момента времени t и любого фиксированного значения шага по времени τ, то процесс является стационарным. Если же средние зависят от момента времени t, для которого они определяются, то процесс является нестационарным.

Случайные функции, которые являются функцией времени, обычно называют случайными или стохастическими про-

цессами.

5.5. Корреляционная функция и ее свойства

Для стационарного случайного процесса x(t) корреляционная функция R(τ) может быть определена из соотношения

Физический смысл понятия корреляционной функции состоит в том, что она определяет некоторую осредненную связь между значениями случайной функции, находящимися на определенном расстоянии τ друг от друга, т.е. характеризует зависимую связь x(t) и х(t + τ). Если τ достаточно мало, то взаимная связь между значениями x(t) и х(t + τ) велика и отношение R(τ) / R(0) близко к единице. По мере увеличения τ взаимная

107

составляющая определяется начальными значениями x, связь между величинами x(t) и х(t + τ) ослабевает, они делаются взаимно независимыми, и функция R(τ) стремится к нулю. Таким

образом, при достаточно больших τ вероятность того, что величина х(t + τ) будет мало отличаться от величины x(t), практически равна нулю.

Корреляционная функция имеет следующие свойства:

1. Корреляционная функция R(τ) случайной функции со

средним значением m = 0 для достаточно больших τ стремится к нулю:

2. Начальное значение R(0) корреляционной функции R(τ) равно среднему значению квадрата случайной функции и поэтому существенно положительно:

3. Корреляционная функция R(τ) есть четная функция от τ:

Действительно,

R(τ) = x(t)x(t +τ) = x(t)x(t −τ) = R(−τ).

4. Значение корреляционной функции R(τ) в любом случае не превышает величины R(0), т.е. R(0) ≥ R(τ).

5.6. Спектральная плотность

Абсолютно интегрируемые функции f(t), т.е. функции, удовлетворяющие условию

108

∞

∫ f (t)dt < ∞,

−∞

могут быть представлены в виде интеграла Фурье:

Функция F(iω) называется преобразованием Фурье или

комплексным спектром функции f(t).

Рассмотрим стационарный случайный процесс х(t), для которого среднее значение m равно 0.

Усечем функцию х(t) таким образом, чтобы она была равна 0 вне интервала (–Т, Т), и обозначим усеченную функцию

хТ(t), т.е. хТ(t) ≠ 0 при –Т ≤ t ≤ Т, хТ(t) = 0 при прочих значениях t.

Определим понятие спектральной плотности S(ω) как преобразование Фурье от корреляционной функции R(τ):

Спектральная плотность обладает следующими свойствами:

1.Если R(τ) – монотонно убывающая функция от τ, то S(ω) также монотонно убывающая функция от ω.

2.Чем ýже функция R(τ), тем более пологой и широкой является функция S(ω). Если R(τ) стремится к нулю в течение

109

очень короткого промежутка времени ∆, то S(ω) сохраняет приблизительно постоянное значение до частоты порядка 2∆π.

Такого рода спектр S(ω) часто называют белым спектром. Предельный случай, когда S(ω) = const, соответствует отсутствию всякой корреляции между последующими значениями х(t).

5.7. Анализ действия динамических нагрузок на линейную систему

При динамическом действии внешней нагрузки значительное влияние на характер и величину усилий в элементах конструкции оказывают упругие колебания конструкции.

Приближенное решение задачи о действии динамических нагрузок на конструкцию можно получить двумя методами:

а) разделить всю конструкцию СДМ на n элементов, имеющих заданную массу mi, момент инерции Ji и соединенных между собой упругими связями определенной жесткости. В этом случае задача сводится к интегрированию системы 2n дифференциальных уравнений второго порядка, так как для каждого элемента можно составить два уравнения, одно из которых будет описывать поступательное движение i-го элемента, а другое – его поворот;

б) приняв в рассмотрение ограниченное число собственных форм колебаний конструкции, свести решение задачи к системе с конечным числом степеней свободы. При известных формах fi(z) вынужденные колебания конструкции можно представить системой уравнений вида

где Qi – нагрузка на i-й элемент; р – собственная частота системы.

110