
Прикладная теория колебаний
..pdfи заднего x2 мостов и расположенных над ними точек кузова.
Высоты неровностей под передними и задними колесами обозначим соответственно f1 и f2.
Такой выбор координат позволяет получить уравнения движения для передней и задней осей в одинаковой форме.
Введем следующие обозначения: m1, m2 – неподрессоренные массы переднего и заднего мостов; M, I – масса и момент инерции кузова относительно центральной оси, перпендикулярной к плоскости чертежа; cш, с, α – жесткости шин, подвесок и коэффициенты вязкого трения в амортизаторах (под с и α понимаются суммарные величины для левых и правых элементов подрессоривания); Р1, Р2 – силы взаимодействия подвесок с кузовом.
Получим следующие уравнения:
– для подвесок:
cшi ( fi − xi ) − Pi = mi xi ; |
|
|
|
|
||||||||||||
ci ( yi − xi ) +α( yi |
− xi ) = Pi |
|
|
(5.49) |
||||||||||||
|
|
|
|
|
(i = 1,2); |
|
|
|
|
|||||||
– движения кузова: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M |
|
y1 |
b |
+ y2 |
|
a |
|
= P1 + P2 ; |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
L |
|
L |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(5.50) |
||||
|
|
y1 − y2 |
|
|
|
|
|
|
|
|
|
|
||||
I |
|
|
= Pa − P b, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
L |
|
|
|
|
1 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где а и b – расстояния от центра тяжести (ц.т.) |
до переднего |
|||||||||||||||
и заднего мостов соответственно. |
|
|
|
|
|
|
|
|||||||||
Решим уравнения (5.50) относительно Р1 и Р2: |
||||||||||||||||
P = |
Mb2 + I |
y + |
Mab − I |
y |
; |
|
||||||||||
|
L2 |
|
|
|
L2 |
|
||||||||||
1 |
|
|
1 |
|
|
|
2 |
|
|
(5.51) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
Mab − I |
y + |
Ma2 + I |
y |
|
. |
|
|||||||||
|
|
L2 |
|
|
L2 |
|
|
|||||||||
2 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
121 |
Стр. 121 |
ЭБ ПНИПУ (elib.pstu.ru) |

Для современных компоновок грузовых автомобилей отношение
ε = |
I |
≈1. |
(5.52) |
|
Mab |
||||
|
|
|
Вэтом случае выражения (5.51) существенно упрощаются
ипринимают вид
P1 = M1 y1, |
P2 = M2 y2 , |
(5.53) |
|||||||
|
= M |
b |
|
= M |
a |
|
|||
M1 |
|
|
, M2 |
|
|
. |
|||
L |
L |
||||||||
|
|
|
|
|
|||||
Таким образом, при условии (5.52) колебания передней и задней частей автомобиля независимы. Именно этот простейший случай мы здесь и рассмотрим.
Для каждой из частей автомобиля, подставив значения P из (5.53) в (5.49), получим независимые уравнения (индексы 1, 2 опускаем):
Mi y +mx +cшx = cш f ; |
|
(5.54) |
||||
Mi y +cy +αy −cx −αx = 0. |
|
|||||
|
|
|||||
Подставив в (5.54) |
|
= f |
eiωt ; |
x = x eiωt ; |
y = y eiωt |
и ис- |
f |
||||||
0 |
|
0 |
0 |
|
||
ключив x, находим комплексную частотную характеристику для вертикального перемещения кузова:
F(iω) = |
|
y |
|
= |
|
|
|
|
|
|
|
||
f |
|
|
||||
|
|
|
|
|
||
4 |
+с) |
|
2 |
|||
= cш(с+iαω) {Mimω − Mi (cш |
+ mc |
ω +cшc − |
||||
−iα ω3 (Mi +m) |
−ωcш }. |
(5.55) |
||||
Далее, зная спектральную функцию неровностей Sf (ω), можно вычислить и спектральную функцию перемещений:
Sy (ω) = |
|
F(iω) |
|
2 S f (ω). |
(5.56) |
|
|
122
Стр. 122 |
ЭБ ПНИПУ (elib.pstu.ru) |

Разумеется, спектральная функция неровностей дороги, полученная по экспериментальной корреляционной функции kf (z), задается не в зависимости от ω, а в функции пространственной частоты Ω (1/м):
1 ∞
S0 (Ω) = 2π ∫0 k(z)cos Ωzdz.
Как нетрудно установить, при движении со скоростью v
(м/с) Ω = ωv . Поэтому
S f |
(ω) = |
1 |
S0 |
|
ω |
(5.57) |
v |
|
. |
||||
|
|
|
|
v |
|
Таким образом, переход от пространственной спектральной функции к временной сводится к изменению масштабов по координатным осям. С увеличением скорости движения график S f (ω) растягивается по горизонтали и сокращается по
вертикали (при этом площадь под кривой S f , равная дисперсии Df , остается постоянной).
Статистические характеристики смещения кузова y не представляют существенного интереса. Комфортабельность авто-
мобиля в значительной степени зависит от ускорений j = |
d 2 y |
. |
||
dt |
2 |
|||
|
|
|||
Легко видеть, что для этой величины комплексная передаточная функция определяется выражением
F (iω) = −ω2 F(iω). |
(5.58) |
i |
|
Рассмотрим пример – колебания передней части шасси автокрана при движении по асфальтобетонной дороге. Подвеска характеризуется следующими данными:
М= 82 кг·с2/м (800 кг); m = 10,2 кг·с2/м (100 кг);
с= 50 кг/см (51 · 103 Н/м); сш = 330 кг/см (336 · 103 Н/м);
123
Стр. 123 |
ЭБ ПНИПУ (elib.pstu.ru) |

α = 3,2 кг·с/см (3,26 · 103 Н·с/м).
Примем, что корреляционная функция дороги выражается формулой
k(z) = Df e−γ z ,
где Df = 2,0 см2; γ = 0,133 1/м.
Этой функции соответствует пространственная спектральная функция
S0 (Ω) = π2 Df γ2 +γΩ2 .
Соответственно при движении со скоростью v временная спектральная функция
S f |
(ω) = |
1 |
S0 |
|
ω |
= |
2 |
Df |
|
γ1 |
, |
|
|
|
|
|
|
||||||
v |
π |
2 |
2 |
||||||||
|
|
|
|
v |
|
|
γ1 |
+ω |
|
где γ1 = γv.
Проведем расчет при скорости v = 15 м/с (54 км/ч). В этом случае γ1 = γv = 2,0 c−1.
Находим спектральную функцию ускорения кузова:
S j (ω) = S f (ω) Fj (iω) 2 = ω4S f (ω) F(iω) 2 .
Подстановка значений приводит к формуле
S j (ω) = |
2 |
|
|
|
|
|
γ1 |
|
|
cш2 |
|
(c2 +α2ω2 )ω4 |
|
|
|
|
|||||||||||||
|
|
Df |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
, |
|
|
|
|
|||||
π |
|
2 |
2 |
M |
2 |
m |
2 |
|
|
Φ(ω) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
γ1 |
+ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
c |
|
|
c |
|
|
c c |
|
|
α |
|
|
|
|
M |
|
c |
||||||||||
Φ(ω) = ω4 −ω2 |
|
|
ш |
|
+ |
|
|
+ |
|
|
+ |
|
ш |
|
|
+i |
|
ω3 |
1 |
+ |
|
|
−ω |
ш |
. |
||||
|
|
m |
|
mM |
|
m |
|
||||||||||||||||||||||
|
|
m |
|
M |
|
|
|
|
M |
|
|
|
|
|
|
m |
|||||||||||||
Спектральная функция Sj ускорения имеет вид, представленный на рис. 5.14.
124
Стр. 124 |
ЭБ ПНИПУ (elib.pstu.ru) |
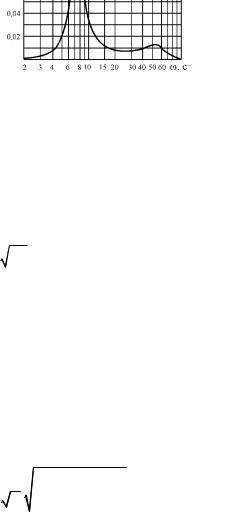
Дисперсия ускорения определяется интегралом
∞
Dj = ∫ S j (ω)dω.
0
Интеграл такого типа может быть вычислен аналитически, но более быстро ведет к цели численное интегрирование.
Таким образом, в данной
задаче получено значение Dj = = 1,05 (м/с2)2.
Рис. 5.14. Спектральная функция ускорения
Следовательно, среднеквадратическое ускорение
σj = Dj =1,02 м/с2.
Для оценки этой величины отметим, что максимальное
ускорение туловища человека при нормальной ходьбе составляет ±2,5 м/с2.
5.9. Расчет на ограниченную долговечность
Коэффициент запаса прочности из условия ограниченной долговечности при непрерывном законе распределения напряжений определяется следующим образом:
η= |
σ2D = |
|
|
|
σ2D |
|
|
|
, |
(5.59) |
||
|
|
|
|
|
|
|
||||||
|
σпр 1 |
m |
N j |
|
∑ |
|
σam |
nj |
|
|||
|
|
m d |
N0 |
|
j=1 |
N j |
|
|
||||
|
|
|
|
|
|
|
||||||
где σ2D – предел выносливости конструкции (образца) при ба-
зовом числе испытаний; N0 – база испытаний на кривой усталости, для сталей N0 = 107 циклов, для алюминиево-магниевых сплавов N0 = (2÷5) · 107 циклов; d – коэффициент, характери-
125
Стр. 125 |
ЭБ ПНИПУ (elib.pstu.ru) |
зующий свойства материала, режим нагружения и склонность к образованию микротрещин (как правило, d = 0,3÷0,5); m – показатель кривой усталости, равный котангенсу угла наклона левой ветви кривой, на основе экспериментальных данных можно принять m = 4÷6; σа – амплитуда циклов переменных напряжений, возникающих в корпусе и превышающих минимальные (σmin); Nj – среднее количество циклов напряжений σа, превышающих фиксированный уровень напряжений (σmin), за время эксплуатации в рассматриваемом режиме; f(σа) – функция плотности распределения амплитуд переменных напряже-
ний σа.
Исследования в автомобильной промышленности показали, что определенное влияние на долговечность конструкции оказывает напряжение ниже предела выносливости, поэтому в качестве нижнего фиксированного уровня напряжений принимают
σmin = 0,8σ2D .
Среднее число амплитуд напряжений в диапазоне
σmin = 0,8σ2D ÷σmax = 3 σ2
за период эксплуатации в рассматриваемом режиме определяется зависимостью, полученной на основе формулы Раиса:
σmax |
L |
σ |
|
|
|
|
σ |
|
|
|
2 |
|
|
|
2 |
||
nj ∑ |
2π σ |
σ2 |
exp |
− |
|
ai |
||
σmin |
|
|
|
2 σ2 |
||||
|
|
|
|
|
|
|
|
|
σ2
− − ai
2
exp
+∆D |
|
|
|
, (5.60) |
|
i |
||
σ2 |
|
|
|
|
|
где σ – скорость изменения величины σ,
|
1 |
ω |
|
1 |
ω |
σ2 = |
∫0 Sσ(ω)dω, |
σ2 = |
∫0 Sσ(ω)dω, |
||
|
π |
0 |
|
π |
0 |
|
|
|
|
Sσ(ω) = ω2Sσ(ω).
126
Стр. 126 |
ЭБ ПНИПУ (elib.pstu.ru) |
6.ВИБРОДИАГНОСТИКА
6.1.Виброакустические диагностические параметры
Вибрации, формируемые механизмами и сопряжениями двигателя внутреннего сгорания, можно рассмотреть как случайный процесс, который оценивается плотностью распределения, математическим ожиданием, корреляционной функцией, спектральной плотностью и другими статистическими характеристиками.
Виброакустические параметры ДВС подчиняются нормальному закону распределения (закону Гаусса):
f (X ) = σ |
|
|
− |
( X −M ( X ))2 |
|
|
|
2π e |
|
, |
(6.1) |
||||
|
|
1 |
|
|
2σ2 |
|
|
где М(Х) – математическое ожидание (центр рассеивания); σ – среднее квадратичное отклонение величины X; σ2 – дисперсия.
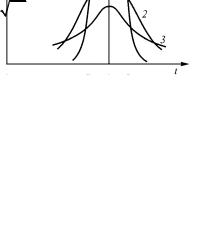
Наибольшая |
ордината |
|
|
кривой распределения обрат- |
|
||
но пропорциональна σ, при |
|
||
увеличении σ максимальная |
|
||
ордината уменьшается. По- |
|
||
скольку площадь кривой рас- |
|
||
пределения равна единице, то |
|
||
при увеличении σ кривая рас- |
|
||
пределения становится более |
|
||
плоской. |
Для |
нормального |
Рис. 6.1. Кривые нормального за- |
закона распределения разброс |
кона распределения: 1 – парамет- |
||
значений укладывается в диа- |
ры виброимпульса, выделенные по |
||
пазон М(Х) ± 3σ. |
|
частоте и времени; 2 – уровень |
|
На |
рис. 6.1 приведены |
вибрации в активной полосе час- |
|
кривые |
распределения диаг- |
тот; 3 – общий уровень вибраций |
|
в области проверяемого сопря- |
|||
ностических параметров. Вы- |
жения |
||
|
|
|
127 |
Стр. 127 |
ЭБ ПНИПУ (elib.pstu.ru) |
деление диагностического сигнала, выбор оптимальных зон для установки датчиков, благоприятного режима работы двигателя способствуют уменьшению рассеивания диагностических параметров.
Одним из наиболее простых виброакустических параметров является общий уровень вибрации, регистрируемый в диагностических дефектационных зонах блока и механизмов двигателя. Для диагностики механизмов и сопряжений по общему уровню вибрации необходимо знать математическое ожидание общего уровня для начального и предельно изношенного состояний.
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины Хi (в нашем случае общий уровень вибрации в диагностической зоне механизма по множеству двигателей данной марки) и вероятностей Рi этих значений:
n |
|
M (X ) = ∑ Xi Pi . |
(6.2) |
i=1
Кроме того, математическое ожидание случайной величины – это среднее арифметическое наблюдение значений случайной величины:
M (X ) = |
∑n |
Xi |
|
|
i=1 |
|
, |
(6.3) |
|
n |
|
|||
|
|
|
|
где Xi – значение случайной величины в i-м двигателе; п – число двигателей или однотипных механизмов.
При увеличении числа опытов с большим количеством однотипных механизмов по начальным и предельным состояниям статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. Так, исследования 40 цилиндров тракторных двигателей СМД-14, поступивших на капитальный ремонт и вышедших из ремонта, показали, что среднее статистическое по общему уровню вибрации в области цилиндров для отремонтированных двигателей (с зазорами
128
Стр. 128 |
ЭБ ПНИПУ (elib.pstu.ru) |
в сопряжениях поршень – гильза s = 0,18…0,22 мм) составляет 5g, а для предельно изношенных (с зазорами s = 0,6…0,64 мм) – 20g. Зная среднее статистическое по множеству, можно определить состояние цилиндров двигателя по общему уровню вибрации.
6.2. Частотное выделение виброакустического диагностического сигнала
При исследовании колебательных процессов пьезоэлектрический датчик ускорений преобразует механические колебания деталей в электрический сигнал, т.е. X (t) = AI (t), где
А – коэффициент преобразования. Специальной электронной виброакустической аппаратурой сложное колебание тока I(t) разлагается на составляющие пропорционально измеряемому параметру X(t).
Сложное колебание может быть представлено в виде бесконечного числа гармонических составляющих:
∞ |
|
X (t) = C0 ∑Ck cos(kω0t −ϕk ), |
(6.4) |
k=1
где С0 – амплитуда центральной частоты; Сk – составляющая выделенной полосы частот,
|
|
1 |
T / 2 |
X (t)e− j 2πn |
t |
||
Ck |
= |
∫ |
|
dt; |
|||
T |
|||||||
T |
|||||||
|
|
|
|
|
|||
|
|
|
–T / 2 |
|
|
|
|
ϕk – фазовый угол.
Ряд Фурье (6.4) представляет периодическую функцию как сумму периодических составляющих и применяется для разложения периодических функций с линейчатым спектром. Это разложение можно применить и для случая непериодической функции, имеющей сплошной спектр. При рассмотрении непериодической функции интеграл Фурье может быть получен как предельный случай периодической функции при периоде Т → ∞.
129
Стр. 129 |
ЭБ ПНИПУ (elib.pstu.ru) |
Выражение для непериодической функции примет вид
|
∞ |
|
||
X (t) = ∫ X (t)cos(ωt)dt, |
|
|||
|
−∞ |
|
||
или |
|
|||
|
1 |
∞ |
|
|
X (t) = |
∫ ST (ω)e jωt dt, |
(6.5) |
||
2π |
||||
|
|
−∞ |
|
|
где ST(ω) – функция, которая характеризует спектральную плотность и выражает характер изменения амплитуд по частоте.
Из выражения (6.5) определяется спектральная плотность амплитуд
∞ |
|
ST (t) = ∫ X (t)e− jωt dt. |
(6.6) |
−∞
Формула (6.6) позволяет непериодические функции представить суммой периодических составляющих.
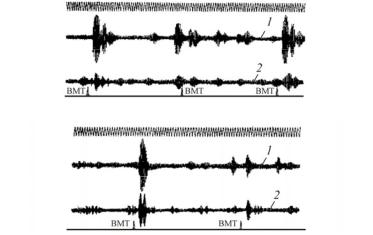
Осциллограммы (рис. 6.2) временных реализаций вибраций гильзы и блока, на которых записаны колебания выделенных
а
б
Рис. 6.2. Осциллограммы, снятые на работающем двигателе СМД-14А: а – вибрации на выделенной частоте 1 кГц; б – на частоте 2,8 кГц; 1 – ускорение вибрации гильзы; 2 – ускорение вибрации блока
130
Стр. 130 |
ЭБ ПНИПУ (elib.pstu.ru) |
