Вероятностные методы расчета конструкций

Однако применение гармонического анализа непосредственно к случайным процессам неприемлемо, так как стационарный случайный процесс не затухает во времени и не удовлетворяет некоторым условиям, необходимым для представления его интегралом Фурье. Но так как характеристики случайного процесса детерминированны, то к ним применима теория интегралов Фурье.

Впервые А.Я. Хинчиным было доказано, что любой стационарный случайный процесс можно рассматривать как наложение некоррелированных друг с другом гармонических колебаний различных частот со случайными фазами и амплитудами.

К понятию о спектре случайной функции можно подойти из следующих соображений. Рассмотрим стационарную центрированную случайную функцию X (t) на интервале (0, T). Учи-

тывая, что корреляционная функция рассматриваемой функции четная, ее можно разложить на интервале (–T, T), используя только четные гармоники, т.е.

Kx (t1,t2 ) (Di cos it1 cos it2 Di sin it1 sin it2 ). (2.26)

i 0

Но выражение (2.26) есть не что иное, как каноническое разложение корреляционной функции, координатными функциями которого являются косинусы и синусы частот, кратных1. Зная каноническое разложение корреляционной функции,

61

можно построить каноническое разложение самой случайной функции с теми же координатными функциями и с дисперсиями, равными коэффициентам Di в каноническом разложении

корреляционной функции:

X (t) (Ui cos it1 cos it2 Vi sin it1 sin it2 ), (2.27)

i 0

где Ui ,Vi – некоррелированные центрированные случайные величины, для которых

D(Ui ) D(Vi ) Di .

Разложение (2.27) называется спектральным разложением стационарной случайной функции (изображает стационарную случайную функцию, разложенную на гармонические колебания различных частот, причем амплитуды этих колебаний являются случайными величинами). Дисперсия случайной функции (2.27)

Таким образом, дисперсия стационарной случайной функции равна сумме дисперсий всех ее гармоник спектрального разложения, т.е. дисперсия Dx известным образом распределена

по разным частотам: одним частотам соответствуют большие дисперсии, другим – меньшие. Распределение по частотам можно проиллюстрировать графически в виде так называемого спектра дисперсий (рис. 2.6, а), представляющего собой ряд отдельных дискретных линий, разделенных равными промежут-

ками ( 1 T ) . Сумма всех ординат построенного спектра

равна дисперсии случайной величины.

Наши знания о случайной функции будут тем полнее, чем больший участок времени мы будем рассматривать, поэтому перейдем в разложении к пределу T . В этом случае рас-

62

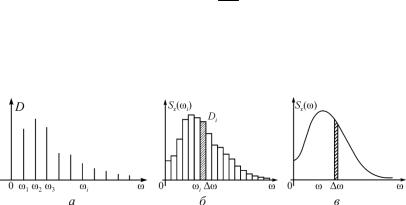
стояние между частотами будет неограниченно уменьшаться, а дискретный спектр будет приближаться к непрерывному (рис. 2.6, б). При построении этого графика будем откладывать по оси ординат не саму дисперсию Di , а среднюю плотность

дисперсии, т.е. дисперсию, приходящуюся на единицу длины данного интервала частот (на каждом отрезке , как на основании, строим прямоугольник с площадью Di ). Получаем сту-

пенчатую диаграмму. Высота прямоугольника на участке , прилежащем к точке i ,

D

Sx ( i ) i

и представляет собой среднюю плотность дисперсии на этом участке. Суммарная площадь всей диаграммы, очевидно, равна дисперсии случайной функции.

Рис. 2.6

При неограниченном увеличении интервала ступенчатая кривая будет неограниченно приближаться к плавной кривой Sx ( ) (рис. 2.6, в). Эта кривая изображает плотность распреде-

ления дисперсии по частотам непрерывного спектра, а сама функция Sx ( ) называется спектральной плотностью дисперсии

или спектральной плотностью стационарной центрированной случайной функции X (t) . Очевидно, площадь, ограниченная

кривой Sx ( ) , по-прежнему должна равняться дисперсии Dx случайной функции X (t) :

63

Формула (2.28) есть не что иное, как разложение дисперсии Dx на сумму элементарных слагаемых Sx ( )d .

Таким образом, мы ввели в рассмотрение новую дополнительную характеристику стационарного случайного процесса – спектральную плотность, описывающую частотный состав стационарного процесса. Однако эта характеристика не является самостоятельной; она полностью определяется корреляционной функцией данного процесса. Подобно тому, как ординаты дискретного спектра Di выражаются формулой (2.25) через корре-

ляционную функцию Kx ( ) , спектральная плотность Sx ( ) также может быть выражена через корреляционную функцию:

Sx ( ) 2 Kx ( )cos d . (2.29)

0

В ряде случаев с точки зрения простоты математических преобразований оказывается удобным пользоваться не действительной, а комплексной формой записи как спектрального разложения случайной функции, так и ее характеристик: спектральной плотности и корреляционной функции. Комплексная форма записи удобна, в частности, потому, что всевозможные линейные операции над функциями, имеющими вид гармонических колебаний (дифференцирование, интегрирование, решение линейных дифференциальных уравнений и т.д.), осуществляются гораздо проще, когда эти гармонические колебания записаны не в виде синусов и косинусов, а в комплексной форме, в виде показательных функций. Комплексная форма записи корреляционной функции и спектральной плотности применяется

ив тех случаях, когда сама случайная функция (а следовательно,

иее корреляционная функция и спектральная плотность) действительна.

64

Корреляционная функция стационарного эргодического случайного процесса в комплексном виде может быть представлена интегралом Фурье:

где Sx( ) – неслучайная функция (спектральная плотность случайного процесса X(t)).

Выполняя обратное преобразование, будем иметь:

Используя эти соотношения, можно установить важную зависимость между дисперсией и спектральной плотностью:

Формулы (2.29) и (2.30) называются формулами Винера – Хинчина.

Покажем, как можно вычислять спектральные плотности производных стационарных функций. Подставляя в формулы (2.11) соотношение (2.29), получим:

65

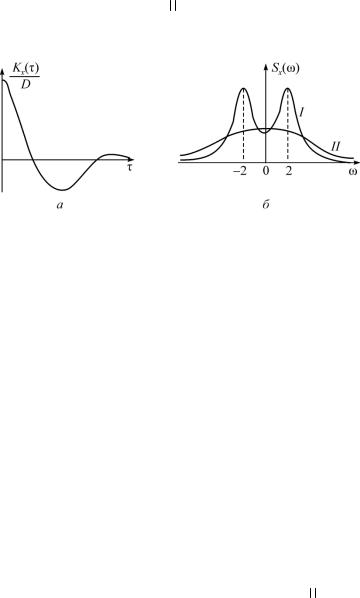
Пример 2.6. Корреляционная функция случайной функции X (t) имеет вид: Kx ( ) De cos (рис. 2.7, а). Определить спектральную плотность Sx ( ).

Рис. 2.7

Решение. Представляем Kx ( ) в комплексной форме:

Спектральную плотность Sx ( ) находим поформуле (2.31):

Отсюда после элементарных преобразований получаем:

Вид графика спектральной плотности (рис. 2.7, б) зависит от соотношения параметров и , т.е. от того, что преобладает

в корреляционной функции: убывание по закону e или коле-

66

бание по закону cos . Очевидно, при сравнительно малых

преобладает колебание, при сравнительно больших – убывание. В первом случае случайная функция близка к периодическим колебаниям частоты со случайной амплитудой и фазой;

соответственно, в спектре случайной функции преобладают частоты, близкие к частоте . Во втором случае спектральный со-

став случайной функции более равномерен, преобладания тех или иных частот не наблюдается; в пределе при спектр случайной функции приближается к спектру белого шума.

В качестве иллюстрации на рис. 2.7, б изображены спектральные плотности для следующих случаев: 1) 2, 1

(кривая I); 2) 2, 3 (кривая II). Как видно из чертежа, при

1 спектр случайной функции обнаруживает ярко выраженный максимум в области частот . При 3 (кривая II)

спектральная плотность в значительном диапазоне частот остается почти постоянной.

В прил. 2 приведены виды случайных функций и соответствующих им корреляционных и спектральных функций,

ав прил. 3 их математическое описание.

Врамках приведенных определений можно привести решение задачи надежности (задача о выбросах) и задачи о свободных линейных колебаниях систем.

2.5. Марковские процессы

Корреляционная теория позволяет провести анализ систем с линейной связью между входом и выходом. В этом случае корреляционная теория дает возможность получить вероятностные характеристики решения дифференциальных уравнений, если известны вероятностные характеристики возмущений. Однако получить решение нелинейных уравнений на основе корреляционной теории нельзя. Не всегда удается решить и задачу об определении вероятности превышения ординатой случайной функции заданных значений. Во всех этих случаях могут быть полезны

67

марковские процессы, для полной характеристики которых достаточно знать только двумерные законы распределения.

Случайный процесс называется марковским, если распределение в момент времени t2 может быть выражено через распределение в предшествующий момент времени t1 < t2 независимо от предшествующей истории процесса. Таким образом, марковский процесс – это процесс без последействия. Марковские процессы являются абстракцией реальных процессов. Однако многие реальные процессы могут приближенно трактоваться как марковские или, во всяком случае, могут рассматриваться как компоненты многомерных марковских процессов.

Выделение марковских процессов в отдельный класс вызвано рядом причин, важнейшими из которых являются относительная простота случайного процесса, описывающего эволюцию системы, наличие возможности использовать хорошо разработанный математический аппарат для аналитического исследования марковских процессов, возможность получения аналитических выражений для показателей качества систем и, наконец, возможность сведения к указанным процессам более общих процессов.

где f (xn x0 , x1,..., xn 1 ) – условная плотность вероятности xn при условии, что в предыдущие моменты времени процесс x(t) характеризовался значениями x0 , x1,..., xn 1.

68

Процесс называется марковским, если

т.е. если значение случайного процесса в некоторый момент времени зависит только от предыдущего значения.

Тогда многомерная плотность распределения

Для марковского процесса любые многомерные распределения могут быть выражены через условные двумерные. Функ-

цию f (xi ,ti xi 1,ti 1 ) , равную условной плотности вероятности перехода из состояния xi 1 в состояние xi , называют еще пере-

ходной плотностью вероятности. Можно получить интегральное, а затем дифференциальное уравнение, которому должна удовлетворять переходная плотность вероятности.

Ранее (см. (1.9)) было показано, что одномерную плотность вероятности можно получить через двумерную. Тогда, рассматривая три последовательных момента времени: t0 t1 t2 , мож-

но записать:

f (x2 ,t2 , x0 ,t0 ) f (x2 ,t2 , x1,t1, x0 ,t0 )dx1.

Согласно соотношению (2.37) будем иметь:

f (x2 ,t2 x0 ,t0 ) f (x0 ,t0 )

f (x2 ,t2 x1 ,t1 ) f (x1,t1 x0 ,t0 ) f (x0 ,t0 )dx1

или

f (x2 ,t2 x0 ,t0 ) f (x2 ,t2 x1 ,t1 ) f (x1,t1 x0 ,t0 )dx1. (2.38)

69

Уравнение (2.38) в математической литературе называют уравнением Чепмена – Колмогорова, в литературе по физике – уравнением Смолуховского, который получил его при исследовании броуновского движения частицы. Уравнение (2.37) накладывает весьма жесткие ограничения на вид условной плотности вероятности перехода, а именно: интегрирование по х1 должно привести к исключению х1, причем вид функции f должен ос-

таться неизменным. Пределы интегрирования не обязательно должны быть равны бесконечности.

Получим дифференциальное уравнение, которому должна удовлетворять условная плотность вероятности перехода. В дальнейшем будем рассматривать непрерывный случайный процесс (процесс х(t) считается непрерывным, если за малые промежутки времени t функция х(t) может получить заметные по величине приращения лишь с малой вероятностью).

Далее в уравнении (2.38) заменим: t1 = t0 + t ( t > 0) и t2 = t, получим:

по х1 в окрестности точки х0 (ограничившись первыми тремя членами разложения):

70