Вероятностные методы расчета конструкций

Пример 6.1 [4]. Объект массой т связан с основанием пружиной жесткостью с и демпфером вязкого трения (коэффициент вязкого трения α) (рис. 6.2). Предположим, что случайная нагрузка q(t) соответствует ограниченному белому шуму в диа-

Уравнение движения массы

191

При 0 0

при 0 Sx ( ) 0.

Для спектральной функции скорости и ускорения получаем:

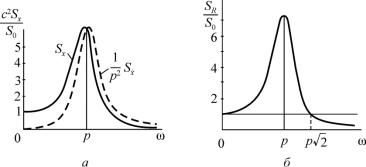
На рис. 6.3 приведены графики Sx , Sx , SR для значения коэффициента затухания n / p 0,2 в предположении p .

Рис. 6.3

Как видно из этих графиков, при постоянной плотности воздействия спектр колебаний неравномерен. Система усиливает колебания с частотами, близкими к собственной частоте, и ослабляет высокочастотные колебания.

192

Определение дисперсии всех определяемых величин сводится к вычислению интегралов. В частности, дисперсия перемещения

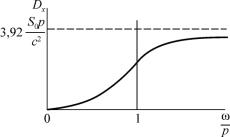
Эти интегралы табулированы [20]. На рис. 6.4 показана зависимость дисперсии перемещения от относительной частоты внешней нагрузки при n / p 0,2 .

Из графика следует, что дисперсия возрастает главным образом за счет колебаний с частотами, близкими к собственной частоте системы. При неограниченном спектре возмущения ( 0 ) дис-

При 0 дисперсия силы, передаваемой основанию,

Из полученного выражения следует, что дисперсия неограниченно возрастает при n 0 (при этом возрастает амплитуда колебаний вблизи резонансной частоты) и при n (непосредственная передача возмущающей силы на основание). Минимальное значение дисперсия принимает при n p / 2 (при

этом декремент затухания 3,64):

193

DRmin S0 p.

Отметим ряд трудностей, сопутствующих приведенному решению:

1. При случайном возбуждении типа белого шума наивыгоднейшим является весьма большое демпфирование системы. Как и при расчете системы виброизоляции, при синусоидальном возбуждении выясняется, что система тем более эффективна, чем ниже частота ее настройки p . Но это означает, что жест-

кость соединения объекта с основанием должна быть минимальна, а это в свою очередь ведет к недопустимо большим перемещениям объекта. Это затруднение можно преодолеть, дополняя условие минимума критерия качества ограничениями, которые накладываются на параметры.

2.В зависимости от того, что минимизируется – средний квадрат ускорения или средний квадрат относительного перемещения, получаются различные решения.

3.Оптимальные параметры линейной виброзащитной системы зависят от интенсивности воздействия. В реальных конструкциях интенсивность вибрационного воздействия редко остается постоянной в течение срока эксплуатации конструкции. Линейные системы, параметры которых подобраны применительно к некоторому уровню воздействия, перестают быть оптимальными при изменении этого уровня. Для выхода из создавшегося затруднительного положения приходится интерпретировать линейную систему как результат статистической линеаризации некоторой нелинейной системы. Эти трудности усугубляются, если объект обладает несколькими степенями свободы и если внешнее воздействие является нестационарным случайным процессом.

Трудности преодолеваются выбором более удачного критерия качества для виброзащитной системы, ибо основным требованием к ней является требование надежного функционирования. Конечно, средние квадраты перемещений и ускорений объекта в некоторой степени характеризуют условия надежного

194

функционирования. Но с технической точки зрения было бы правильнее минимизировать вероятность того, что за время эксплуатации объекта его параметры хотя бы раз выйдут из области допустимых значений.

Таким образом, оптимизация по надежности, будучи более естественной и обоснованной, в то же время снимает трудности, возникающие при применении более частных критериев. Этот метод оптимизации применим как к линейным, так и к нелинейным системам с произвольным числом степеней свободы, кроме того он не накладывает дополнительных ограничений на стохастическую природу внешних воздействий.

Общая постановка задачи о проектировании виброзащиты формулируется следующим образом [6]. Пусть некоторая механическая система с конечным или бесконечным числом степеней свободы прикрепляется к основанию при помощи конечного числа опор. В общем случае свойства этих опор неизвестны; тогда говорят о выборе структуры виброзащиты. Однако чаще система виброзащиты ищется в классе простых линейных связей, содержащих упругость и вязкое трение. В этом случае неизвестными параметрами являются координаты опор, коэффициенты их жесткости и вязкости. Под действием внешних сил или ускорений, сообщаемых основанию, в системе возникает некоторое вибрационное поле. Из технических соображений выбирается система параметров качества и допустимая область в пространстве параметров качества. Далее вычисляется показатель надежности системы как функция неизвестных параметров виброзащиты. Последние находятся из условия, чтобы этот показатель принимал максимальное значение. Как правило, показатели надежности как функции параметров виброзащиты не имеют изолированного максимума. Кроме того, указанные параметры обычно могут принимать значения лишь из некоторой ограниченной области. Поэтому проектирование виброзащиты сводится к неклассической задаче оптимизации, которая может быть разрешена лишь численными методами.

195

Одним из центральных остается вопрос о выборе параметров качества и области их допустимых значений. Наряду с ограничениями, накладываемыми на абсолютные ускорения, могут быть также поставлены ограничения на относительные перемещения различных точек системы.

Поясним постановку и метод решения задачи на следующем примере, в котором, как и в примере 6.1, рассмотрена одномассовая система, но колебания возникают за счет кинематического воздействия.

Пример 6.2 [6]. Пусть объект массой m при помощи упругой связи с жесткостью с и вязкой связи с коэффициентом трения α прикреплен к основанию, которое совершает случайные колебания по закону x0 (t) . Для надежного функционирования объекта требу-

ется, чтобы относительное перемещение и абсолютное ускорение объекта не превышали по модулю предельно допустимых значений. Требуется подобрать параметры оптимальной по надежности виброзащиты так, чтобы вероятность пребывания в допустимой области завремя 0 t T была максимальной.

Решение. Уравнение движения массы

196

Обозначим предельно допустимые значения относительного перемещения массы через u* , а абсолютного ускорения a x0 (t) u (t) через a* . Тогда ограничения в задаче, опреде-

ляющие область допустимых значений, можно записать в следующем виде:

В дальнейшем ограничимся случаем, когда ускорение основания x0 (t) представляет собой стационарный гауссовский

процесс. Тогда математическое ожидание числа выбросов из допустимой области (в нашем случае она двумерна) в единицу времени не будет зависеть от времени. Вместо критерия максимизации вероятности пребывания системы в допустимой области в этом случае может быть принят критерий минимума числа выбросов в единицу времени, т.е.

Поскольку допустимая область (6.13) представляет собой прямоугольник, то математическое ожидание числа выбросов

N (u* , a* ) находится по формуле:

N(u* , a* )

197

где 12 , 22 ,r – дисперсии и коэффициент корреляции процессов u(t) и a(t) соответственно; 12 , 22 – дисперсии процессов u(t) и a(t) .

Представим процесс x0 (t) в виде:

x0 (t) mx0 A(t)ei t ,

где A(t) – обобщенная случайная функция (спектр процесса). Представляя в аналогичной форме процесс u(t) :

Используя соотношения (6.16) и (6.17), применим формулу (6.15) для математического ожидания числа выбросов. Минимизация этой характеристики по варьируемым параметрам системы дает (при заданных ограничениях) решение задачи об оптимальной виброзащите.

На рис. 6.6 представлены некоторые численные результаты решения задачи 6.2 [6]. Ускорение x0 (t) выражено экс-

198

поненциально-коррелированным процессом, спектральная плотность которого

10 4 0 .

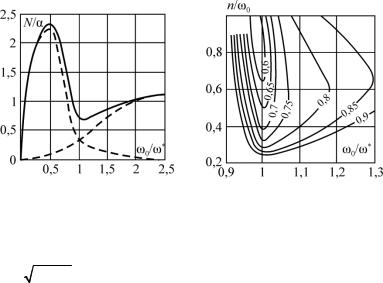
Рис. 6.6 Рис. 6.7

Сплошная линия на рис. 6.6 показывает зависимость отношения N / от безразмерной собственной частоты 0 / *

( * a* / u* ). Как видно из рис. 6.6, абсолютный минимум среднего числа выбросов соответствует собственной частоте0 , стремящейся к нулю. Однако из-за ограничений этот минимум не представляет интереса. Относительный минимум наблюдается вблизи частоты * . Штриховые линии на рис. 6.6

цисса точки пересечения этих линий близка к абсциссе относительного минимума числа выбросов из допустимой области (см. (6.13)). Этот факт становится понятным, если рассмотреть узкополосные колебания массы m. Для этих колебаний можно

принять, что a x0 02u.

199

Если * , то фазовая точка (u, a) будет двигаться по

траекториям, близким к диагонали прямоугольника области допустимых значений, определенной условиями (6.13). Минимум числа выбросов из этого прямоугольника достигается, таким образом, при условиях, обеспечивающих приблизительную рав-

ноопасность выбросов из полос u(t) u* и a(t) a*.

Зависимость математического ожидания числа выбросов от двух варьируемых параметров (безразмерной собственной частоты

0 / * и безразмерного параметра демпфирования n / 0 ) представлена на рис. 6.7. Вычисления выполнены при a* 0 и u* 2 10 4 0 . Кривые на этом графике соответствуют изолиниям равных значений N (u* ,a* ). Изменение демпфирования в ши-

роких пределах относительно мало влияет на число выбросов. Зависимостьэтого числаотсобственнойчастотыболее существенна.

Приведенные выше данные относились к случаю, когда вибрация основания представляет собой широкополосный процесс. По аналогии можно рассмотреть и узкополосный процесс. Расположение экстремумов существенно зависит от величины несущей частоты. При этом максимум соответствует резонансу системы с несущей частотой; минимумы, если они существуют, располагаются в дорезонансной области.

6.2. Оптимизация при вероятностных прочностных расчетах элементов конструкций

Проектирование различных конструкций требует компромиссного выбора ряда параметров. К их числу относятся параметры надежности технического устройства, форма и физические особенности его элементов, стоимость изготовления и затраты при эксплуатации. Надежность зависит от соотношения между распределениями случайных величин, которыми являются прочность S и напряжение (нагрузка) R. Параметры этих распределений (математические ожидания mR и mS и среднеквадра-

200