Вероятностные методы расчета конструкций

Решение обратной задачи может существенно осложниться, если имеется несколько входных воздействий (рис. В.2) и если требуется по поведению системы установить вероятностные характеристики каждого воздействия в отдельности.

Третья задача заключается в определении свойств стохастической системы по известным характеристикам на входе и выходе системы. В самом общем случае может оказаться неизвестной сама структура системы. Изучение свойств неизвестной системы путем сопоставления ее реакций с входным воздействием составляет так называемую проблему черного ящика. Однако так задача ставится весьма редко. Обычно же структура известна и даже известны некоторые сведения о ее свойствах, но в детерминированном виде. Тогда целью исследования является получение информации о стохастических свойствах системы. Сложности возникают, если внешнее воздействие сопровождается случайными помехами с неизвестными свойствами. Тогда, по существу, необходимо объединение второй и третьей задач.

Четвертая задача состоит в отыскании системы, которая при заданных внешних воздействиях обладает заданными свойствами. Примером может служить задача о синтезе оптимальной системы, т.е. системы, которая обладает наилучшими в некотором смысле свойствами. В этом случае критерий оптимальности формулируется в виде условий максимума (или минимума) некоторого функционала от свойств системы и ее реакции на внешнее воздействие при дополнительных ограничениях, накладываемых на другие функционалы или параметры системы. Необходимую информацию для решения четвертой задачи дает решение основной задачи.

11

Выбор метода для решения статистической задачи зависит от характера системы. Поэтому приведем классификацию систем, используя различные признаки.

В зависимости от того, как ведет себя система при одновременном приложении двух или нескольких воздействий, различают линейную и нелинейную системы. Система, описываемая операторным уравнением (В.1), называется линейной, если оператор Н удовлетворяет условиям:

где α – произвольное число; q1, q2 – внешние воздействия.

Для линейных систем справедлив принцип суперпозиции. Необходимо отметить, что из линейного характера дифференциального уравнения относительно выходного параметра еще не следует линейность оператора Н. В частности, если воздействие на систему является параметрическим, то такую систему трактуют как нелинейную [6].

Другой признак классификации получим, если будем рассматривать поведение системы во времени. По этому признаку системы бывают стационарные и нестационарные. Система называется стационарной, если ее свойства неизменны во времени. В этом случае оператор Н инвариантен относительно смещения начального момента времени. Оператор Н нелинейной системы этим свойством не обладает.

Можно провести классификацию систем, основываясь на аналитических свойствах оператора Н. Эти свойства могут быть связаны со структурой пространств входных и выходных параметров, но могут быть и не связаны. Различают вырожденные и невырожденные операторы. Например, оператор является вырожденным, если внешнее воздействие и поведение системы описываются конечным числом параметров, причем связь между этими параметрами выражается формулами, не содержащими ни дифференциальных, ни интегральных операций.

Наконец, еще одним признаком классификации является число измерений системы. Различают системы с конечным числом степеней свободы и системы с распределенными параметра-

12

ми. Последние подразделяются на системы одномерные, двухмерные и т.д. Поведение невырожденных дискретных систем описывается обыкновенными дифференциальными уравнениями, а поведение распределенных систем может описываться как обыкновенными дифференциальными уравнениями (в случае квазистатического воздействия на одномерные системы), так и уравнениями в частных производных. Существенным моментом в последнем случае является постановка краевых условий. Для распределенных систем обычно употребляют термин «стохастическая краевая задача».

В настоящее время разработано большое число методов решения линейных задач статистической механики [9, 14]. Это квазистатические, корреляционные и родственные им методы, а также методы, основанные на использовании кинетических уравнений. Каждый метод имеет свои достоинства и недостатки, свою область применения. Эти области могут перекрываться.

Методы первой группы (квазистатические методы) основаны на применении хорошо известных формул теории вероятности. Эти методы с успехом могут быть применены к тем задачам, в которых случайные факторы описываются при помощи конечного количества случайных величин. Для того чтобы использовать квазистатические методы, необходимо располагать решениями соответствующих детерминистических задач для всей области изменения случайных параметров. Дальнейшие операции сводятся к преобразованию распределения вероятностей этих параметров. Область применения квазистатических методов не ограничивается теми задачами, где нагрузки изменяются весьма медленно. Если случайные динамические нагрузки могут быть представлены в виде детерминистических функций времени, зависящих от конечного числа случайных величин, то квазистатические методы и здесь могут оказаться весьма эффективными.

Методы второй группы – корреляционные методы – основаны на использовании связи между корреляционными функциями входных (например, нагрузок) и выходных (прогибов,

13

напряжений и т.д.) параметров. Эти связи могут выражаться как при помощи дифференциальных и интегродифференциальных уравнений, так и (в простейших случаях) при помощи конечных соотношений. Спектральный метод и метод канонических разложений занимают промежуточное положение между корреляционными и квазистатическими методами. Область применения корреляционных методов – задачи, в которых внешняя нагрузка представляет собой корреляционный случайный процесс. Методы оказываются особенно удобными, если действие нагрузки является гауссовым процессом, а система – линейной. Однако и для ряда нелинейных систем иногда удается получить эффективное решение, привлекая методы линейной механики.

В третьей группе методов используются дифференциальные и интегродифференциальные уравнения, описывающие эволюцию функций распределения случайных параметров во времени. Эти методы хорошо разработаны применительно к процессам без последействия (марковским процессам). Поэтому область эффективного применения этих методов – задачи, в которых выходные величины можно трактовать как компоненты марковского процесса.

14

1. КВАЗИСТАТИЧЕСКИЙ ВЕРОЯТНОСТНЫЙ РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ

(В РАМКАХ СЛУЧАЙНЫХ ВЕЛИЧИН)

Под квазистатическими задачами будем понимать задачи,

вкоторых случайные факторы описываются при помощи конечного числа случайных величин. Будем полагать, что известна детерминированная зависимость между указанными группами параметров.

Система, удовлетворяющая этим условиям, является вырожденной. Нахождение характеристик для выходных параметров

вэтом случае сводится к применению известных формул теории вероятностей, дающих распределение случайных функций от случайных величин. Приведем некоторые сведения из теории вероятностей.

1.1. Случайные величины и их характеристики

Напомним, что случайной называют величину, которая в результате опыта может принять то или иное значение, заранее неизвестное. Она может быть как дискретной, так и непрерывной. Случайная величина полностью определена с вероятностной точки зрения, если известно, с какой вероятностью возможно появление каждого из принимаемых случайной величиной значений.

15

При решении прикладных вероятностных задач часто бывает необходимо определить вероятность того, что случайная величина Х примет значение, заключенное в некотором ограниченном интервале, например в интервале (a, b). Условимся для определенности левый конец a включать в интервал, а правый не включать. Тогда вероятность попадания случайной величины Х в интервал (a, b)

P(a X b) F(b) F(a).

Плотностью распределения непрерывной случайной величины называют функцию

Устремив верхний предел к бесконечности, получим:

F(x) f (y)dy 1.

Вероятность того, что случайная величина Х находится в интервале (x1 , x2 ),

Рассмотрим известный нормальный закон изменения плотности вероятности (закон Гаусса). Таким законом часто описываются результаты измерений каких-либо величин, механические характеристики материалов, нагрузки на машины и детали машин, сроки службы деталей и т.д. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях. Можно доказать, что сумма достаточно большого числа независимых или слабо зависимых случайных величин,

16

подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону, если дисперсия случайных величин примерно одного порядка.

Интегральная функция распределения при нормальном законе распределения определена на всей осии имеет следующий вид:

где mx – математическое ожидание; σх – среднее квадратичное отклонение случайной величины.

Сделаем замену: (x mx )2 t2 x mx t x x mx t x ,

2x

тогда

2

где t x mx .

x

Эта функция табулирована (прил. 4), а вероятность попадания случайной величины в интервал (х1 Х х2 ) может быть определена следующим образом:

Нетрудно показать, что вероятность попадания случайной величины Х на отрезок (mx , mx 3 x ) приблизительно равна 0,5.

Это означает, что для нормального распределения случайной величины все рассеяние практически укладывается на участок ( mx 3 x ) . Полученный результат позволяет по известным

17

значениям математического ожидания и среднего квадратичного отклонения случайной величины приближенно указать интервал ее возможных значений (правило трех сигм) (рис. 1.2).

Функция распределения случайной величины и ее плотность вероятности являются различными формами выражения закона распределения случайной величины. Наиболее часто применяемые на практике законы распределения приведены в прил. 1.

Однако приведенная выше исчерпывающая характеристика не всегда может быть получена либо из-за ограниченности экспериментальных результатов, либо из-за сложности проведения экспериментов, либо из-за большой их стоимости.

В этих случаях вместо законов распределения используют приближенное описание случайной величины, полученное с помощью минимального числа неслучайных характеристик, отражающих наиболее распространенные особенности распределений, например среднее значение, относительно которого группируются возможные значения случайной величины, или число, характеризующее степень разброса случайной величины около ее среднего значения.

Простейшей числовой характеристикой случайной величины является ее математическое ожидание. Для непрерывной случайной величины Х математическое ожидание

Геометрический смысл математического ожидания – центр тяжести площади, ограниченной кривой плотности распределения и осью абсцисс.

Для характеристики разброса значений случайной величины в данной серии опытов можно взять среднее значение какой-

18

нибудь положительной меры отклонения случайной величины от ее среднего значения, например квадрат разности между значениями случайной величины и ее средним значением. В результате получим величину, которая называется дисперсией.

Для непрерывной случайной величины дисперсия

При практических расчетах удобно использовать величинуx Dx , которая называется средним квадратичным отклонени-

ем. Геометрический смысл этой величины – центральный момент площади, ограниченнойкривой распределения и осью абсцисс.

Вероятность отклонения случайной величины от ее среднего значения на некоторую величину можно оценить, воспользовавшись формулой П. Чебышева:

Математическое ожидание и дисперсия имеют следующие свойства:

1.M[c] cf (x)dx c f (x)dx c;

где с – константа; Х – случайная величина.

19

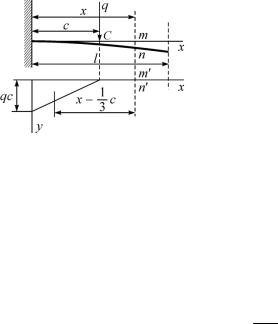
Пример 1.1. Балка (рис. 1.3), имеющая постоянную изгибную жесткость EI , нагружена случайной поперечной силой q с известными значениями математического ожидания mq и дис-

персии Dq.

Определить математические ожидания и дисперсии максимального прогиба и прогиба в точке приложения силы, а также максимального нормального напряжения.

Решение. Найдем прогибы и нормальные напряжения согласно известным соотношениям из сопротивления материалов.

Для консоли длиной l с сосредоточенным грузом q в поперечном сечении, отстоящем на расстоянии с от опоры, эпюра изгибающих моментов показана на рис. 1.3. Прогиб для какого-либо сечения определяется по уравнению

Для сечения слева от точки приложения нагрузки (точки С) вместо l используем с. Для какого-либо сечения справа от груза изгибающий момент и кривизна равны нулю; следовательно, эта часть балки остается прямой. Угол наклона является постоян-

Действительно, если на втором участке угол наклона постоянен, то

20