Вероятностные методы расчета конструкций

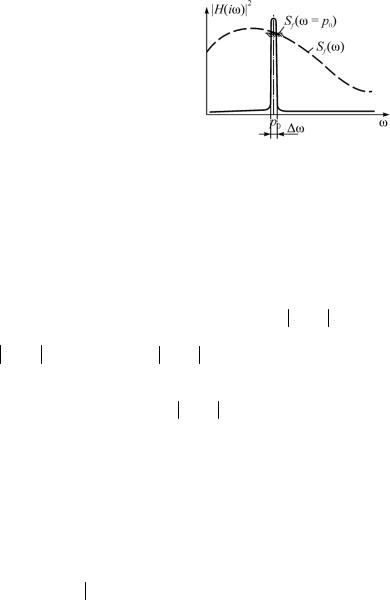
оси эта величина мало отличается от нуля (рис. 3.4). Такие системы называются системами с высокими фильтрующими свойствами или узкополосными системами, которые пропускают главным образом составляющие спектра внешнего воздействия с частотами, близкими

к собственной частоте колеба- Рис. 3.4 ний (резонансный режим).

Свойством узкополосности пользуются довольно часто, так как оно позволяет значительно упростить расчетные формулы, не внося при этом погрешностей, имеющих практическое значение.

Ширину полосы пропускания системы , или, как еще говорят, эффективную полосу пропускания системы, можно вычислить, разделив площадь под графиком H (i ) 2 , равную

H (i ) 2 d , на значение H (i ) 2 при p0 :

0

H (i ) 2 d

Конструкции из металлов и даже из железобетона являются системами с высокими фильтрующими свойствами (узкополосными), поэтому многие машиностроительные конструкции могут быть отнесены к узкополосным динамическим системам.

Для рассматриваемого случая

91

Подставляя (3.29) и соотношение (3.27) в формулу (3.28), получим дисперсию перемещения:

функция, не имеющая разрывов и очень резких максимумов вблизи p0 , то произведение H (i ) 2 S f ( ) , входящее под знак

интеграла в формуле (3.28), будет существенно отлично от нуля только вблизи p0 . Поэтому, если пренебречь изменением

спектральной плотности воздействия в пределах полосы пропускания (см. рис. 3.4) и принять ее равной значению на частотеp0 , то формула (3.30) примет вид:

В качестве примера рассмотрим движение транспорта по неровной дороге. Нет надобности доказывать, что неровности всех видов автомобильных и железных дорог носят случайный характер. Поэтому все задачи определения транспортных нагрузок опираются на теорию случайных процессов.

Пример 3.3 [21].

Рассмотрим случайные поперечные колебания прицепа (рис. 3.5, а) массой m при движении его со скоростью v по дороге, характеризующейся заданной спектральной функцией неровностей. Будем считать, что точка крепления прицепа к автомобилю (точка О), находящаяся на расстоянии l от его центра тяжести, не имеет вертикальных перемещений, жесткость шин весьма велика по сравнению с жесткостью рессор с. Момент инерции массы прицепа относительно точки О равен J0. В рес-

92

сорах возникает вязкое трение с коэффициентом трения . Массой колес прицепа по сравнению с массой m можно пренебречь. При решении будем считать, что в результате статистических исследований получена спектральная плотность воздействия дороги на систему:

где v – скорость движения; a, b – характеристики спектральной функции профиля дороги.

Рис. 3.5

Определить среднеквадратичное отклонение угла колебаний и угловой скорости колебаний прицепа в зависимости от скорости движения. Провести анализ зависимости среднеквадратичного отклонения угла колебаний от жесткости рессоры (при заданной скорости движения).

Параметры системы: J0 = 5·104 кг·см·с2; l = 250 см; а = = 10 см2 /м; b = 25 1/cм2; с = 200 кг/см; = 10 кг·с/см.

93

Решение. Представим прицеп в виде схемы (рис. 3.5, б), причем h значительно меньше l (поворот на угол приводит

только к вертикальному смещению точки А). Тогда уравнение малых угловых колебаний системы можно записать в виде:

Зависимость спектральной плотности выхода от спектральной плотности входа определяется зависимостью (3.27), т.е. в нашем случае

S ( ) H (i ) 2 Sh ( ),

где H (i ) 2 – квадрат модуля частотной характеристики систе-

мы, которая равна передаточной функции. Передаточная функция

в выражение спектральной плотности воздействия дороги на систему:

94

Находим дисперсию угла колебаний прицепа:

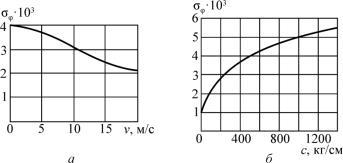
Рис. 3.6

График изменения среднеквадратичного отклонения угла колебаний в зависимости от скорости движения показан на рис. 3.6, а, а в зависимостиот жесткостирессорыс– нарис. 3.6, б.

3.2.2. Системы с n степенями свободы

Рассмотренные решения можно обобщить для случая динамической системы с n степенями свободы. Принципиальных затруднений при этом не возникает, но усложняется процесс вычислений.

Система дифференциальных уравнений движения системы имеет следующий вид:

При исследовании колебаний системы с n степенями свободы возможно несколько характерных случаев действия сил. Наиболее простой из них – это случай, когда все силы изменя-

95

ются по времени одинаково, дисперсии же сил могут быть разными. Другим случаем является вариант разных fi (t) , но статистически независимых между собой. Общим случаем и наиболее сложным является вариант, когда все силы fi (t) различны

и между ними существует сильная статистическая взаимосвязь. При решении первых двух вариантов используется метод главных координат [15, 17], который позволяет перейти от системы (3.31) к системе уравнений вида:

где pk – собственная частота колебаний; qk (t) – главные координаты, связанные с исходными координатами соотношением

k 1

uik – амплитудное смещение i-й массы при k-й форме собственных колебаний; Mk – обобщенная масса системы при k-й форме собственных колебаний,

i 1

Определение вероятностных характеристик решения уравнений (3.31) было рассмотрено ранее, следовательно, используя связь (3.32), можно найти вероятностные характеристики исходной системы.

Пример 3.4. Рассмотрим балку с двумя сосредоточенными массами. На массу m2 ( m2 m1 m ), расположенную на расстоянии 2l от заделки, внезапно подействовала случайная сила

96

f (t) f0 H (t) , где H (t) – функция Хевисайда (рис. 3.7). Вероятностныехарактеристикислучайной силы f0 известны ( mf0 , Df0 ).

Рис. 3.7

Определить математическое ожидание и дисперсию максимального нормального напряжения в заделке.

Решение. Уравнения колебаний:

Определим коэффициенты влияния:

Найдем собственные частоты колебаний системы:

Собственные формы колебаний:

u1 (u11;u21 ) (1; 3,132); u2 (u12 ;u22 ) (1; 0,319).

Перейдем к главным координатам по формуле (3.32):

где qk – главные координаты; uik – смещение i-й массы при k-й форме собственных колебаний.

97

Уравнения движения системы (3.35) с учетом (3.33) и (3.34) в главных координатах примут вид:

Решая полученные уравнения при нулевых начальных условиях, получим:

Определяем перемещения масс при колебаниях:

Изгибающий момент в заделке:

Ml( m1 y1 ) 2l( m2 y2 f0 )

f0l(2,774cos p1t 0,236cos p2t 2) F(t) f0 .

Максимальное напряжение в заделке max M F(t) f0 .

Wx Wx

Математическое ожидание и дисперсия этого напряжения:

98

Считая, что max распределено по нормальному закону, находим максимально возможное напряжение в заделке:

Пример 3.5. Рассмотрим ту же балку с двумя сосредоточенными массами. На массы m1 и m2 ( m2 m1 m ) внезапно подей-

ствовали случайные силы f1 (t) и f2 (t) (рис. 3.8). Определить

математическое ожидание и дисперсию смещения каждой из масс, если известны вероятностные характеристики внешних сил.

Рис. 3.8

Решение. Уравнения движения масс:

Рассмотрим различные варианты действия внешних сил. 1. Пусть внешние силы одинаково изменяются во времени,

но отличаются дисперсиями, т.е.

fi (t) Fi (0) f (t) ( i 1,2 ),

где Fi (0) – стандарт силы fi (t); f (t) – стационарная случайная

функция времени.

Здесь, как и в предыдущей задаче, удобно использовать метод главных координат. Переходя к уравнениям движения системы в главных координатах, получим:

99

j1

F1 (0) 0,319F22 (0) f (t) R2 f (t). m(1 0,319 )

Для определения коэффициента передачи k-й формы в стационарном режиме положим f (t) ei t , а qk (t) Hk (i )ei t .

Поскольку силы трения в задаче отсутствуют, то матрица передаточных коэффициентов имеет диагональный вид:

Hk (i ) pk2 Rk 2 .

Перемещение масс при колебаниях (3.36)

Из полученного соотношения следует, что коэффициент передачи для координаты yi

k 1 ( pk )

100