
Математический анализ в задачах и упражнениях
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
Л.М. Култышева, В.П. Первадчук, М.А. Севодин
МАТЕМАТИЧЕСКИЙ АНАЛИЗ В ЗАДАЧАХ И УПРАЖНЕНИЯХ
Утверждено Редакционно-издательским советом университета
в качестве учебно-методического пособия
Издательство Пермского национального исследовательского
политехнического университета
2013
1
elib.pstu.ru
УДК 517.38 К90
Рецензенты:
д-р физ.-мат наук, проф. А.Р. Абдуллаев (Пермский национальный исследовательский политехнический университет);
канд. пед. наук, доцент В.Л. Пестерева (Пермский государственный гуманитарно-педагогический университет)
Култышева, Л.М.
К90 Математический анализ в задачах и упражнениях : учеб.-метод. пособие / Л.М. Култышева, В.П. Первадчук, М.А. Севодин. – Пермь : Изд-во Перм. нац. исслед. поли-
техн. ун-та, 2013. – 172 с.
ISBN 978-5-398-00986-6
Охвачены следующие разделы: введение в анализ, дифференциальное исчисление функции одной переменной (неопределенный и определенный интеграл), ряды (числовые и функциональные).
Изложены методы и принципы решения основных типов задач. Каждый раздел содержит необходимые подробные примеры решения задач.
Предназначено для студентов первого курса. Может быть использовано для домашней самостоятельной работы студентов, самостоятельных и контрольных работ на занятиях.
УДК 517.38
ISBN 978-5-398-00986-6 |
© ПНИПУ, 2013 |
2
elib.pstu.ru
|
СОДЕРЖАНИЕ |
|
1. |
Пределы последовательностей и функций................................. |
4 |
|
1.1. Предел последовательности................................................ |
4 |
|
1.2. Предел функции................................................................... |
6 |
Контрольные задания к теме 1 ...................................................... |
14 |
|
2. |
Исследование и построение графиков функций...................... |
38 |
Контрольные задания к теме 2 ...................................................... |
57 |
|
3. |
Неопределенный интеграл......................................................... |
65 |
Контрольные задания к теме 3 ...................................................... |
78 |
|
4. |
Определенный интеграл ............................................................ |
95 |
|
4.1. Вычисление площадей плоских фигур............................ |
96 |
|
4.2. Вычисление длин дуг плоских кривых.......................... |
100 |
|
4.3. Вычисление объемов тел................................................. |
102 |
|
4.4. Вычисление площади поверхности вращения.............. |
104 |
5. |
Несобственные интегралы....................................................... |
108 |
Контрольные задания к темам 4, 5.............................................. |
112 |
|
6. |
Числовые и функциональные ряды........................................ |
128 |
|
6.1. Знакопостоянные ряды.................................................... |
128 |
|
6.2. Знакопеременные ряды.................................................... |
134 |
|
6.3. Функциональные ряды.................................................... |
140 |
|
6.4. Степенные ряды............................................................... |
145 |
|
6.5. Приложения рядов........................................................... |
150 |
Контрольные задания к теме 6 .................................................... |
154 |
|
3
elib.pstu.ru
1. ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ
1.1. Предел последовательности Пример 1. Используя определение предела, показать, что
lim |
n |
|
1. Найти N . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Обозначим |
x |
|
|
|
n |
. Пусть задано |
> 0, рас- |
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
n |
|
n 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
смотрим |
неравенство |
|
1 x |
|
|
|
|
|
1 |
< . Оно |
равносильно |
||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
n |
|
|
|
1 |
n |
|
||
n |
1 |
|
|
|
|
|
|
|
|
|
|
||||
. Следовательно, можно положить |
|
||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
, |
1, |
|
||||||
|
|
|
|
1 |
|
|
|
|
|
(1) |
|||||
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
||
Здесь через [x] обозначено наибольшее целое число, не превосходящее x.
Пример 2. Используя определение предела, показать, что
lim |
|
n2 |
|
1. |
Найти N( ) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Воспользуемся неравенствами |
|
|
|
|||||||||||||||||||||||
|
|
1 y |
|
|
|
n2 |
|
|
n2 |
|
|
n |
|
x |
|
0. |
|||||||||||
|
|
n |
n2 n 1 |
n2 n |
1 n |
n |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 yn |
|
|
|
|
1 xn |
|
. |
|
|
|
(2) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Пусть задано 0 . Найдем такое |
|
N, чтобы при n N вы- |
||||||||||||||||||||||||
полнялось неравенство |
|
1 xn |
|
|
. Из решения примера 1 следу- |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
ет, что N может быть определено согласно (1). Учитывая нера-
4
elib.pstu.ru
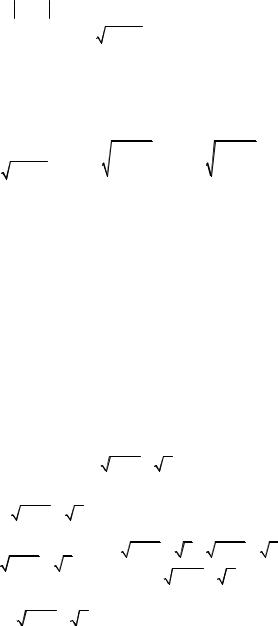
венство (2), заключаем, что при n N выполняется требуемое неравенство 1 yn .
Пример 3. Найти lim |
3 |
n2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
; |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
n 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Имеем неопределенность вида |
|
|
|
. Выполним |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следующие преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n |
|
|
1 |
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||
3 |
n2 n |
n |
|
n2 |
|
n |
n2 |
|
||||||||||||||||
|
|
|
|
|
|
|
lim |
|
|
|
|
|
0 . |
|||||||||||
lim |
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
n 2 |
n |
|
|
|
|
2 |
|
|
|
|
n |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||
Итак, искомый предел равен нулю.
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
Пример 4. Найти lim |
2 |
22 |
|
|
2n |
. |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
Решение. Применяя формулу для суммы n членов геомет- |
|||||||||||||||||||||||||||||||||
рической прогрессии, находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
lim 1 |
2 |
1 |
2 |
2 |
|
2 |
n |
|
|
|
1 |
|
|
|
|
1 |
|
|
4 . |
||||||||||||||
|
|
|
2 |
n 1 |
|
||||||||||||||||||||||||||||
|
|
|
lim |
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||
n |
1 |
|
|
1 |
|
3 |
2 |
|
|
|
3 |
n |
|
n |
|
|
|
1 |
|
1 |
|
3 |
|
||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
Пример 5. Найти lim |
|
n a |
n |
|
; |
. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Умножив числитель и знаменатель (знаменатель |
|||||||||||||||||||||||||||||||||
равен 1) на |
n a |
|
n , находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
lim |
|
n a |
n |
|
lim |
|
n a n |
n a n |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
n a |
n |
|
|
|
|
|||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a lim |
|
|
|
1 |
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n |
a |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
elib.pstu.ru
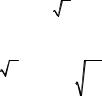
Пример 6. Найти lim |
n |
|
|
cos n |
. |
|
|
1 |
|||||
n n |
n |
|
||||
Решение. Предел lim |
|
n |
|
найден в примере 1. Второе сла- |
||
|
|
|
||||
n n 1 |
|
|
|
|
||
гаемое, стоящее под знаком предела, можно рассматривать как произведение ограниченной последовательности cos n и бес-
конечно малой 1 . Следовательно, второе слагаемое является
n
бесконечно малой последовательностью и предел ее равен нулю. Окончательно
lim |
n |
|
cos n |
|
lim |
|
n |
lim cos n |
1. |
|||||||
|
|
|
|
|||||||||||||
n n 1 |
|
n |
|
|
n n 1 |
n |
|
n |
|
|||||||
|
|
|
1.2. Предел функции |
|
|
|
||||||||||
Пример 7. Найти |
|
2x 3 3 3x 2 2 |
|
|
|
|||||||||||
lim |
|
|
|
|
|
|
|
|
; |
|
. |
|||||
|
|
x |
5 |
5 |
|
|||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||
Решение. Разделим и числитель и знаменатель выражения, стоящего здесь под знаком предела, на x5 – наивысшую степень этих многочленов. Получим
|
|
|
|
|
|
3 3 |
|
2 2 |
|
|
|
lim |
2x 3 3 3x 2 2 |
= lim |
|
2 |
|
x |
3 |
x |
|
2332 |
72 . |
x5 5 |
|
|
|
|
5 |
|
1 |
||||
x |
x |
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
Аналогичный прием во многих случаях можно применять и для дробей, содержащих иррациональности.
Пример 8. Найти lim |
2x 3 |
|
|
|||
|
|
|
|
; |
. |
|
|
|
3 |
x |
|||
x x |
|
|
|
|||
|
|
|
|
|
|
3 |
|
|
|
Решение. lim |
2x 3 |
lim |
|
|
2 x |
|
|
2. |
|
|
|
|
|
|
|
||||
x x 3 x |
x |
1 |
3 |
1 |
|
|
|||
|
|
|
x |
2 |
|
|
|||
|
|
|
|
|
|
|
|
||
6
elib.pstu.ru

Если P x и |
Q x |
– многочлены и P a Q a 0 , то при |
|||
|
|
|
|
|
|
отыскании |
lim |
P x |
|
рекомендуется разделить один или не- |
|
|
|||||
|
x a Q x |
|
|||
|
|
|
|
|
|
сколько раз числитель и знаменатель на x a . |
|
|
|
||||||||||||
|
Пример 9. |
Доказать |
(найти |
|
) |
равенство |
|||||||||
|
x2 |
6x 8 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
2 ; |
. |
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
||||
x 2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Сократив числитель и знаменатель на x 2 , при- |
||||||||||||||
ходим |
к рассмотрению |
предела |
|
при x 2 |
функции |
||||||||||
f x x 4 . Затем для 0 находим |
|
f x 2 |
|
|
|
x 4 2 |
|
|
|||||||
|
|
|
|
||||||||||||
x 2 . Следовательно, .
Выражения, содержащие иррациональности, во многих случаях приводятся к рациональному виду путем введения новой переменной.
Пример 10. Найти lim |
x2 |
x |
; |
0 |
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
x 1 |
|
|
|
|
||||||||||
|
|
|
x 1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
Решение. Введем новую переменную y |
x . Тогда |
||||||||||||||
lim |
x2 |
x |
= lim |
y y3 1 |
|
lim y |
|
y2 |
y 1 |
3. |
|||||
x 1 |
x |
1 |
y 1 |
y |
1 |
|
y 1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
Другим приемом нахождения предела от иррационального выражения является перевод иррациональности из числителя в знаменатель или, наоборот, из знаменателя в числитель.
Пример 11. Найти lim |
x h |
x |
, x |
|
0 |
|
|
|
|
|||
|
|
|
0 ; |
|
. |
|
|
|
||||
|
h |
|
0 |
|
|
|
||||||
|
h 0 |
|
|
|
|
|
|
|
|
|||
Решение. lim |
x h |
x |
= lim |
|
h |
|
|
|
|
|
1 |
. |
h |
|
h |
|
|
x |
|
||||||
h 0 |
|
h 0 |
x h |
|
2 x |
|||||||
Пределы функций, содержащих тригонометрические выражения, часто ищут с помощью первого замечательного предела.
Этот предел удобно представить в виде lim sin v |
1, |
где v – |
|
x a |
v |
|
|
|
|
|
7 |
elib.pstu.ru
функция независимой переменной x , и v 0 при x a . Первый замечательный предел используют для раскрытия неопре-
деленностей вида 00 .
Пример 12. Найти |
lim |
1 cos x |
; |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x |
2 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Учитывая формулу 1 cos x 2sin2 |
|
x |
, находим |
|||||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
||||||||
|
|
1 cos x |
|
|
2sin |
|
|
|
|
|
|
|
|
1 |
|
|
|
sin |
|
|
|
|
1 |
|
|
|||||||||||||
lim |
= |
lim |
|
|
2 |
|
|
lim |
2 |
|
|
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x2 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
2 x 0 |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
Пример 13. Найти |
lim |
arcsin 2x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
5x |
|
|
|
; |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. Введем новую переменную |
|
z arcsin 2x . Тогда |
||||||||||||||||||||||||||||||||||||
sin z 2x , |
x |
sin z |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim arcsin 2x |
= lim |
|
|
|
|
z |
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
2 . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 lim sin z |
|
|
|
|||||||||||||||||||||||
|
x 0 |
5x |
|
z 0 5 sin z |
|
|
|
|
|
|
|
|
5 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
z 0 |
|
|
z |
|
|
|
|
|
|
|
|
||||
Если |
ищется |
предел |
функции |
при x a, a 0 , |
то для |
|||||||||||||||||||||||||||||||||
удобства можно перейти к новому аргументу |
y x a , |
предел |
||||||||||||||||||||||||||||||||||||
которого равен нулю при x a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 14. Найти lim x |
4 |
tg2x ; 0 . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Положим x |
y , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x |
tg2x lim ytg |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x |
|
|
4 |
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim y ctg2 y |
|
|
1 lim |
2 y |
cos 2 y |
|
|||||
y 0 |
|
|
2 y 0 sin 2 y |
|
|
8
elib.pstu.ru
|
1 lim |
2 y |
lim cos 2 y |
|
|
1 . |
|
||||||
|
2 y 0 sin 2 y |
y 0 |
|
|
2 |
|
Для раскрытия неопределенностей вида 1 используют второй замечательный предел. Данный предел запишем в виде
1 |
|
|
|
|
1 |
|
v |
lim 1 v v |
e , где |
v 0 при |
x a ; или |
lim 1 |
v |
|
e , если |
x a |
|
|
|
x a |
|
|
v при x a. Здесь v – функциянезависимойпеременной x .
x 5 |
3x |
|
||
Пример 15. Найти lim |
|
|
; |
|
x 1 |
1 . |
|||
x |
|
|
|
|
Решение. Имеем
x 5 |
3x |
|
|
|
6 3x |
|
||||
lim |
|
|
lim 1 |
|
|
|
||||
x 1 |
x 1 |
|||||||||
x |
|
|
x |
|
|
|
||||
|
|
6 |
|
|
x 1 |
6 |
3x |
|
|
|
6 |
|
x 1 |
||||
lim 1 |
|
|
|
|
|
|
||
x 1 |
|
|
||||||
x |
|
|
|
|
||||
18 x
lim ex 1 e18 .
x
Пример 16. Найти lim x 3 ln x 1 ln x 2 .
x
Решение. Учитывая свойства логарифмов, находим
|
x |
x |
|
3 |
|
ln |
|
|
|
ln |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
lim |
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
1 |
|
x 3 |
|
|
|
|
|
|
|
1 |
1 |
|
x 3 |
|
|
|
|
|
|
|||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
lim ln |
|
|
|
|
|
|
|
|
ln lim |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|||||||||||||||||||||
|
x |
1 2 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 x |
|
|
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
lim 1 |
x |
|
|
1 |
|
|
|
|
|
|
e 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ln |
x |
|
|
|
|
|
|
|
|
|
x |
|
ln |
|
|
|
|
ln e3 |
3. |
|
|
|
|
||||||||||
|
|
|
2 x |
|
|
|
|
|
e 2 1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
lim 1 |
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь мы воспользовались тем положением, что если суще- |
|||||||||||||||||||||||||||||||||
ствует и положителен |
x a |
f |
|
x |
|
, то |
|
x a |
ln f |
|
x |
|
ln |
x a |
|
x |
|
. |
|||||||||||||||
lim |
|
|
|
|
lim |
|
|
|
|
lim f |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
elib.pstu.ru
Пример 17. Найти lim |
2cos2 x 1 |
; |
0 |
|
. |
|||
ln sin x |
|
0 |
|
|||||
|
|
|
|
|||||
x |
2 |
|
|
|
|
|||
Решение. Воспользуемся известными равенствами (следствиями второго замечательного предела)
lim |
loga 1 x |
loga e; |
lim ax 1 |
ln a. |
||
x |
||||||
x 0 |
|
x 0 |
x |
|
||
Для этого введем новую переменную y cos2 x . Находим
|
2cos2 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
1 |
|
lim |
lim |
|
|
2y 1 |
|
|
|
2lim |
y |
|
|||||||
ln sin x |
1 ln |
|
|
|
|
|
|
ln 1 |
y |
||||||||
x 2 |
|
y 0 |
1 y |
|
y 0 |
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
y |
|
||
|
|
|
2y |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
2lim |
|
|
y |
|
|
|
|
2 ln 2 2ln 2. |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
y 0 ln |
|
y |
|
|
|
ln e |
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 18. Найти lim |
ex e x |
; |
|
0 |
|
|
|
||||||||||
|
|
sin x |
|
0 |
. |
|
|
|
|||||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
||||||
Решение. lim |
ex |
e x |
|
|
|
|
|
e2 x |
1 |
|
||||||
|
|
|
|
lim |
|
|
|
|
|
|
|
|||||
sin x |
|
ex sin x |
||||||||||||||
x 0 |
|
|
x 0 |
|
|
|||||||||||
lim |
e2 x 1 |
|
x |
|
|
2 |
|
|
|
|
||||||
|
2x |
|
sin x ex |
|
|
|||||||||||
|
x 0 |
|
|
|
|
|
||||||||||
2lim |
e2 x |
1 |
lim |
|
x |
lim |
1 |
2. |
||||||||
|
2x |
|
|
|
|
ex |
||||||||||
x 0 |
|
|
x |
0 |
sin x x 0 |
|
|
|||||||||
Для упрощения выкладок при нахождении пределов часто пользуются эквивалентностью функций. Напомним, что функ-
ция f x |
эквивалентна |
функции g x |
при x a |
(в этом слу- |
||
чае пишем |
f x g x |
при x a ), если lim |
f x |
1 . Извест- |
||
g x |
||||||
|
|
|
x a |
|
||
10 |
|
|
|
|
|
|
elib.pstu.ru
