
Математический анализ в задачах и упражнениях
..pdf
Пример 9. Вычислить длину петли кривой x 3t2 , y t t3 .
Решение. Если кривая задана уравнением в параметриче-
ской форме x x t , y y t и производные x t , y t |
не- |
||||
прерывны на отрезке t1; |
t2 , то длина дуги кривой вычисляется |
||||
t2 |
t 2 |
|
y t 2 dt. |
|
|
по формуле l x |
|
|
|
||
t1 |
|
|
|
|
|
Найдем пределы интегрирования t1 и t2 для нашего примера. |
|||||
Из условия x |
3t2 0 |
следует, что кривая лежит в правой |
|||
полуплоскости. Поскольку |
x t x t , y t y t , |
то кри- |
|||
вая симметрична относительно оси ОХ. Из равенства |
x |
3t2 |
|||
следует, что x t принимает одно и то же значение не более чем
2 раза. Это значит, что точки самопересечения кривой лежат на оси ОХ. Из условия у = 0 находим t1 0, t2 1, t3 1. Посколь-
ку x t2 x t3 3 , то точка 3; 0 является единственной
точкой самопересечения кривой. Стрелками на рисунке показано направление, в котором точка М(х; у) обходит кривую при
изменении |
t от до (рис. 15). Найденные значения |
t2 1 и t3 |
1 являются пределами интегрирования. |
Рис. 15. График кривой х |
3t2 , y t t3 |
101
elib.pstu.ru
Далее |
находим |
x t 2 |
|
3t, y t 1 3t2 , |
|
откуда |
|||||
x t 2 y t 2 dt |
1 6t2 9t4 |
|
1 3t2 . Следовательно, |
|
|||||||
|
l 1 1 3t2 dt t |
|
1 1 t3 |
|
1 1 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
Пример 10. Вычислить длину дуги кривой |
1 |
|
|
1 |
|
||||||
2 |
|
|
от |
||||||||
|
|
|
|
|
|
|
|
|
|
||
2 до 4 . |
|
|
|
|
|
|
|
|
|
|
|
Решение. Если кривая задана уравнением |
в поляр- |
||||||||||
ных координатах, то длина дуги кривой находится по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
l |
|
2 |
d . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем подынтегральное выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
d |
2 |
d |
2 |
|
2 |
d 2 |
|
|||||||||||||||||||
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
1d . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||||
Из уравнения кривой находим |
|
|
|
1 |
|
|
|
|
|
. Тогда |
|||||||||||||||||||||||||||||
d |
2 |
|
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
|
|
2 1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
4 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
l |
|
|
|
1 |
|
|
|
|
1d |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1d |
|||||||||||||||
|
4 |
|
2 |
|
4 |
|
|
|
2 |
|
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 4 |
|
|
|
1 |
2 |
d |
1 |
|
2 |
|
|
|
|
|
|
4 |
|
3 |
|
ln 2 |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4.3. Вычисление объемов тел
Объем тела выражается интегралом V b s x dx , где s x –
a
площадь сечения тела плоскостью, перпендикулярной к оси ОХ в точке x, a x b .
102
elib.pstu.ru
Объем тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной кривой y f x , осью ОХ и
прямыми x a и x b, выражается интегралом V b |
f 2 x dx. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
Объем тела, образованного вращением вокруг оси ОY криволи- |
||||||||||||||||||||||||||||||||||||||
нейной трапеции, |
ограниченной |
кривой |
|
x y , |
|
осью ОY |
||||||||||||||||||||||||||||||||
ипрямыми y c и y d, выражаетсяинтегралом V d 2 |
y dy. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
Пример 11. Найти объем эллипсоида |
x |
2 |
|
|
|
y2 |
|
z2 |
|
1. |
|
|
|
|
||||||||||||||||||||||||
a |
2 |
|
|
b2 |
c2 |
|
|
|
|
|
||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x const, |
|||||||||||||
Сечение |
эллипсоида |
|
плоскостью |
|
|
|||||||||||||||||||||||||||||||||
a x a, есть эллипс с уравнением |
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
1 |
||||||||||||
|
b |
2 |
|
|
|
|
|
x2 |
|
c |
2 |
|
|
|
|
x2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
a |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и полуосями b |
1 |
x2 |
|
и c |
1 |
x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||
Площадь сечения s x b 1 |
|
c |
1 |
|
|
|
|
bc |
1 |
|
x |
. |
||||||||||||||||||||||||||
a |
2 |
|
2 |
|
|
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
||||||
|
a |
|
2 |
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Тогда V bc 1 |
|
x |
dx |
bc x |
|
|
|
|
|
|
|
|
|
4 abc. |
|
|
|
|
|
|||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
a |
|
|
a |
|
|
|
|
|
|
|
|
3a |
|
|
|
a |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример |
12. |
Фигура, ограниченная |
|
|
|
|
|
дугой |
|
синусоиды |
||||||||||||||||||||||||||||
y sin x, осью ординат и прямой у = 1, вращается вокруг оси
ОY. Найти объем полученного тела вращения.
Решение. Уравнение кривой x arcsin y рассматривается на отрезке 0;1 . Поэтому
V 1 x2dy 1 arcsin y 2 dy.
00
Винтеграле проведем замену переменной, применяя под-
становку arcsin y t. |
Отсюда y sin t, dy costdt. Новые пре- |
103
elib.pstu.ru

делы интегрирования 0 и 2 . Полученный при этом интеграл вычислим методом интегрирования по частям.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
2 |
|
|
|
2 |
sin t |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
V t |
|
costdt t |
|
02 |
2 t sin tdt |
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2t cost |
|
2sin t |
|
|
|
|
2 |
|
||
|
4 |
|
2 |
|
2 |
|
|
4 |
2 . |
||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
||
4.4. Вычисление площади поверхности вращения
Площадь поверхности S, образованной вращением вокруг
оси ОХ дуги L кривой y y x |
a x b , выражается инте- |
||
гралом S 2 b |
y |
1 y 2 dx. |
|
a |
|
|
|
Эту формулу часто записывают в виде S 2 L ydl , где dl –
дифференциалдлины дуги.
Если кривая задана параметрически или в полярных координатах, то достаточно произвести замену переменной, выразив соответствующим образом дифференциал длины дуги:
|
|
2 |
|
2 |
|
|
x x t |
|
dl |
xt |
yt |
dt, |
если |
|
; |
||
|
|
|
||||||
|
|
|
|
|
|
|
y y t |
|
|
|
|
|
|
|
|
|
|
dl |
|
2 |
2 |
d , если . |
||||
|
|
|
||||||
Пример 13. Вычислить площадь поверхности, образован-
2 |
2 |
2 |
вокруг оси ОХ. |
ной вращением астроиды x3 |
y3 |
a3 |
Решение. Дифференцируя уравнение астроиды, получим
2 |
2 |
2 |
2 |
|
|
|
3 x |
3 |
3 y |
3 |
y |
0, |
|
|
|
|
104
elib.pstu.ru
откуда
|
2 |
|
|
|
|
|
|
y |
y3 |
|
|
|
|
||
|
|
. |
|
|
|
|
|
2 |
|
|
|
|
|||
|
x3 |
|
|
|
|
||
Далее найдем |
|
|
|
|
|
|
|
|
2 |
1 |
|
||||
1 y 2 1 |
y3 |
|
a3 |
. |
|||
2 |
1 |
||||||
|
|
x3 |
|
x |
3 |
|
|
Астроида симметрична относительно оси ОY, поэтому при вычислении площади поверхности можем считать x 0 , а затем удвоить результат.
Таким образом,
a |
|
|
|
3 |
|
|
|
2 |
2 |
2 |
1 |
1 |
|
S 4 a3 |
x3 |
|
a3 x |
3 dx. |
||
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
t2 ; |
|
|
Для вычисления интеграла используем замену a3 |
x3 |
||||
|
2 |
x |
1 |
|
|
|
|
3 |
3 dx 2tdt. |
|
|
|
|
||
|
Тогда получим |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
1 a3 |
12 a2 . |
|
|
|
|
|
|
S 12 a3 |
t4dt = |
|
|
|
|
|
|
|
0 |
5 |
|
|
|
|
Пример 14. Вычислить площадь поверхности тора, образо- |
|||||
ванного вращением окружности x2 y b 2 r2 (0 < r < b) во-
круг оси ОХ.
Решение. Запишем уравнение окружности в параметрической форме:
x r cost , y b r sin t. откуда xt r sin t , yt r cost.
105
elib.pstu.ru
Найдем площадь поверхности (рис. 16)
|
2 |
b r sin t |
r sin t 2 r cost 2 dt |
||||
S 2 |
|||||||
|
0 |
|
|
|
|
|
|
2 |
b r sin t dt 2 r bt |
|
02 r cost |
|
02 4 2br. |
||
2 r |
|
|
|||||
|
|
||||||
|
|
||||||
0 |
|
|
|
|
|
|
|
Рис. 16. Тор (пример 14)
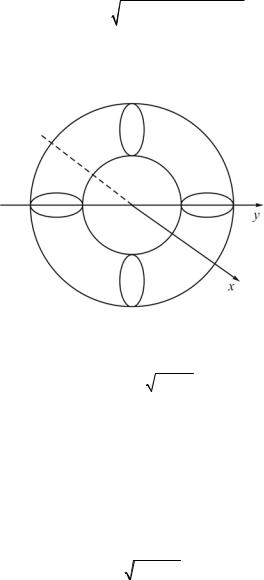
Пример 15. Вычислить площадь поверхности, образованной вращением лемнискаты a cos 2 вокруг полярной оси
(рис. 17).
Решение. Действительные значения для получаются при
условии cos 2 0, |
т.е. при |
|
(правая ветвь лемниска- |
||||||
|
|
|
|
|
4 |
|
|
4 |
|
ты) и |
3 |
|
5 |
(левая ветвь лемнискаты). |
|||||
|
4 |
||||||||
4 |
|
|
|
|
|
|
|
||
Площадь поверхности найдем по формуле |
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
S 2 y |
2 |
|
2 |
d . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
106 |
|
|
|
|
|
|
|
|
|
elib.pstu.ru
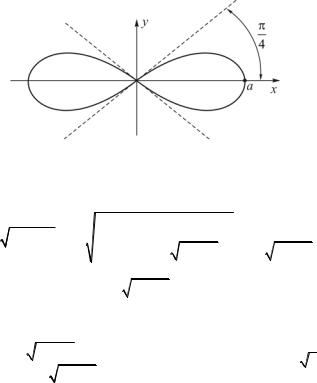
Рис. 17. Лемниската (пример 15)
Имеем
dl |
|
2 |
2 |
d a |
2 |
|
|
|
|
asin 2 |
2 |
ad |
|
|
||
|
|
|
|
cos 2 |
|
|
|
d |
|
|
|
. |
||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 |
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 |
|
|
|
|||
Далее y sin asin |
cos 2 . |
|
|
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 sin d 4 a2 cos 04 |
2 a2 |
2 |
2 . |
||||||||||
S 4 a2 |
||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
cos 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
107
elib.pstu.ru

5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Пример 1. Вычислить несобственный интеграл или установить расходимость.
Решение.
|
dx |
|
|
lim |
0 |
|
|
|
|
|
dx |
|
lim |
A |
|
|
|
dx |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x2 |
|
|
|
|
|
||||||
x2 2x |
5 |
|
B B |
x2 |
|
|
2x 5 |
A |
|
2x 5 |
|
|||||||||||||
|
lim |
1 arctg |
x 1 |
|
|
0 |
lim |
1 arctg |
x 1 |
|
|
A |
|
|||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
B 2 |
|
|
2 |
|
|
B |
|
A |
2 |
2 |
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 arctg 1 |
|
|
|
|
|
|
1 arctg 1 |
|
. |
|
|
|||||||||||
|
|
2 |
|
2 |
|
|
4 |
|
|
|
4 |
2 |
|
2 |
2 |
|
|
|
|
|
|
|||
|
Пример |
2. |
Исследовать |
сходимость |
интеграла |
||
x |
x 1 |
|
|
|
|
||
1 |
|
dx. |
|
|
|
||
x2 25 x4 1 |
|
|
|
||||
|
Решение. Для выяснения сходимости интеграла воспользуемся |
||||||
признаком сравнения: если при x непрерывная и неотрица- |
|||||||
тельная функция f x |
является бесконечно малой порядка по |
||||||
сравнению с функцией |
1 |
(т.е. lim |
f x |
c, 0 |
|
c |
|
), то инте- |
||
|
|
|||||||||
|
|
|||||||||
|
|
x |
x 1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
грал f x dx |
сходится при 1 ирасходитсяпри 1. |
|||||||||
a
Подынтегральная функция непрерывна и положительна при x 1. Определим ее порядок малости относительно 1x .
|
x x 1 |
1 |
|
|
1 |
1 |
|
|
1 |
|
|
|
|||
|
|
|
x |
x2 |
|
|
, то 1. Следо- |
||||||||
Поскольку |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
x2 25 x4 1 |
1 |
2 |
1 |
|
|
1 |
|
||||||||
|
|
|
x |
6 |
|
|
10 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
вательно, интеграл расходится.
108
elib.pstu.ru
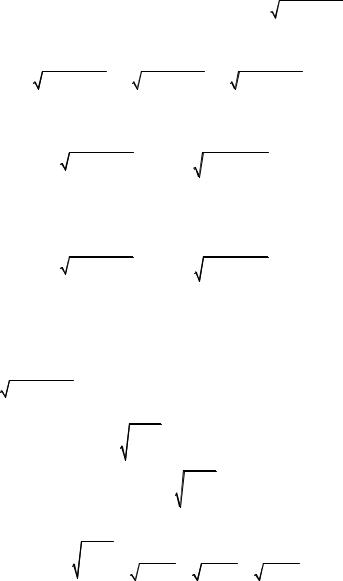
Пример 3. Исходя из определения вычислить несобствен-
ный интеграл (или доказать его расходимость) |
3 |
|
|
|
|
dx |
|
. |
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4x x |
3 |
||||
Решение. Представим интегралв видесуммыдвухинтегралов: |
|||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
dx |
|
|
2 |
|
|
|
dx |
|
|
|
3 |
|
dx |
|
|
|
. |
|
|
||||||||||
|
|
|
|
|
2 |
3 |
|
|
|
|
2 |
|
3 |
4x x |
2 |
|
|
|
|||||||||||||||||
|
1 |
|
4x x |
|
1 |
|
|
|
|
4x x |
2 |
|
3 |
|
|
|
|||||||||||||||||||
Вычислим каждое слагаемое в отдельности: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
4x |
x |
3 |
|
0 0 |
1 x 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
lim arcsin x 2 |
|
12 |
lim 0 arcsin 1 |
. |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
3 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
3 |
|
dx |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4x |
x |
3 |
|
0 0 |
1 x 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
lim arcsin |
x 2 |
|
32 |
lim |
arcsin 1 0 |
. |
|
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
0 0 |
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
dx |
|
|
|
|
|
|
– интеграл сходится. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
4x x |
|
3 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 4. Вычислить несобственный интеграл (или дока-
зать его расходимость) |
2 |
2 xdx . |
|
|
0 |
2 x |
|
Решение. Заметим, |
что |
lim |
|
|
|
|
x 2 0 |
дынтегральное выражение к виду
2 x . Преобразуем по-
2 x
f x |
2 x |
|
2 x |
|
2 |
|
x |
. |
2 x |
4 x2 |
4 x2 |
|
|||||
|
|
|
|
4 x2 |
||||
109
elib.pstu.ru
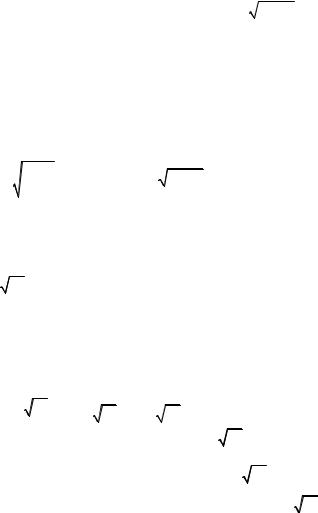
Отсюда видно, что функция F x 2arcsin |
x |
|
4 x2 яв- |
|
|||
2 |
|
|
|
ляется первообразной для функции |
f x на промежутке 0; |
2 . |
|||
Кроме того, функция F x |
непрерывна на |
отрезке |
0; |
2 , |
|
а функция f x непрерывна |
на |
промежутке |
0; 2 . |
Значит, |
|
можно применить обобщённую формулу Ньютона – Лейбница, по которой получим
|
|
2 |
|
|
2 x |
|
|
x |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 x |
dx 2arcsin |
|
|
|
4 x |
|
|
|
|
|
|
|
|
2 |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2arcsin1 2 2 |
|
2 |
2. |
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Пример 5. Исследовать сходимость несобственного инте- |
||||||||||||||
2 |
ln 1 |
5 |
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
грала |
|
|
|
dx. |
|
|
|
|
|
|
|
|
||
sin x |
1 |
|
|
|
|
|
|
|
|
|
||||
0 |
e |
|
|
|
|
|
|
|
x непрерывна и |
|||||
Решение. |
Подынтегральная функция f |
|||||||||||||
положительна на промежутке (0; 2]. Покажем, что lim f |
x : |
|||||||||||||
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
||
lim |
ln 1 5 x3 |
lim |
5 x3 |
lim |
5 x3 |
lim |
1 |
|
. |
|
||||
esin x 1 |
sin x |
x |
5 x2 |
|
||||||||||
x 0 |
x 0 |
x 0 |
x 0 |
|
|
|
|
|
||||||
Одновременно мы показали, что |
f x |
ln 1 5 |
x3 |
|
~ |
|
1 |
|||||||
|
|
|
|
|
|
|
|
esin x 1 |
5 |
x2 |
||||
при x 0 .
Используем теперь утверждение о том, что если функция
f x 0 |
определена и непрерывна на промежутке a; b |
и яв- |
||
ляется бесконечно большой порядка по сравнению с |
1 |
|
||
b x |
||||
|
|
|||
110 |
|
|
|
|
elib.pstu.ru
