Министерство образования и науки Российской Федерации Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Хабаровская государственная академия экономики и права»

Кафедра математики и математических методов в экономике

ДИСКРЕТНАЯ МАТЕМАТИКА

Учебное пособие

Хабаровск 2009

Министерство образования и науки Российской Федерации Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Хабаровская государственная академия экономики и права»

Кафедра математики и математических методов в экономике

ДИСКРЕТНАЯ МАТЕМАТИКА

Учебное пособие

Хабаровск 2009

2

ББК В И 25

Ивлева А. И. Дискретная математика : учеб. пособие / А. И. Ивлева. – Хабаровск : РИЦ ХГАЭП, 2009. – 120 с.

Рецензенты : д-р физ.-мат. наук, проф. Намм Р.В., канд. физ.-мат. наук, доцент Диреев Ю. В.

В учебном пособии изложены основные понятия теории множеств,

отношений и отображений, элементы теории графов и математической

логики. Основные положения каждого раздела иллюстрируются

примерами, в каждом разделе приведены задачи для самостоятельного

решения.

Содержание учебного пособия отвечает требованиям рабочей программы дисциплины «Дискретная математика» для студентов

специальности 061800 «Математические методы в экономике»

Утверждено издательским библиотечным советом академии в качестве

учебного пособия для студентов

© Хабаровская государственная академия экономики и права, 2009

3

Содержание

Введение ………………………………………………………………………. 4

Глава 1. Элементы теории множеств………………………………………….4

1.1Основные понятия теории множеств. Операции над множествами. Основные тождества алгебры множеств ………………...…..5

1.2Бинарные отношения. Свойства бинарных отношений ………...14

1.3Эквивалентность и порядок. Операции над бинарными отношениями ……………………..………………………..………………….18

1.4Соответствия ……………………..………………………..……….23

1.5Функции и отображения……………………..…………..………...26 Глава 2. Булева алгебра ………………………………………………………28

2.1Операции логики Буля……………..……………………………... 29

2.2Формы представления булевых функций……………..………….35

2.3Методы доказательств в логике Буля……………..………………38

Глава 3. Логика высказываний……………..……………………………..…42

3.1Классическая логика….…………..……………………………..…42

3.2Высказывания….…………..…………………………………….…46

3.3Формулы алгебры высказываний….…………..……………….…52

3.4Эквивалентные преобразования….…………..………………...…57

3.5Основные логические законы….…………….………....…………62

3.6.Необходимое и достаточное условие импликации ….………….65

3.7Нормальные формы формул логики высказываний….………….69

3.8Логическое следствие….………………………………………….72

Глава 4. Логика предикатов….……………...……………………………….77

4.1Основные понятия….…………….……………………..………….77

4.2Кванторы….…………….……………………..…………...……….82

4.3Формулы логики предикатов. Выполнимость и истинность….…88

4.4Эквивалентные соотношения. Префиксная нормальная форма…93

Глава 5. Теория графов…………………………………………………….…97

5.1Основные понятия теории графов. Способы задания графов…..97

5.2Операции над частями графа. Графы и бинарные отношения...103

5.3Маршруты, пути, цепи, циклы. Дерево и лес…………………...105

Библиографический список ....……………………………………………...118

4

ВВЕДЕНИЕ

При исследовании, анализе и решении многих реальных экономических и управленческих ситуаций широко используются дискретные методы формализованного представления, являющиеся предметом рассмотрения в дискретной математике. К ним относятся методы, основанные на теоретико-множественных представлениях, графы, алгоритмы, формальные системы, математическая логика и др. Несмотря на разнообразие подобных методов, общим в них является дискретность описания объектов анализа. Методы дискретной математики пригодны для описания и последующего конструктивного анализа многих проблемных ситуаций, в том числе не поддающихся описанию традиционными средствами классической математики, и позволяют при необходимости активно использовать современную вычислительную технику, новые информационные технологии.

Дискретная математика предлагает:

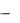универсальные средства (языки) формализованного представления;

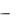способы корректной переработки информации, представленной на этих языках;

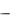возможности и условия перехода с одного языка описания явлений на другой с сохранением содержательной ценности моделей. Задачей курса является освоение будущими экономистами основных

моделей и методов формализованного представления: теоретико-

множественных, логических, графических. Теория множеств, логика,

теория графов являются фундаментом дискретной математики.

Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

В обычной речи мы часто употребляем слово «множество»: множество людей, множество книг, множество законов и т.д. Теория множеств создана в последней четверти XIX века чешским математиком С. Больцано, немецким ученым Г. Кантором и др. Данная теория была признана связующим звеном между логикой и математикой.

5

1.1 Основные понятия теории множеств. Операции над множествами. Основные тождества алгебры множеств

Теория множеств – это наука о множествах самой произвольной природы. Множество является одним из тех первоначальных, наиболее общих понятий, которые приходится принимать без определения, оно не может быть введено через другие понятия.

Под множеством понимается некоторая совокупность объектов, объединённых общим признаком и рассматриваемых как одно целое. Этот общий признак называется характеристическим.

Элементы множества могут иметь произвольную природу, не обязательно числовую. Например, множество людей, находящихся в аудитории.

Множества обозначаются обычно заглавными латинскими буквами: А, В, С, …, а их элементы – строчными: а, b, с, … .

Множества делятся на конечные и бесконечные в зависимости от того, является ли число элементов, входящих в их состав, конечным или же бесконечным. Например, множество участников соревнования конечно, а множество точек, лежащих в круге, бесконечно.

Вводится в рассмотрение также пустое множество, то есть не содержащее элементов. Оно обозначается Ø.

Множество может быть задано через перечисление его элементов. Например, множество обучаемых в учебной группе задаётся перечислением фамилий в журнале.

Запись А 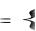означает, что множество А состоит из элементов а1 , а2 ,..., а10 .

Принадлежность элемента а множеству А задаётся обозначением а А. Отрицание этого факта обозначают а А.

Порядок перечисления элементов между фигурными скобками произвольный, т.е. {a, b, c, d} = {b, c, d, a}, но не допускается неоднократное перечисление одного элемента среди остальных элементов множества.

6

Во многих задачах выделяют некоторое свойство F элементов х множества Х такое, что каждый элемент либо обладает этим свойством, либо нет. При задании множества описанием его характеристических свойств между фигурными скобками после указания текущего значения элемента множества Х, т.е. х Х, ставится знак “ “, вслед за которым указывают характеристическое свойство элементов множества, т.е. F (х):

x X F(x) или x F(x) .

Например, запись

0,5

определяет множество таких значений х, что sin x > 0,5.

Множество, каждый элемент которого может приобрести индекс из множества натуральных чисел N={1,2,..., n,...}, называют счётным.

Число элементов счётного конечного множества A называют его мощностью и обозначают так: |A|=n. Например, мощность множества цифр равна 10, а мощность множества строчных букв латинского алфавита – 26.

Множества А и В называются равными, если каждый элемент множества А является элементом множества В, и обратно, каждый элемент множества В является элементом множества А. Принято обозначение

А = В.

Если все элементы множества A являются также элементами множества B, то множество A является подмножеством множества B. Это обозначают как A B, говорят A включено B.

Если A B и B A, то A=B.

Например, если А={1, 2, 3} и B={3, 2, 1}, то A=B.

Если A B и A B, то A называют собственным подмножеством B.

Это обозначают A B, говорят B строго включает A.

Например, если А={1, 2, 3} и B={1, 2, 3, 4, 5}, то A B .

Если, не все элементы множества A принадлежат множеству B, то

7

Если даны два множества Х и Y, то множество всех упорядоченных

Аналогично прямым произведением нескольких множеств X1, X2,...,Xn называется множество всех упорядоченных последовательностей

каждый его элемент – компонентой кортежа. Число компонент кортежа n определяет его длину или ранг. Для обозначения кортежа будем использовать круглые скобки. Длина пустого кортежа равна нулю. Кортежи длины n>1 называют n-кой (двойкой, тройкой, и т.д.).

Например, если X1={a, b, c, d, e, f, g, h} и X2={1, 2, 3, 4, 5, 6, 7, 8}, то прямое произведение этих множеств формирует 64 кортежа (x1, x2), однозначно определяющих каждую клетку шахматной доски, т.е.

(X1 X2)={(a,1) , (a,2) , ... , (h,7) , (h,8)}.

Два кортежа, имеющих одинаковую длину и одинаковые имена компонент, но различные их значения, называют совместимыми кортежами.

Два кортежа, имеющих одинаковую длину, одинаковые имена и одинаковые значения компонент, равны друг другу.

Над множествами, так же как и над числами, производят некоторые операции. Геометрическая иллюстрация операций над множествами была предложена великим математиком XVIII века петербургским академиком Леонардом Эйлером (1707 – 1783 гг.) и широко применялась английским математиком Джоном Венном (1834 – 1923 гг.). Поэтому такие рисунки называют диаграммами Эйлера – Венна.

8

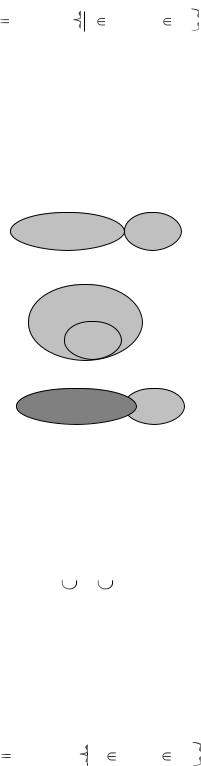
Диаграмма Эйлера – Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи – элементы, не принадлежащие этому множеству.

Объединением А В множеств А и В называется множество С, содержащее те и только те элементы, которые принадлежат хотя бы одному из множеств А или В:

С А В с с А или с В .

Союз «или» здесь не разделительный, то есть не исключается возможность одновременной принадлежности некоторых элементов и множеству А и множеству В. При этом такие элементы зачисляются в объединение С только один раз. Объединение часто называется суммой множеств. Объединение трёх и более множеств определяется аналогично.

Схематично эта операция изображена на рисунке 1.1.

А В

А

В

А В

Рисунок 1.1 – Объединение А В

Например, обозначим через А множество успевающих студентов в группе, через В – множество девушек в этой группе и через С – множество неуспевающих юношей. Тогда А В С является множеством всех учащихся этой группы. Множества А и В имеют общие элементы – успевающих девушек.

Пересечением А В множеств А и В называется множество С, содержащее те и только те элементы, которые принадлежат и А, и В одновременно:

С А В 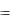с с А и с В .

9

Иными словами, пересечение образовано всеми общими элементами данных множеств. Аналогично определяется пересечение трёх и более множеств.

Схематично операция пересечения множеств представима в виде (рисунок 1.2):

А В

А

В

Рисунок 1.2 – Пересечение А В

Например, пусть А – множество юношей, обучающихся в институте, а В – множество юношей и девушек, обучающихся на 1-м курсе. Тогда пересечение А В – множество юношей, которые учатся на 1-м курсе.

Множества А и В называются непересекающимися, если

А В = Ø.

Разностью А\В двух множеств А и В (рисунок 1.3) называется множество С, состоящее из тех и только тех элементов, которые принадлежат А, но не принадлежат В:

С А \ В 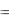с с А и с В .

В

А

А В

А

В

Рисунок 1.3 – Разность А\В

10