5543

A B , B = 0, следовательно A B истинно, только если погода холодная

(A = 0).

Пример 3.2. Укажите, какие из следующих предложений являются высказываниями, установите истинность простых высказываний. В сложных высказываниях выделите конъюнкцию и дизъюнкцию, установите истинность. Возьмите первые два высказывания и сформулируйте отрицание, конъюнкцию и дизъюнкцию.

1. 8 833 < 882 + 332.

3.«Треугольник называется равносторонним, если его стороны равны между собой».

4.«Антонио Вивальди – итальянский композитор».

5.«Марс и Венера – планеты Солнечной системы».

6.10 < 9 + 1 тогда и только тогда, когда 9 < 8 + 1.

7.«Христофор Колумб открыл Америку или Африку».

8.Если – 3 < – 1, то 32 = 6.

9.15 делится на 5 и на 2.

Решение. Высказываниями являются предложения 1, 4, 5, 6, 7, 8, 9. Простыми высказываниями являются 1, 4. Высказывание 1 ложно,

высказывание 4 истинно.

Высказывания 5, 9 – конъюнкция, высказывание 7 – дизъюнкция. Конъюнкция 5 – истина, так как истинны высказывания «Марс –

планета Солнечной системы» и «Венера – планета Солнечной системы». Конъюнкция 9 ложна, так как высказывание «15 делится на 5» истинно, а высказывание «15 делится на 2» – ложно. Дизъюнкция 7 истинна, так как высказывание «Христофор Колумб открыл Америку» истинно, а высказывание «Христофор Колумб открыл Африку» – ложно.

Отрицание первого высказывания: «8 833 882 + 332». Отрицание четвёртого высказывания: «Неверно, что Антонио Вивальди – итальянский композитор». Конъюнкция высказываний: «8 833 < 882 + 332 и Антонио Вивальди – итальянский композитор». Дизъюнкция высказываний: «8 833 < 882 + 332 или Антонио Вивальди – итальянский композитор».

51

Задача 3.3. Укажите, какие из следующих предложений являются высказываниями, установите истинность простых высказываний. В сложных высказываниях выделите конъюнкцию и дизъюнкцию, установите истинность. Возьмите первые два высказывания и сформулируйте отрицание, конъюнкцию и дизъюнкцию.

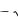
1. (4 7 ) 32.

2. «Множеством называют совокупность каких-либо объектов».

3. 72 49 и ( 7)2 49.

4.«Если 17 делится на 4, то 17 делится и на 2».

5.«Какой сегодня день?»

6.«Если кошки – хищники, то (– 1)2 = 1».

7.«Функция у = х2 – чётная или периодическая».

Задача 3.4. Какие из следующих высказываний истинны и какие ложны:

а) «Если число 18 делится на 7, то оно делится на 4»; б) «Если число 18 делится на 7, то оно делится на 6»; в) «Если число 18 делится на 6, то оно делится на 7»?

Задача 3.5. Истинно или ложно высказывание «15 = 2 ∙ 7→14 = 2 ∙ 7»? Задача 3.6. Истинно или ложно высказывание А, если известно, что

высказывание А → В ложно?

3.3 Формулы алгебры высказываний

Пусть Х, У, Z – переменные, вместо которых можно поставить любые элементарные высказывания (или их значения истинности). Такие переменные будем называть высказывательными (пропозиционными)

переменными. С помощью высказывательных переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить формулой, выражающей его логическую структуру. Например, высказывание «Если 100 делится на 2 и на 5, то 100 делится на 10» формализуется в виде ( Х У ) Z.

52

Формулой алгебры высказываний называется выражение,

составленное из высказывательных переменных с помощью операций над высказываниями и обращающееся в конкретное высказывание при подстановке вместо высказывательных переменных конкретных высказываний.

Формулой алгебры высказываний строятся следующим образом:

Подобно тому, как в арифметике установлена последовательность выполнения арифметических операций, в алгебре логики установлена своя последовательность выполнения операций:

1)операции в скобках;

2)операции отрицания. Если под знаком отрицания находится совокупность операций, например А В С , то вначале выполняются эти операции, потом их отрицание;

3)операция конъюнкции;

4)операция дизъюнкции;

5)операция импликации;

6)операция эквиваленции.

Пример 3.3. Запишите логической формулой следующее сложное высказывание: «Если социологические исследования показывают, что потребитель отдаёт предпочтение удобству и многообразию выбора, то фирме следует сделать упор на усовершенствование товара или увеличение многообразия новых форм».

Решение. Высказывание состоит из следующих простых:

А – «Социологические исследования показывают, что потребитель отдаёт предпочтение удобству»;

В – «Социологические исследования показывают, что потребитель отдаёт предпочтение многообразию выбора»;

С – «Фирме следует сделать упор на усовершенствование товара»;

53

D – «Фирме следует сделать упор на увеличение многообразия новых форм».

Логическая формула сложного высказывания: (А 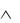В) → (С 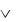D). Задача 3.7. Представьте логической формулой следующие сложные

высказывания:

1)«Если темпы роста рынка продукта корпорации высокие и размер контролируемой его доли рынка также высок, то в соответствии с матрицей портфельного анализа этот продукт относится к категории «звезда», он даёт большой доход, но требует значительных вложений»;

2)«Стратегическая хозяйственная единица корпорации занимает сильные позиции на рынке и работает в привлекательной отрасли. Следовательно, имеет наиболее высокий приоритет при распределении ресурсов»;

3)«Если прогноз показывает, что можно получить крупную прибыль на выпуске новых товаров, то при разработке стратегии развития фирме следует сделать упор на маркетинг и сеть распределения, а также целесообразно открыть более крупные магазины и расширить торговую сеть».

В логике изучается строение сложных логических высказываний, выраженных формулами, вне зависимости от содержания составляющих их простых высказываний.

Для того чтобы определить, какое значение принимает формула (истинное или ложное), составляют таблицу истинности.

Пример 3.4. Составьте таблицу истинности формулы алгебры

высказываний А В 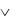А С В .

Решение. Для составления таблицы истинности данной формулы алгебры высказываний определим число исходных простых высказываний. Это высказывания А, В, С. Их число определяет число всевозможных

различных значений истинности А, В, С 23 8, то есть число строк таблицы.

54

В последнем столбце таблицы указаны значения истинности данной формулы алгебры высказываний.

Задача 3.8. Составьте таблицу истинности формулы алгебры высказываний.

55

Формула алгебры высказываний А, принимающая значение «истина» при любых возможных истинностных значениях, приписываемых её простым компонентам, называется тождественно истинной или законом логики, или тавтологией, или общезначимой. |=А читается: А тавтология

(общезначима). Например ( А В) (В С) ( А С) .

Формула алгебры высказываний, принимающая значение «ложь» при любых возможных истинностных значениях, приписываемых её простым компонентам, называется тождественно ложной или противоречием. Например А А .

Формула алгебры высказываний принимающая значение «истина» хотя бы при некоторых возможных истинностных значениях, приписываемых её простым компонентам, называется выполнимой.

Установить, является ли формула общезначимой, противоречивой или же выполнимой, но не общезначимой, можно, рассмотрев её таблицу истинности.

Пример 3.5. Является ли тавтологией формула алгебры высказываний

АВ В А ?

Решение. Формула алгебры высказываний является тавтологией, если её значения являются всегда истинными при всевозможных значениях истинности исходных простых высказываний, то есть в

56

последнем столбце таблицы истинности данной формулы должны стоять только единицы.

Составим таблицу истинности данной формулы.

57

3.4 Эквивалентные преобразования

Две формулы алгебры логики называются эквивалентными (равносильными), если они имеют одинаковые значения истинности при одинаковых истинностных значениях, приписываемых их простым компонентам. Эквивалентность обозначается знаком .

Алгебра логики обладает законами, называемыми основными эквивалентностями, позволяющими упрощать формулы алгебры логики и приводить их к виду, удобному для решения поставленных задач.

Основные эквивалентности:

1.А А (правило снятия двойного отрицания);

58

(дистрибутивность) конъюнкции относительно дизъюнкции); 13. А (В С) (А В) (А С) (распределительный закон (дистрибутивность) дизъюнкции относительно конъюнкции);

Правила операций с константами:

20.А 1 А;

21.А 1 1;

22.А 0 0 ;