
5543
.pdf
R(x, r) : " x 1 r";
S (a, b, c) : "а нравится b больше, чем с”. Запишите следующие высказывания:
а) Р(3, 4, 5); б) Q(8, 2); в) R(3, 7);
г) S(Джон, Сью, Мэри). Задача 4.2. Заданы предикаты:
P(x, y, z) : "x2 y2 z2";
Q(x, y) : "если y x2 , то х у";
R(a, b, x) : "a x2 b";
S (a, b) : " а играет в теннис лучше, чем b”. Запишите следующие высказывания:
а) Р(3, 4, 5); б) Q(– 2, 2); в) R(0, 4, – 3);
г) S(Джон, Фред).
Над предикатами можно проделывать те же самые логические операции, что и над высказываниями: отрицание, конъюнкцию, дизъюнкцию, импликацию, эквивалентность.
Отрицание. Пусть n-местный предикат Р(х1, х2, ..., хn) определён на
множествах М1, М2, ..., |
Мn. |
|
|
определяется |
как такой |
||
P(x1, x2, ..., xn ) |
|||||||
предикат, |
определённый на М1, М2, ..., Мn, что для любых |
предметов |
|||||
|
|
|
|
|
|
||
a1 M1 , |
a2 M 2 , ..., an |
M n |
высказывание |
P(a1, a2, ..., an ) является |
|||
отрицанием высказывания Р(а1, а2, ..., аn).
Конъюнкция. Пусть n-местный предикат Р(х1, х2, ... , хn) определён на
множествах М1, М2, ... , |
Мn и |
m-местный предикат Q(y1, y2, ... , ym) |
определен на множествах |
N1, N2, |
... , Nm. Р(х1, х2, ... , хn) Q(y1, y2, ... , ym) |
определяется как такой (n + m)-местный предикат, определённый на множествах М1, М2, ... , Мn, N1, N2, ... , Nm, что для любых предметов a1 M1 , a2 M 2 , ..., an M n и b1 N1, b2 N2 , ..., bm N m
81

высказывание Р(а1, а2, ... , аn) 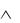 Q(b1, b2, ... , bm) является конъюнкцией высказываний Р(а1, а2, ... , аn) и Q(b1, b2, ... , bm).
Q(b1, b2, ... , bm) является конъюнкцией высказываний Р(а1, а2, ... , аn) и Q(b1, b2, ... , bm).
Аналогично определяются дизъюнкция, импликация и эквивалентность двух предикатов.
Задача 4.3. Даны предикаты:
Р(х): «Число х делится на 3» и Q(x): «Сумма цифр числа х делится на 9». Установите, какие из следующих импликаций истинны для всех натуральных чисел:
а) Р(х) 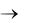
б) Q(х) 
в) Р (х) Q(x);
г) Q(х) P (x).
Задача 4.4. Выясните, являются ли следующие переменные высказывания равносильными, если x R :
а) |
x |
0, |
x2 |
0; |
|||
б) |
x |
x, |
|
x2 |
x; |
||
|
x |
||||||
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
x |
2, |
x |
2; |
||||
г) |
|
|
|
|
|
||
x |
2, |
x |
2. |
||||
4.2 Кванторы
Для ограничения области определения предметных переменных введём ещё одно логическое понятие, называемое квантором. Роль его выясним на следующих примерах:
1.«Все люди смертны. Сократ человек. Следовательно, Сократ смертен».
2.«Некоторые люди гениальны. Сократ человек, следовательно, Сократ гениален».
Во втором примере чувствуется ложность заключения, поскольку Сократ мог и не попасть в число гениальных людей.
82

Итак, ключевым |
словом |
в наших примерах является |
«все» и |
|
«некоторые». |
|
|
|
|
Термин «все х» обозначается в логике предикатов |
x и называется |
|||
квантором общности |
(символ |
есть перевёрнутая |
буква А, |
которая |
является начальной буквой английского слова All – «все»). Предикат записывают после квантора всеобщности ( x)P(x) . На естественном языке эта формальная запись означает: «для всех х значение Р(х) истинно».
Термин «некоторые х» или «существует хотя бы одно значение х» обозначается через x и называется квантором существования (символ 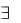 есть перевёрнутая буква Е, являющаяся первой буквой английского слова Exist – «существовать»). Предикат записывают после квантора существования ( x)P(x) . На естественном языке эта запись означает: «существуют такие элементы х, что Р(х) истинно».
есть перевёрнутая буква Е, являющаяся первой буквой английского слова Exist – «существовать»). Предикат записывают после квантора существования ( x)P(x) . На естественном языке эта запись означает: «существуют такие элементы х, что Р(х) истинно».
Переход от Р(х) к ( x)P(x) или ( x)P(x) называется связыванием переменной х, или навешиванием квантора на переменную х (или на предикат Р), или квантификацией переменной х.
Переменная, на которую навешен квантор, называется связанной, несвязанная квантором переменная называется свободной.
Выражение, на которое навешивается квантор ( x) или ( x) , называется областью действия квантора; все вхождения переменной х в это выражение являются связанными.
Навешивать кванторы можно и на многоместные предикаты и вообще на любые логические выражения.
Существуют предикаты, для которых область определения по различным предметным переменным ограничивают различными кванторами.
Например,
( x)( y)P(x, y) : «Для всех целых чисел х существует меньшее число у».
( x)( y)( z) P(x, y, z) : «Для всех целых чисел х и у существует число z, которое является частным от деления х на у».
83

Применение кванторов превращает одноместные предикаты в высказывания. Если имеется какой-либо k-местный предикат Р(х1, х2, ..., хk)
и |
применить |
квантор по какой-либо переменной, например |
( |
x1) P(x1, x2 , ..., |
xk ) , в результате получится (k – 1)-местный предикат. |
|
Пример 4.2. Пусть Р(х) – предикат «х – чётное число», определённый |
|
на множестве М. Дать словесную формулировку высказыванию ( x) P(x) , определить его истинность.
Решение. Исходный предикат Р(х): «х – чётное число» является переменным высказыванием: при подстановке конкретного числа вместо переменной х он превращается в высказывание, являющееся истинным или ложным, например, при подстановке числа 5 превращается в высказывание «5 – чётное число», являющееся ложным. Высказывание ( x) P(x) означает «В М существует чётное число». Поскольку множество М, на котором задан предикат Р(х), не определено в условии (в таком случае говорят, что задача сформулирована не вполне корректно), доопределим М.
Пусть предикат Р(х) определён на множестве натуральных чисел N, т.е. x N , тогда высказывание ( x) P(x) – истинно. В общем случае высказывание ( x) P(x) истинно на любом множестве М, содержащем хотя бы одно чётное число, и ложно на любом множестве нечётных чисел.
Пример 4.3. Пусть N(x) – предикат «х – натуральное число». Рассмотреть варианты навешивания кванторов. Дать словесную формулировку высказываниям и определить их истинность.
Решение. ( x) N (x) – высказывание «Все числа – натуральные» истинно на любом множестве натуральных чисел и ложно, если М содержит хотя бы одно ненатуральное число, например, целое отрицательное.
( x) N(x) – высказывание «Существует натуральное х» истинно на любом множестве М, содержащем хотя бы одно натуральное число, и ложно – в противном случае.
Пример 4.4. Рассмотреть все возможные варианты навешивания кванторов на предикат D(x,y): «х делится на у», определённый на множестве натуральных чисел (без нуля) N. Дать словесные формулировки полученных высказываний и определить их истинность.
84

Решение. Операции навешивания кванторов приводят к следующим формулам:
( x) D(x, y) – одноместный предикат (переменное высказывание) «всякое натуральное число из N делится на натуральное число y из N»; истинный только для одного значения свободной переменной y = 1;
( x) D(x, y) – переменное высказывание «Существует натуральное число, которое делится на у», истинное для любого значения свободной переменной у, взятой из множества N;
( y) D(x, y) – переменное высказывание «Натуральное число х делится на всякое натуральное число у», ложное для любого значения свободной переменной x, взятой из множества N;
( у) D(x, y) – переменное высказывание «Существует натуральное число, которое делит натуральное число х», истинное для любого значения свободной переменной;
( х)( у)D(x, y) ; ( y)( x)D(x, y) – высказывания «Для любых двух натуральных чисел имеет место делимость одного на другое», ложные;
( х)( у)D(x, y) ; ( y)( x)D(x, y) – высказывания «Существуют такие два натуральных числа, что первое делится на второе», истинны;
( х)( у)D(x, y) – высказывание «Существует натуральное число, которое делится на любое натуральное», ложное;
( y)( x)D(x, y) – высказывание «Для всякого натурального числа найдётся такое натуральное, которое делится на первое», истинное;
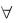
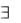 – высказывание «Для всякого натурального существует такое натуральное число, на которое оно делится», истинное;
– высказывание «Для всякого натурального существует такое натуральное число, на которое оно делится», истинное;
( у)( х)D(x, y) – высказывание «Существует натуральное число, которое является делителем всякого натурального числа», истинное (таким делителем является единица).
Рассмотрим примеры перевода в символическую форму. Предположение «Всякое рациональное число есть действительное
число», обозначая через Q(x): «х есть рациональное число», а через R(x): «х есть действительное число», мы можем выразить в символической форме в виде
( x) (Q(x) R(x)),
85

которая типична для высказываний вида «Всякое то-то есть то-то». Это просто значит то же, что Q R .
Подобным образом предложение «Некоторые действительные числа являются рациональными» можно перевести в символическую форму следующим образом:
( x) (R(x) Q(x)),
которая типична для высказываний вида «Некоторые то-то суть то-то». Смысл этого предложения сводится просто к тому, что R Q – непустое множество.
Отрицание утверждения типа «для всех» есть утверждение типа «для некоторого», а отрицание утверждение «для некоторого» есть утверждение типа «для всех». Традиционная логика особое внимание обращала на четыре основных типа высказываний:
отрицание утверждения «Все рациональные числа действительные»
есть утверждение «Некоторые рациональные числа не являются
действительными», а отрицание утверждения
«Некоторые рациональные числа действительны» есть утверждение
«Ни одно рациональное число не является действительным»
Задача 4.5. Используя высказывания:
а) ( x)( y) P(x, y, 25);
б) ( x) Q(x, 7);
в) ( r)( x) R(x, r);
г) ( c) S (Джон, Сью, с). Задача 4.6. Используя P,
высказывания:
86

а) ( x)( y)( z) P(x, y, z);
б) ( x)( y) Q(x, y);
в) ( x)( a)( b) R(a, b, x);
г) a S (а, Тед.).
Задача 4.7. Какой из кванторов определяется следующими выражениями: «Для всякого х истинно F(x)»; «F(x) при произвольном х»; «Найдётся х, такой что F(x)»; «Для подходящего х верно F(x)»; «Всегда имеет место F(x)»; «Каждый элемент обладает свойством F»; «Найдётся, по крайней мере, один х такой, что F(x)»; «Существует не менее одного х, что F(x)»; «Свойство F присуще всем»; «каким бы ни был х, F(x) истинно»; «Хотя бы для одного х верно F(x)».
Задача 4.8. Пусть Р(x): «х – простое число», Е(x): «x – чётное число» и D(x): «у делится на х». Перевести на русский язык:
1) Р(7); |
2) Е(2) Р(2); |
|
3) ( x)(D(2, x) E(x)); |
|||
|
|
|
|
|
|
|
4) ( x)(E(x) D(x, 6)); |
5) ( x)( E(x) D(2, |
x)). |
||||
Задача 4.9. Пусть Q(x, y) – предикат порядка «х ≤ у», определённый на |
||||||
конечном множестве натуральных чисел М |
0, 1, 2, 3, ..., 9 . Рассмотрите |
|||||
различные варианты квантификации его переменных. Определите истинность получаемых выражений.
Задача 4.10. Рассмотрите варианты навешивания кванторов на предикат Р(х, у), опишите в словесной форме полученные высказывания и определить их истинность, если:
1.Р(х, у), определённый на конечном множестве натуральных чисел, означает:
а) «х делит у» (или, что то же, «х является делителем у»); б) «х, у делятся на 3»;
в) «х ≥ у».
2.Р(х, у), определённый на множестве людей, означает:
а) «х является родителем у»; б) «х живёт в одном городе с у»; в) «х является сыном у».
Задача 4.11. Запишите приведённые ниже утверждения в
87

символической форме, введя предикаты. В случае необходимости укажите предметную область.
1.На каждой улице будет праздник.
2.Некоторые машины умнее людей.
3.Любой играет в теннис лучше Фреда.
4.Некоторые композиторы пишут симфонии лучше, чем другие.
5.Не существует совершенных героев.
6.Все студенты учатся усердно.
7.Некоторые целые числа делятся на 5.
4.3 Формулы логики предикатов. Выполнимость и истинность
Примеры и упражнения предыдущего параграфа служат для обоснования утверждения, что обычный язык можно в значительной мере символизировать точным образом, если дополнить логические связки предикатами и кванторами.
Формулы логики предикатов вводятся аналогично понятию формулы алгебры высказываний.
В дальнейшем будем называть прописные буквы латинского алфавита F, G, H, P, Q, … – нульместными предикатными переменными; F(,…,), G(,…,), H(,…,), P(,…,), Q(,…,), с указанием числа свободных мест в них – n- местными (n ≥ 1) предикатными переменными. Тогда
1)каждая нульместная предикатная переменная есть формула;
2)если P(,…,) – n-местная предикатная переменная, то Р(х1, ..., хn) есть формула, в которой все предметные переменные х1, ..., хn свободны;
3)Если F – формула, то F – также формула. Свободные (связанные)
предметные переменные в формуле F те и только те, которые являются свободными (связанными) в F;
4)если F1, F2 – формулы и если предметные переменные, входящие одновременно в обе эти формулы, свободные в каждой из них, то
выражения (F1 F2 ) , (F1 F2 ) , (F1 F2 ) , (F1 F2 ) также являются формулами. При этом предметные переменные, свободные (связанные) хотя
88

бы в одной из формул F1, F2, называются свободными (связанными) и в новых формулах;
5) если F – формула и х предметная переменная, входящая в F свободно, то выражения ( x)F и ( x)F также являются формулами, в которых переменная х связанная, а все остальные предметные переменные, входящие в формулу F свободно или связанно, остаются и в новых формулах соответственно такими же;
6) никаких других формул логики предикатов нет.
Формулы, определённые в п.1 и 2, называются элементарными (или атомарными). Формулы, не являющиеся элементарными, называются составными.
Например, |
P, Q(x, |
y, z), R(x1, x2 ) – элементарные формулы, а |
( y)P(x, y, z), ( x)( |
y)Р(x, |
y, z) – составные формулы. |
Формулы, в которых нет свободных предметных переменных, называются замкнутыми, а формулы, содержащие свободные предметные переменные – открытыми.
Превращение формулы логики предикатов в высказывание (а также само получаемое высказывание) называется интерпретацией этой формулы на множестве М:
–если формула логики предикатов замкнутая, то её интерпретация сводится к подстановке вместо всех предикатных переменных конкретных предикатов, определённых на множестве М, в результате чего формула превращается в конкретное высказывание;
–если формула логики предикатов открытая, то её интерпретация состоит из двух этапов:
1)вместо всех предикатных переменных подставляем конкретные предикаты, определённые на множестве М, в результате чего формула превратится в конкретный предикат, зависящий от такого количества предметных переменных, сколько было свободных предметных переменных
висходной формуле;
2)подставляем вместо этих предметных переменных конкретные предметы из множества М, в результате чего этот предикат (и, значит, вся исходная формула) превратится в конкретное высказывание.
89

Пример 4.5. Дадим интерпретацию формуле ( х) ( у) Р(х, у) . Решение. В качестве множества М возьмём множество всех мужчин, а
вместо предикатной переменной Р(х, у) подставим конкретный предикат, определённый на М: «х есть отец у». Тогда исходная формула превратится в следующее ложное высказывание ( х) ( у) (х есть отец у) – «У каждого мужчины есть сын».
Этой же формуле можно дать и другую интерпретацию. Возьмём в качестве множеств М множество N всех натуральных чисел, а вместо предикатной переменной Р(х, у) подставим конкретный предикат «x < y», определённый на N2. Тогда исходная формула превратится в истинное высказывание ( х) ( у) (x y) – «Для каждого натурального числа существует большее по сравнению с ним натуральное число».
Формула логики предикатов называется выполнимой (опровержимой) на множестве М, если при некоторой подстановке вместо предикатных переменных конкретных предикатов, заданных на этом множестве, она превращается в выполнимый (опровержимый) предикат.
Другими словами, формула выполнима (опровержима) на М, если существует истинная (ложная) её интерпретация на М.
Формула логики предикатов называется тождественно истинной (тождественно ложной) на множестве М, если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на этом множестве, она превращается в тождественно истинный (тождественно ложный) предикат.
Формула логики предикатов называется общезначимой, или
тавтологией (тождественно ложной или противоречием), если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах, она превращается в тождественно истинный (тождественно ложный) предикат.
Тот факт, что формула F является тавтологией, обозначается, как и в алгебре высказываний, ╞ F.
Пример 4.6. Показать, что формула Р(х) ( у) Р( у) является противоречием (тождественно ложной).
90
