
5543
.pdf
Решение. Допустим противное: на некотором множестве М имеется конкретный предикат А(х), такой, что данная формула превращается в
|
|
|
|
|
|
|
|
выполнимый предикат (от х) |
А(х) ( у) А( у) . |
|
|
|
|||
Последнее |
означает: |
найдётся предмет |
a M , такой, что |
||||
|
|
|
|
|
|
||
высказывание А(a) |
( у) А( у) истинно. |
|
|
|
|||
|
|
|
|
|
|||
Истинность |
конъюнкции даёт истинность |
высказываний А(a) и |
|||||
( у) А( у) . Из истинности первого следует, что высказывание А(а) ложно, а из истинности второго – что предикат А(у) тождественно истинный и, значит, для любого предмета из М, в том числе и для a M , высказывание А(а) истинно. Получаем противоречие, исключающее предположение о непротиворечивости исходной формулы. Следовательно, она тождественно ложна.
Пример 4.7. Показать, что формула ( х) (Р(х) Р(х)) – тавтология. Решение. Допустим противное: на некотором множестве М имеется
конкретный предикат А(х), такой, что данная формула превращается в
|
|
|
|
|
|
опровержимый предикат ( х) (А(х) А(х)) . |
|||||
Последнее |
означает: найдётся предмет a M , такой, что |
||||
|
|
|
|
||
высказывание А(а) |
|
А(a) ложно. |
|||
Ложность дизъюнкции даёт ложность высказываний А(а) и А(a) . Из ложности первого следует истинность второго, а из ложности второго – истинность первого. Получаем противоречие, исключающее предположение о необщезначимости исходной формулы. Следовательно, она тавтология.
Пример 4.8. Докажите, что формула ( х) (Р(х) Q(x) P(x)) является тавтологией.
Решение. Предположим противное: на некотором множестве М имеются конкретные предикаты А(х) и В(х), такие, что данная формула
превращается |
в опровержимый предикат |
( х) ( А(х) В(x) |
А(x)) . |
Последнее означает: найдётся предмет a |
M , такой, что высказывание |
||
А(а) В(а) |
А(а) ложно. Это возможно лишь тогда, когда А(а) |
≡ 0, а |
|
А(а) В(а) ≡ 1, но последнее требует, чтобы А(а) ≡ 1 и В(а) ≡ 1. Таким образом, требуется, чтобы существовала константа а в области М такая, что
91

А(а) ≡ 0 и А(а) ≡ 1, что невозможно. Следовательно, принятое
предположение неверно, и поэтому формула |
( |
х) (Р(х) |
Q(x) |
P(x)) – |
|
тавтология. |
|
|
|
|
|
Задача 4.12. Покажите, что формула |
|
|
|
|
является |
( |
х) (Р(х) |
Р(х)) |
|||
противоречием.
Задача 4.13. Докажите методом от противного, что следующие формулы являются тавтологиями:
1) |
( х)((Р(х) |
Q(x)) (Q(x) P(x))) ; |
||
2) |
( х) ( (Р(х) |
Q(x)) |
(Р(x) |
Q(x))); |
3) |
( х) ( Р(х) |
(Q(x) |
(Р(x) |
Q(x)))). |
Нахождение тавтологий является одной из важнейших задач логики предикатов, как и алгебры высказываний. При установлении общезначимости формулы таблицы истинности должны уступить место процессам рассуждения, так как значение предиката зависит от выбора значений его предметных переменных, который, вообще говоря, можно сделать бесконечным числом способов.
Рассмотрим наиболее важные тавтологии логики предикатов (ниже Р
– любая формула, не содержащая х).
Законы коммутативности для кванторов
1. ╞ ( |
х) ( у) |
Р(х, |
у) |
( |
|
|
у) ( х) Р(х, у) |
(4.1) |
|||||||||
╞ ( х) ( у) |
Р(х, |
у) |
( |
|
у) ( х) Р(х, у) |
(4.2) |
|||||||||||
2. ╞ ( |
х) ( у) |
Р(х, |
у) |
( |
|
|
у) ( х) Р(х, у) |
(4.3) |
|||||||||
|
|
|
|
|
Выражения кванторов одного через другой |
|
|||||||||||
3. ╞ ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.4) |
|||
х) Р(х) |
( х) Р(х) |
|
|||||||||||||||
╞ ( |
|
|
|
|
|
|
|
|
|
(4.5) |
|||||||
х) Р(х) |
( х) Р(х) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Правила переноса через кванторы |
|
||||||
4. ╞ ( |
|
|
|
|
|
|
|
(4.6) |
|||||||||
х) Р(х) |
( х) Р(х) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
╞ ( |
х) Р(х) |
( |
|
х) Р(х) |
|
(4.7) |
|||||||||||
92

Законы перенесения кванторов через конъюнкцию и дизъюнкцию
5. ╞ ( |
х) (Р(х) |
Q(х)) |
( х) Р(х) |
( х) Q(х) |
(4.8) |
||
╞ ( |
х) (Р(х) |
Q(х)) |
( |
х) Р(х) |
( х) Q(х) |
(4.9) |
|
6. ╞ ( |
х) Р(х) |
|
( x) Q(х) |
( х) (Р(х) Q(х)) |
(4.10) |
||
╞ ( |
х) (Р(х) |
Q(х)) |
( |
х) Р(х) |
( x) Q(х) |
(4.11) |
|
7. ╞ ( |
х) (Р |
Q(х)) |
Р |
( x) Q(х) |
|
(4.12) |
|
╞ ( |
х) (Р |
Q(х)) |
Р |
( x) Q(х) |
|
(4.13) |
|
8. ╞ ( |
х) (Р |
Q(х)) |
Р |
( х) Q(х) |
|
(4.14) |
|
╞ ( |
х) (Р Q(х)) |
P |
( х) Q(х) |
|
(4.15) |
||
4.4 Эквивалентные соотношения. Префиксная нормальная форма
Две формулы, F и Н логики предикатов называются эквивалентными (равносильными) на множестве М, если при любой подстановке в эти формулы вместо предикатных переменных любых конкретных предикатов, определённых на М, формулы превращаются в эквивалентные предикаты. Если две формулы эквивалентны на любых множествах, то их будем называть просто эквивалентными (равносильными). Эквивалентность будем обозначать так: F ≡ H.
В логике предикатов эквивалентные соотношения позволяют выполнять корректные преобразования предикатных формул. Переход от одной эквивалентной формулы к другой называется эквивалентным (равносильным) преобразованием исходной формулы. В логике предикатов справедливы все эквивалентные соотношения логики высказываний, а также собственные эквивалентные соотношения, включающие связки и .
Формулы F и Н эквивалентны (F ≡ H) тогда и только тогда, когда формула F ↔ H является тавтологией (╞ F ↔ H).
Это замечание вместе с (4.1) – (4.15) позволяет указать наиболее важные примеры эквивалентных формул (ниже под Р будем понимать переменное высказывание или формулу, не содержащую х):
93

|
|
|
|
|
|
|
|
|
|
(4.16) |
|
|
( |
x) P(x) |
( x) P(x) |
|
|
||||||
|
|
|
|
|
|
|
|
|
(4.17) |
||
( |
x) P(x) |
( x) P(x) |
|
|
|||||||
( |
x) (P(x) |
Q(x)) |
( x) P(x) |
( x) Q(x) |
(4.18) |
||||||
( |
x) (P(x) |
Q(x)) |
( x) P(x) |
( x) Q(x) |
(4.19) |
||||||
( |
x)( y) P(x, y) |
( y)( x) P(x, y) |
(4.20) |
||||||||
( |
x)( y) P(x, y) |
( |
y)( x) P(x, y) |
(4.21) |
|||||||
( |
x) (P(x) |
P) |
( |
x) P(x) |
P |
|
(4.22) |
||||
( |
x) (P(x) |
P) |
( |
x) P(x) |
P |
|
(4.23) |
||||
( |
x) (P(x) |
P) |
( |
x) P(x) |
P |
|
(4.24) |
||||
( |
x) (P(x) |
P) |
( |
x) P(x) P |
|
(4.25) |
|||||
|
|
|
|
Соотношения (4.18) и (4.19) показывают дистрибутивность квантора |
|||||||
общности |
( x) |
относительно конъюнкции и квантора существования ( x) |
|||||||||
относительно дизъюнкции. Если в этих выражениях поменять местами
кванторы ( x) и ( |
x) , то получим соотношения, верные лишь в одну сторону: |
|
( |
x) (P(x) |
Q(x)) ( x) P(x) ( x) Q(x) ; |
( |
x) (P(x) |
( x) Q(x) ( x) (P(x) Q(x)) . |
Поэтому в таких случаях эквивалентных преобразований применяют переименование переменной х в одном из предикатов на новую переменную:
( |
x) P(x) |
( у) Q( у) ( x)( у) (Р(x) |
Q( у)) ; |
( |
x) P(x) |
( у) Q( у) ( x)( у) (P(x) |
Q( у)) . |
Для анализа сложных суждений рекомендуется формулы приводить к тому или иному более удобному виду. Один из таких видов носит название приведённой формы.
Приведённой формой для формулы логики предикатов называется такая эквивалентная ей формула, в которой из операций алгебры высказываний имеются только операции отрицания, конъюнкции и дизъюнкции, причём знаки отрицания относятся лишь к предикатным переменным и к высказываниям.
Ещё одним удобным видом формулы, к которому её можно привести эквивалентными преобразованиями, является префиксная нормальная форма.
94
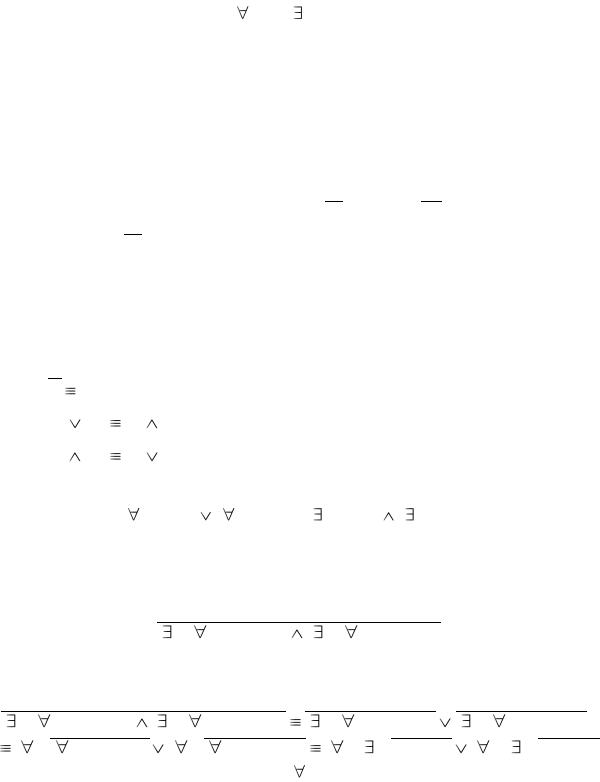
Префиксной нормальной формой (ПНФ) для формулы логики предикатов называется такая её приведённая форма, в которой все кванторы стоят в её начале, а область действия каждого из них распространяется до конца формулы, т.е. это формула вида
(k1x1) … (kmxm) (F(x1, …, xn)),
где ki есть один из кванторов или (i = 1, …, m), m ≤ n, причём формула F не содержит кванторов и является приведённой формулой (заметим, что кванторы в формуле могут отсутствовать вовсе).
Алгоритм приведения формулы к виду ПНФ
1.Исключите всюду логические связки ↔ и → по правилам:
F1 ↔ F2 ≡ (F1 → F2) 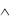 (F2 → F1) ≡ ( F1
(F2 → F1) ≡ ( F1  F2)
F2)  ( F2
( F2  F1); F1 ↔ F2 ≡ F1
F1); F1 ↔ F2 ≡ F1 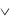 F2.
F2.
2.Представьте предикатную формулу таким образом, чтобы
символы отрицания были расположены непосредственно над символами предикатов, воспользовавшись правилами (4.16) – (4.17), а также правилом:
F |
F; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
F2 |
F1 |
F2; |
|||||
|
|
|
|
|
|
|
||
F1 |
F2 |
F1 |
F2. |
|||||
3. Для формул, содержащих подформулы вида
( x)F1(x) ( x)F2 (x), ( x)F1(x) ( x)F2 (x),
ввести новые переменные, позволяющие использовать соотношения (4.22) – (4.25). 4. С помощью формул (4.18) – (4.25) получить формулы в виде ПНФ. Пример 4.9. Привести к ПНФ следующую предикатную формулу:
( x)( y) F1(x, y) ( x)( y) F2 (x, y).
Решение. Переместим символ отрицания непосредственно к символам предикатов:
( x)( y) F1(x, y) ( x)( y) F2 (x, y) ( x)( y) F1(x, y) ( x)( y) F2(x, y) 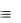 ( x)( y) F1(x, y) ( x)( y) F2(x, y) ( x)( y)F1(x, y) ( x)( y)F2 (x, y).
( x)( y) F1(x, y) ( x)( y) F2(x, y) ( x)( y)F1(x, y) ( x)( y)F2 (x, y).
Так как квантор общности ( x) не дистрибутивен относительно
95

дизъюнкции, поменяем в каком-либо предикате, например во втором, переменную х на новую переменную z:
( x)( y) F1(x, y) ( x)( y) F2(x, y) ( x)( y) F1(x, y) ( z)( y) F2(z, y).
Окончательно получим префиксную нормальную форму для исходной предикатной формулы:
( x)( y) F1(x, y) ( z)( y) F2 (x, y) ( x)( z)(( y) F1(x, y) ( y) F2(z, y)) 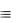
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x)( z)( y) (F1 (x, y) |
|
|
F2 (z, y)). |
|
|
|
||||||
Правило перемещения символа отрицания слева направо для |
||||||||||||||||
многоместных предикатов, например, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P |
|
|
P |
|
P |
|
P |
P |
P. |
||||||
Таким образом, чтобы произвести полное отрицание многоместного предиката с кванторами, необходимо прибегнуть к замене: 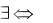 , P P .
, P P .
Пример 4.10. Получить ПНФ предикатной формулы:
( x)( y)(( z)(F1(x, z) |
F2 ( y, z)) |
( u) F3 (x, y, u)). |
||||||||
Решение. ( x)( y)(( z)(F1 (x, z) |
F2 ( y, z)) |
( u) F3 (x, y, u)) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
( x)( y) (( z) (F1(x, z) |
F2( y, z)) |
( u) F3(x, y, u)) |
||||||||
|
|
|
|
|
|
|
|
|||
( x)( y) (( z) F1(x, z) |
|
F2 ( y, z) ( u) F3(x, y,u)) |
||||||||
|
|
|
|
|
|
|
|
|||
( x)( y) (( z) F1(x, z) |
F2(y, z)) ( u) F3(x, y,u)) |
|||||||||
|
|
|
|
|
|
|||||
( x)( y) ( z)( F1(x, z) |
|
F2 ( y, z) ( u) F3(x, y,u)) |
||||||||
( x)( y)( z)( u)( F1(x, z) F2 ( y, z) F3(x, y,u)).
Пример 4.11. Получить ПНФ предикатной формулы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(( u) F1(u) |
|
( y)( u) F2 ( y, u)) |
( x) F3(x). |
||||||||||
Решение. Для получения ПНФ осуществим эквивалентные |
|||||||||||||
преобразования: |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
(( u) F1(u) |
( y)( u) F2 ( y, u)) |
( x) F3(x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
(( u) F1 (u) ( y)( u) F2 ( y, u)) |
( x) F3 (x) |
||||||||||
|
|
|
|
|
|||||||||
|
(( u) F1(u) ( y)( u) F2 ( y, u)) |
( x) F3(x) |
|||||||||||
( u) F1(u) ( y)( u) F2 ( y, u) ( x) F3(x) 
( u) F1 (u) ( y)( u) F2 ( y, u) ( x) F3 (x) 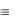
( u) F1(u) ( y)( u) F2 ( y, u) ( x) F3(x) 
96
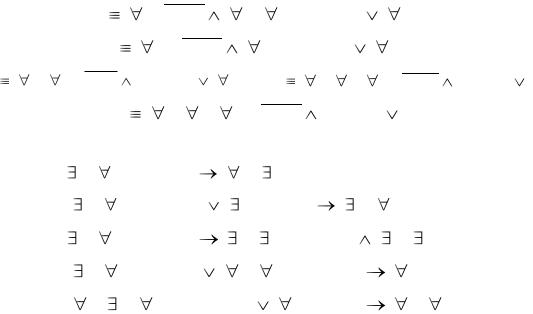
( u) F1(u) ( y)( u) F2( y, u) ( x) F3(x) 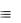 ( u) (F1(u) ( y) F2( y, u)) ( x) F3(x)
( u) (F1(u) ( y) F2( y, u)) ( x) F3(x) 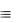
( u)( y) (F1 (u) F2 ( y, u)) ( x) F3 (x) ( u)( y)( x) (F1(u) F2( y, u) F3(x)) 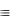
( x)( y)( u) (F1(u) F2 ( y, u) F3(x)).
Задача 4.14. Получить ПНФ следующих предикатных формул:
1) ( x)( y) F1(x, y) |
( x)( y) F2 (x, y); |
|
|
|
|
||||||
2) (( x)( y) F2 (x, y) |
( x) F2 (x)) ( y)( z) F3 ( y, z); |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3) ( x)( y) F1(x, y) |
( y)( z) F2 ( y, z) ( y)( z) F3( y, z); |
||||||||||
|
|
|
|
|
|
|
|
||||
4) (( x)( y) F1(x, z) ( x)( y) F2(x, y)) |
( z) F3(z); |
||||||||||
|
|
|
|
|
|
||||||
5) (( x)( y)( z) F1(x, y, z) ( y) F2( y)) |
( x)( z) F3(x, z). |
||||||||||
Глава 5. ТЕОРИЯ ГРАФОВ
Теория графов находит самое широкое применение в моделировании информационных процессов, в программировании и в решении экономических задач. Она позволяет просто описывать сложные явления и даёт им графическую интерпретацию.
Первая работа по теории графов была опубликована математиком Л. Эйлером в 1736 г. в Трудах Академии наук Санкт-Петербурга в виде задачи о Кёнигсбергских мостах (рисунок 5.1). Суть задачи сводилась к следующему: мог ли житель Кенигсберга, выйдя из дома, находящегося на части суши A, B, С или D, пройти по семи мостам через реку Прегель в точности по одному разу и вернуться домой? Ответ на этот вопрос был отрицательным.
97
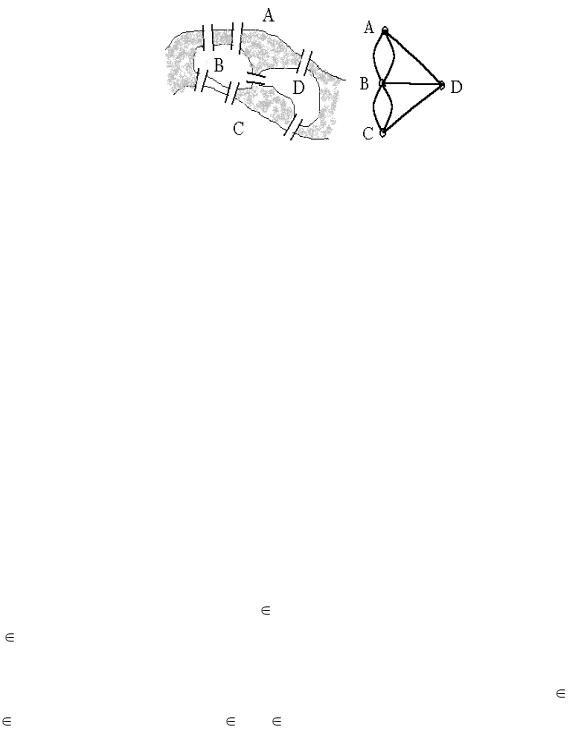
Рисунок 5.1 – Кёнигсбергские мосты и их модель
Для пояснения задачи представлена модель (рисунок 5.1), где каждый участок суши замещён точкой на плоскости, а мосты – линиями, связывающими участки суши.
5.1 Основные понятия теории графов. Способы задания графов
Графические представления в узком смысле – это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий –
рёбер или дуг.
Графом G называется совокупность двух множеств: |
вершин V и |
рёбер E, между элементами которых определено |
отношение |
инцидентности – каждое ребро е E инцидентно ровно двум вершинам vi, vj V, которые оно соединяет. При этом вершина vi (vj) и ребро е называются инцидентными друг другу, а вершины vi и vj, являющиеся для ребра е концевыми точками, называются смежными. Часто вместо v V и е Е пишут соответственно v G, е G.
Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой; в этом случае оно называется направленным, или ориентированным, или дугой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом.
Граф, соединяющий направленные рёбра (дуги) с началом vi и концом vj, называется ориентированным (орграфом), а ненаправленные –
неориентированным (н-графом) (рисунок 5.2).
98

а) |
|
|
б) |
|
|
v1 |
е3 |
v3 |
v1 |
е3 |
v3 |
|
|
|
|
||
е1 |
е5 |
е6 |
е1 |
е5 |
е6 |
е4 |
|
е4 |
|
||
|
v5 |
|
|
||
v0 |
|
v0 |
|
|
|
е2 |
|
е8 |
е2 |
|
е8 |
|
|
|
|
||
v2 |
v4 |
|
v2 |
v4 |
|
|
|
|
|
Рисунок 5.2 – н-граф (а) и орграф (б)
Рёбра, инцидентные одной и той же паре вершин, называются параллельными, или кратными. Граф, содержащий кратные рёбра, именуется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлёй.
Граф называется конечным, если множество его элементов (вершин и рёбер) конечно, и пустым, если его множество вершин V (а значит и рёбер E) пусто. Граф без петель и кратных рёбер именуется полным, если каждая пара вершин соединена ребром.
Дополнением графа G называется граф G , имеющий те же вершины, что и граф G, и содержащий только те рёбра, которые нужно добавить к графу G, чтобы получить полный граф.
Локальной степенью (или просто степенью) вершины v V н-графа
G называется количество рёбер ρ(v), инцидентных вершине v. В н-графе сумма степеней всех вершин равна удвоенному числу рёбер m графа, т.е. чётна (предполагается, что в графе с петлями петля даёт вклад 2 в степень вершины):
(v) 2m ,
v G
отсюда следует, что в н-графе число вершин нечётной степени чётно.
Для вершины орграфа определяются две локальные степени:
99

ρ1(v) – число рёбер с началом в вершине v, или количество выходящих из v рёбер;
ρ2(v) – количество входящих в v рёбер, для которых эта вершина является концом.
Петля даёт вклад 1 в обе эти степени.
В орграфе суммы степеней всех вершин ρ1(v) и ρ2(v) равны количеству рёбер m этого графа, а значит, и равны между собой:
1(v) |
2 (v) m . |
v G |
v G |
Графы G1 и G2 равны, т.е. G1 = G2, если их множества вершин и рёбер (выраженных через пары инцидентных им вершин) совпадают:
V1 = V2 и Е1 = Е2.
Граф G считается полностью заданным в строгом смысле, если нумерация его вершин и рёбер зафиксирована. Графы, отличающиеся только нумерацией вершин и рёбер, называются изоморфными.
Пример 5.1. Задать граф G (рисунок 5.3) через множество вершин и рёбер.
v2 |
v1 |
е1 |
|
е4 |
|
е2 |
v3 |
v4 |
е3 |
|
|
v5 |
|
Рисунок 5.3 – Граф G
Решение. Граф G может быть полностью определён:
– двумя множествами поименованных вершин V1 = {v1, v2, v3, v4, v5} и поименованных рёбер Е1 = {e1, e2, e3, e4} (в строгом смысле требуется установление отношения инцидентности рёбер соответствующим вершинам);
100
