
5543
.pdf
F1 |
(F2 F3 ) (F1 |
F2 ) (F1 F3 ) . |
3. |
Удалить лишние |
конъюнкции и повторения переменных в |
конъюнкциях применяя закон:
F F F ;
F F F ;
F F 0;
FF 1.
4.Удалить константы с помощью правил операций с константами:
F1 F ;
F 1 1;
F 0 0 ;
F 0 F .
Пример 3.9. Приведите к ДНФ формулу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А В А (В А С) (А (В С) В С). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. А В А (В А С) |
(А (В С) В С) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(А В) (А В А А С) |
|
|
А (В С) В С |
|||||||||||||||
(А В) (А В) (А (В С)) В С (А В) (А В) (А В С) (В С) 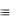
(А В) (А В) ((А В) (А С) (В В С) (В С С)) 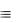 (А В) (А В) ((А В) (А С) (В С))
(А В) (А В) ((А В) (А С) (В С)) 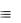
(А В) (А В) ((А В) (В С)) (А В) (А В С) 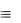
В (А (А С)) В (А С) (А В) (В С).
Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.
КНФ формулы есть формула, имеющая вид конъюнкции элементарных дизъюнкций, т.е.
F |
D1 D2 D3 |
... Dm , где Di |
( A B |
C ... D). |
|
В элементарной дизъюнкции нет двух одинаковых |
|||||
пропозициональных переменных, т.к. F |
F |
F , |
а в КНФ нет двух |
||
одинаковых |
элементарных |
дизъюнкций, т.к. |
F |
F F . Если одна из |
|
элементарных дизъюнкций содержит пропозициональную переменную и её отрицание F F , то следует удалить всю элементарную дизъюнкцию,
71
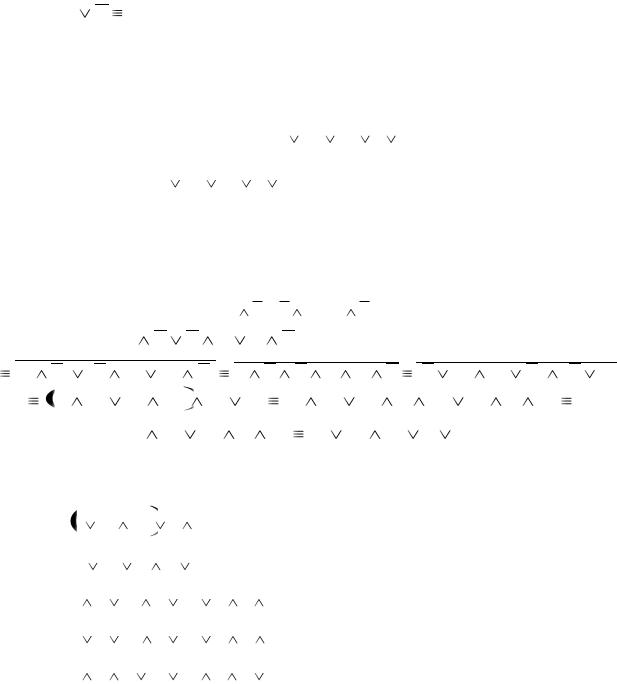
так как F F 1.
Процедура приведения ДНФ к КНФ:
1. Примените к F правило снятия двойного отрицания
|
|
|
|
|
F ≡ К1 |
К2 К3 ... Кm |
|
|
|
|
|
и приведите К1 К2 К3 ... Кm |
к ДНФ. |
||
2. С помощью закона де Моргана освободитесь от второго отрицания и преобразуйте отрицания элементарных конъюнкций в элементарные дизъюнкции.
Пример 3.10. Приведите к КНФ формулу:
А В 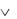 А В
А В 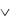 А С .
А С .
Решение. А В А В А С 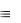
(А В) (А В) (А С) А В А В А С (А В) ( А В) (А С) 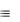
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(А В) (А В) |
|
|
(А С) (А В) (А В С) (А В А) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(А В) (А В С) (А В) (А В С). |
||||||||||||||||||||||||||||||||||||||||||||
Задача 3.16. Приведите к ДНФ и КНФ формулы: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C ; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
A |
|
|
(B |
|
|
|
|
C) |
|
|
A |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B ; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
( A |
|
|
|
B) |
|
|
|
|
|
|
A |
C |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
A B ( A C B) |
|
A B C ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
|
A B C ; |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
A C ( A B C) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) A B C (B A) |
|
A C B. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.8 Логическое следствие
Задача логики дать принцип рассуждения, то есть теорию вывода. Практически это сводится к получению критериев для решения механическим путём вопроса о том, можно ли некоторую цепь рассуждений, основываясь на её форме, считать правильной.
72

Мы знаем, например, что если истинно А, то, независимо от истинности
или ложности В, дизъюнкция А |
B истина. В этом случае говорят, что А B |
|||
логически следует из А. В случае, если истина конъюнкция А |
B , то истинно |
|||
и А. Говорят, что А логически следует из А B . |
|
|
||
Цепь |
рассуждений |
представляет |
собой |
конечную |
последовательность высказываний, проводимых в обоснование утверждения, при этом последнее высказывание в этой последовательности (заключение) может быть выведено из некоторых начальных высказываний (посылок).
Высказывание В (заключение) есть логическое следствие высказываний А1 , А2 ,..., Аm (посылок):
А1, А2 ,..., Аm B ,
если из конъюнкции посылок следует заключение, то есть всегда, когда
посылки истины, заключение тоже истинно. |
|
|
|
||
Теорема 1 (связь между импликацией и логическим следствием). |
|
||||
(I) |
А |
B тогда и только тогда, когда |= А |
B . |
|
|
(II) |
А1, А2 ,..., Аm B тогда и только тогда, когда |= А1 |
А2 ... Аm |
B . |
||
Можно |
представить доказательство |
того, что |
формула |
В |
|
(заключение) |
есть логическое следствие формул А1 , А2 ,..., Аm |
(посылок), в |
|||
виде цепочки (т.е. конечной последовательности) формул, последней из которых является В, и притом такой цепочки, что наличие в ней каждой из формул Е обосновывается применением одного из следующих правил.
Правило р: формула Е есть посылка.
Правило t: формуле Е в цепочке предшествуют такие формулы А, …,
С, что |= А ... С Е . |
|
Иными словами, мы утверждаем, что А1 , А2 ,..., Аm |
B , если мы можем |
составить такую цепочку формул Е1, Е2 ,..., Еm (= B ), |
что каждая Е есть |
посылка (правило р) или же в этой цепочке есть предшествующие формулы такие, что если С – их конъюнкция, то С Е (правило t).
Приведём перечень некоторых тавтологических импликаций. То, что каждая из приведённых формул – тавтология, можно доказать, составив для неё таблицу истинности. Каждая из тавтологических импликаций порождает
73

некоторое правило вывода, а именно частный случай применения правила t, который обосновывается ссылкой только на одну эту тавтологию.
Тавтологические импликации: |
|
|
|
|
|
|
|
||||||||||||||||||||
1. |
|= А |
|
( А |
|
В) |
|
|
В правило отделения (modus ponens MP). |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. |
|= |
В |
|
( А |
|
В) |
|
|
А правило отрицания (modus tollens MT). |
||||||||||||||||||
3. |
|= |
|
|
|
|
|
|
В . |
|
|
|
|
|
|
|
|
|
|
|||||||||
А |
|
( А В) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4. |
|= |
А |
|
(В |
А |
В) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. |
|= |
А |
|
В |
А правило удаления конъюнкции. |
|
|
|
|
||||||||||||||||||
6. |
|= |
А |
|
|
А |
В правило введения дизъюнкции. |
|
|
|
|
|||||||||||||||||
7. |
|= ( А |
В) |
(В |
|
С) |
( А |
|
С) правило силлогизма. |
|
|
|
|
|||||||||||||||
8. |= ( А В С) |
|
( А (В С)) . |
|
|
|
|
|
|
|||||||||||||||||||
9. |
|= ( А |
(В |
|
С)) |
|
( А |
В |
|
С) правило соединения посылок. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10. |= ( А |
В |
В ) |
|
А . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
11. |= ( А |
В) |
|
|
( А |
|
С |
В |
С) . |
|
|
|
|
|
|
|
||||||||||||
12. |= ( А |
В) |
|
|
( А |
|
С |
В |
С) . |
|
|
|
|
|
|
|
||||||||||||
13. |= ( А |
В) |
((В |
С) |
|
( А С)) . |
|
|
|
|
|
|||||||||||||||||
14. |= ( А |
В) |
|
(В |
|
|
С) |
( А |
|
С) правило введения эквиваленции. |
||||||||||||||||||
Пример 3.11. Докажите, что А |
В, А |
С, В |
D C |
D . |
|||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(1) |
А |
|
|
|
С |
|
|
|
|
(р); |
|
|
|
|
|
|
|
|
|
|
|||||||
(2) |
А |
|
|
|
B |
С |
|
B |
(1t), |=(1) (2) на основании тавтологии 11; |
||||||||||||||||||
(3) |
В |
|
|
|
D |
|
|
|
|
(р); |
|
|
|
|
|
|
|
|
|
|
|||||||
(4) |
С |
|
|
|
В |
С |
|
D (3t), |=(3) |
|
(4) на основании тавтологии 11; |
|||||||||||||||||
(5) |
А |
|
|
|
B |
С |
|
D (2,4t), |=(2) |
|
(4) (5) на основании тавтологии 7; |
|||||||||||||||||
(6) |
А |
|
|
|
В |
|
|
|
|
(р); |
|
|
|
|
|
|
|
|
|
|
|||||||
(7) |
C |
|
|
|
D |
|
|
|
|
(5,6t), |=(5) |
|
(6) (7) на основании тавтологии 1. |
|||||||||||||||
Пример 3.12. Докажите, что А |
|
|
|
|
|
|
|
||||||||||||||||||||
В, В |
С, С |
D, Е |
D А Е . |
||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(р) |
|
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2) |
А |
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
(р) |
|
|
|
|
|
|
|
|
|
||
(3) |
В |
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
(р) |
|
|
|
|
|
|
|
|
|
||
74

(4) |
С |
D |
(р) |
||||
(5) |
А |
D |
(2,3,4t) |
||||
(6) |
|
|
|
|
|
|
(1t) |
D |
|
Е |
|||||
(7) |
|
|
|
|
(5,6t) |
||
А |
Е |
||||||
Задача 3.17. Постройте формальное доказательство логичности рассуждения.
Если человек занимается спортом, то он хочет быть здоровым. Хорошее здоровье ведёт к счастливой жизни. Кроме того, если человек занимается спортом, то он, как правило, стремится достичь высоких спортивных результатов. Наличие высоких результатов позволяет одержать победы на соревнованиях. Победы на соревнованиях влекут за собой всеобщее признание. Однако человек не хочет жить счастливо и иметь всеобщее признание. Значит, он не станет заниматься и спортом.
Правило |
ср (правило условного доказательства): |
формула В C |
оправдана в |
выводе, посылками которого служат |
А1 , А2 ,..., Аm , если |
установлено, что С есть логическое следствие формул А1 , А2 ,..., Аm и В. |
||
То есть |
А1 , А2 ,..., Аm В C тогда и только тогда, |
когда А1 , А2 ,..., Аm , |
В C . |
|
|
Пример 3.13. Докажите, что А (В С), D 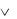 A, B D C . Решение.
A, B D C . Решение.
(1) |
А |
(В |
С) (р) |
|
(2) |
|
|
|
(р) |
|
D |
A |
||
(3) |
B |
|
(р) |
|
(4) |
D |
|
(р) |
|
(5) |
A |
|
(2,4t) |
|
(6) |
B |
С |
(1, 5t) |
|
(7) |
С |
|
(3, 6t) |
|
(8) |
D |
C |
(4, 7ср) |
|
С изложенным выше связан, но отличается от него вопрос о непротиворечивости множества высказываний, которое предлагается рассматривать как систему посылок для вывода. Множество
75

высказываний непротиворечиво, если существует по меньшей мере одно такое распределение истинностных значений простым компонентам, что все А одновременно получают значение 1. Противоречивость множества высказываний есть отрицание его непротиворечивости. Так, {А1 , А2 ,..., Аm } есть противоречивое множество, если при всяком распределении истинностных значений простым компонентам по меньшей мере одно из А получает значение 0.
Противоречие есть формула, которая всегда принимает
истинностное значение 0. |
Например А |
|
|
|
||||
А . |
|
|||||||
|
Теорема |
2. Множество |
высказываний {А1 , А2 ,..., Аm } противоречиво, |
|||||
если из него в качестве |
логического следствия можно вывести |
|||||||
противоречие. |
|
|
|
|
|
|
|
|
|
Пример |
3.14. |
Исследуйте |
противоречивость |
множества |
|||
|
|
|
|
|
|
|
|
|
высказываний:
АВ, В С, С D, А D, D .
Решение. Примем их как систему посылок и исследуем, какие выводы можно из них сделать.
(1) |
|
А |
В |
(р) |
||||
(2) |
|
В |
С |
(р) |
||||
(3) |
|
|
|
|
|
|
|
(р) |
С |
D |
|||||||
(4) |
|
|
|
|
|
|
|
(р) |
|
А |
D |
||||||
(5) |
|
|
|
|
|
|
|
(р) |
|
D |
|
|
|||||
(6) |
|
|
|
|
|
|
(5,4t) |
|
|
|
|
|
|
|
|
||
|
А |
|
|
|||||
(7) |
|
А |
|
|
(6t) |
|||
(8) |
|
А |
С |
(1,2t) |
||||
(9) |
С |
|
|
(7,8t) |
||||
|
|
|
|
(3,5t) |
||||
(10) С |
|
|
||||||
(11) С |
|
|
(9,10t) |
|||||
С |
||||||||
Мы заключаем, что множество противоречиво.
Задача 3.18. Исследуйте противоречивость систем посылок:
а) А (В С), D Е G, G (H I ), C E H .
б) А B С D, D E G, A G .
76

Противоречия играют важную роль в методе косвенного доказательства (доказательства от противного). Основой такого
доказательства служит: |
|
|
|
|
|
|
|
|||||||||||||
Теорема. А1 , А2 ,..., Аm |
B , если в качестве логического следствия из |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
А1 , А2 ,..., Аm |
и |
B |
|
можно вывести противоречие. |
||||||||||||||||
Пример 3.15. Докажите, что (С G) (D S ), S G E, |
|
|
|
|
|
. |
||||||||||||||
|
C |
D |
||||||||||||||||||
E |
||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
||||||||||||
(1) |
(С |
|
|
|
|
G) |
(D S) |
(р) |
||||||||||||
(2) |
S |
|
|
G |
E |
(р) |
||||||||||||||
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
(р) |
|||||||
|
E |
|
|
|
|
|
|
|
|
|||||||||||
(4) |
|
|
|
|
|
|
|
|
|
(р) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
C |
|
D |
|
|||||||||||||||||
(5) |
С |
D |
|
(4t) |
||||||||||||||||
(6) |
С |
|
|
|
|
|
|
|
|
(5t) |
||||||||||
(7) |
(С |
|
|
|
|
G) |
|
(1t) |
||||||||||||
(8) |
G |
|
|
|
|
|
|
|
|
(6,7t) |
||||||||||
(9) |
(D |
|
|
|
|
S) |
|
(1t) |
||||||||||||
(10) |
D |
|
|
|
|
|
|
|
|
(5t) |
||||||||||
(11) |
S |
|
|
|
|
|
|
|
|
(9,10t) |
||||||||||
(12) |
S |
|
|
G |
|
(8,11t) |
||||||||||||||
(13) |
E |
|
|
|
|
|
|
|
|
(2,12t) |
||||||||||
(14) |
|
|
|
|
|
|
|
(3,13t) |
||||||||||||
Е |
|
|
E |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким |
образом, |
доказано, что C |
D |
есть логическое следствие |
|||||||||||||
имеющихся посылок. |
|
|
|
|
|
|
|
|
|||||||||
Задача 3.19. Докажите, что: |
|||||||||||||||||
1) |
|
|
|
|
|
|
|
S . |
|
|
|
|
|
|
|
|
|
H |
S, |
H |
|
|
|
|
|
|
|
|
|||||||
2) |
J |
W , |
|
J |
C, |
W |
|
C . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3) |
|
А |
В, |
С |
В |
А |
С . |
||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А В, А С, В D C D . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A (B F) . |
||
А (В С), (С D) |
|
E, F (D E ) |
|
|
|||||||||||||||
6) W P J , J C S, |
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
S U , |
|
C U |
W |
|||||||||||||||
7) (С G) (D S ), S G E, |
|
|
|
|
|
||||||||||||||
E C D . |
|||||||||||||||||||
8) А В, С D, А С В D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
77
Глава 4. ЛОГИКА ПРЕДИКАТОВ
4.1 Основные понятия
Логика предикатов представляет собой развитие логики высказываний. С помощью формул логики высказываний можно описать и исследовать структуру сложных высказываний, установить их истинность или ложность в зависимости от истинности или ложности входящих в неё простых высказываний. Для описания внутренней логической структуры простых высказываний используется понятие предиката (лат. praedicatum – логическое сказуемое).
Пусть имеется ряд простых высказываний: Р1 : «Иван читает Достоевского», Р2 : «Пётр читает Достоевского»,
. . .
Рn : «Степан читает Достоевского».
Вместо высказываний Р1, Р2, ..., Рn мы могли бы ввести одноместный предикат Р(х), для которого переменная х принимала бы значения из предметной области М = {Иван, Пётр, ..., Степан}, а сама предикатная функция переводилась бы словами Р(х): «х читает Достоевского».
Вводя в предикате переменную, заменяющую нужный предмет, мы получаем высказывательную функцию в том смысле, что для каждого значения переменной х (из соответствующей области определения) результат есть высказывание.
Сразу же напишем обобщение, а именно распространение сказанного на высказывательные функции со многими переменными. Вот несколько примеров:
R(x, y) : " x2 y2 0";
Q(x, y, z) : "x2 y2 z2".
n-местный предикат – это функция Р(х1, х2, ..., хn) от n переменных, принимающих значения из некоторых заданных предметных областей, так
78

что x1 M1 , x2 M 2 , ..., xn M n , а функция Р принимает два логических значения – «истинно» или «ложно»:
Р(х1, х2, ..., хn) : М1 М2 |
... Мn → {0, 1}. |
Иными словами, предикат – это переменное высказывание. |
|
Аргументами высказывательной |
функции являются предметные |
переменные, которые обозначают строчными буквами латинского алфавита х, у, z. Эта функция приобретет значение 1 или 0 только при подстановке в высказывательную функцию вместо предметных переменных их конкретных значений. Конкретные значения аргументов высказывательной функции называют предметными постоянными, которые обозначают строчными буквами латинского алфавита а, в, с, .
Если высказывательная функция содержит один аргумент, то задан одноместный предикат, если она содержит n аргументов, то – n-местный предикат. Одноместный предикат, как правило, описывает наличие какого-либо признака у предмета, а n-местный предикат наличие отношений между n предметами. Следует еще раз обратить внимание, что когда все предметные переменные замещены предметными постоянными, тогда предикат превращается в высказывание.
Для удобства в число значений n включаем и 0, понимая под 0- местным предикатом высказывание, т.е. предикат, в котором нет переменных для замены.
Пример 4.1. В следующих высказываниях выделите входящие в них предикаты и запишите эти высказывания с помощью символики исчисления предикатов.
1. Снег белый.
Решение. Φ(снег), где Φ(х) обозначает предикат: «х – белый». 2. Два меньше трёх.
Решение. Φ(2, 3), где Φ(х, у): «х < y».
Предикат Р(х1, х2, ..., хn), заданный на множествах М1, М2, ..., Мn, называется:
а) тождественно истинным, если при любой подстановке вместо переменных х1, х2, ..., хn любых конкретных предметов а1, а2, ... , аn из
79
множеств М1, М2, ..., Мn соответственно он превращается в истинное высказывание Р(а1, а2, ... , аn);
б) тождественно ложным, если при любой подстановке конкретных предметов из множеств М1, М2, ... , Мn соответственно он превращается в ложное высказывание;
в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов а1, а2, ... , аn из множеств М1, М2, ... , Мn соответственно при подстановке которых вместо соответствующих предметных переменных в предикат Р(х1, х2, ... , хn) последний превратится в истинное (ложное) высказывание Р(а1, а2, ... , аn).
Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов:
1)каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2)каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3)каждый нетождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4)каждый нетождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.
Два n-местных предиката Р(х1, х2, ... , хn) и Q(х1, х2, ... , хn), заданных над одними и теми же множествами М1, М2, ... , Мn, называются
равносильными |
(эквивалентными), |
если набор предметов |
a1 M1 , |
a2 M 2 , ..., |
an M n превращает |
первый предикат в |
истинное |
высказывание Р(а1, а2, ... , аn) в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание
Q(а1, а2, ... , аn).
Утверждение о равносильности (эквивалентности) двух предикатов Р и Q символически будем записывать так: Р 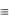 Q.
Q.
Задача 4.1. Заданы предикаты:
P(x, y, z) : "x2 y2 z2";
Q(x, y) : " y (x 4) /( x 4)";
80
