5543

участнику игры требуется узнать цвет и марку машины, но при этом каждый участник игры, видевший фотографию, либо цвет, либо марку машины называет неправильно.

Участник Х сказал: синяя «волга». Участник У сказал: черный «москвич». Участник Z сказал: «жигули», но не синяя. Как узнать цвет и марку машины? Решение.

Имеется шесть элементарных высказываний: синяя машина} А – «синяя машина»; В – «волга»;

С – «чёрная машина»; D – «москвич»;

Е– «жигули»;

А– «не синяя машина».

Так как либо цвет, либо марку машины каждый участник игры назвал правильно, то для высказываний каждого участника будет истинна дизъюнкция их элементарных высказываний:

Х: А В 1; У: С D 1; Z: E A 1.

Поскольку эти три высказывания, представляющие собой дизъюнкцию элементарных высказываний, истинны, то истинна и их конъюнкция: ( А В) (C D) (E A) 1.

Раскроем все скобки:

А C E A D E B C E B D E A C A A D A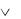

B C A B D A 1.

Данная дизъюнкция имеет вид:

0 0 0 0 0 0 (B С A 1) 0 1.

Ответ: на фотографии была чёрная «волга».

Задача 3.10. Истинно или ложно высказывание (А В) (В С), если высказывания В и С истинны?

Задача 3.11. Докажите, что (А В) С (А С) (В С). Задача 3.12. Для высказываний А, В и С докажите формулы:

61

5) А (В С) ( А В) ( А С);

6) А (В С) ( А В) ( А С).

Задача 3.1. Упростите выражения:

4) ( А В С 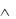A) (D В D ) (B С) .

3.5 Основные логические законы

Закон мышления – это необходимая, существенная, устойчивая связь между мыслями. Среди множества логических законов логика выделяет четыре основных, выражающих коренные свойства логического мышления

– его определённость, непротиворечивость, последовательность и обоснованность. Это законы тождества, противоречия, исключённого третьего и достаточного основания. Они действуют в любом рассуждении, при правильном их применении люди однозначно понимают друг друга, однозначно толкуют информацию и делают выводы, адекватные этой информации.

Закон тождества. Любая мысль в процессе рассуждения должна иметь определённое, устойчивое содержание. Это коренное свойство мышления – его определённость – выражает закон тождества: всякая мысль в процессе рассуждения должна быть тождественна самой себе

( А А ).

Из закона тождества следует: нельзя отождествлять различные мысли, нельзя тождественные мысли принимать за нетождественные.

62

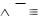
Нарушение этого требования в процессе рассуждения нередко бывает связано с различным выражением одной и той же мысли в языке.

Широко применяется закон тождества в точных науках. С помощью закона тождества даются формулировки теорем, определения понятий, различные формулы и т.д.

Мы используем закон тождества при решении любой задачи по заданному алгоритму, отождествляя условие конкретной задачи с известными приёмами её решения.

Если закон тождества выражает логическую однозначность и определённость мышления, то закон противоречия выражает его последовательность и непротиворечивость.

Закон противоречия. Два противоречивых суждения не могут быть истинными в одно и то же время и в одном и том же отношении

( А А 0).

Для правильного его понимания необходимо иметь в виду следующее. Утверждая что-либо о каком-либо предмете, нельзя, не противореча себе, отрицать то же самое о том же самом предмете, взятом в то же самое время и в том же самом отношении.

Так, не могут быть одновременно истинными следующие четыре типа простых суждений:

1.«Данное S есть Р» и «Данное S не есть Р».

2.«Ни одно S не есть Р» и «Все S есть Р».

3.«Все S есть Р» и «Некоторые S не есть Р».

4.«Ни одно S не есть Р» и «Некоторые S есть Р».

Сознательное использование закона противоречия помогает обнаруживать и устранять противоречия в своих и чужих рассуждениях, вырабатывает критическое отношение ко всякого рода неточности, непоследовательности в мыслях и действиях.

Особое значение имеет закон противоречия в ходе проведения доказательств. Он лежит в основе требований, накладываемых на доказательства. Непротиворечивыми должны быть как используемые в доказательстве посылки (тезисы и аргументы), так и выводы этой теории.

63

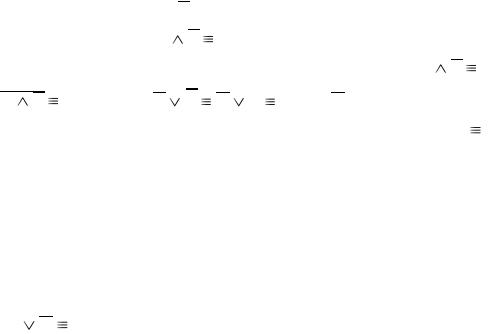
В математике закон противоречия используется и при доказательстве методом от противного. Пусть дано истинное суждение А и надо доказать справедливость В. Метод от противного заключается в том, что вместо В берут его отрицание В и затем с помощью математических аргументов доказывается, что А В 0 . Если удаётся это доказать, то в результате делается вывод, что В – истинно. Проверим это: А В 0 равносильно

АВ 1, значит, А В А В 1 , но А – ложно, т.е. для того чтобы

значение дизъюнкции было равно 1, необходимо, чтобы В 1.

Закон противоречия устанавливает, что утверждение и отрицание одной и той же мысли не могут быть одновременно истинными. На вопрос, могут ли они быть одновременно ложными, даёт ответ закон исключенного третьего.

Закон исключённого третьего. Два противоречащих суждения не могут быть одновременно ложными, одно из них необходимо истинно

( А А 1).

Противоречащими называются суждения, в одном из которых что-либо утверждается (или отрицается) о каждом предмете некоторого множества, а в другом – отрицается (утверждается) о некоторой части этого множества. Эти суждения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно, то другое ложно, и наоборот. Противоречащими являются также два суждения об одном предмете, в одном из которых чтолибо утверждается, а в другом то же самое отрицается. Одно из этих суждений необходимо истинно, другое – необходимо ложно.

Подобно закону противоречия закон исключённого третьего выражает последовательность, непротиворечивость мышления, не допускает противоречий в мыслях. Вместе с тем, действуя только в отношении противоречащих суждений, он устанавливает, что два противоречащих суждения не могут быть не только одновременно истинными (на что указывает закон непротиворечия), но также и одновременно ложными: если ложно одно из них, то другое необходимо истинно, третьего не дано.

Закон исключённого третьего работает в процессе построения умозаключений и доказательств. С помощью закона исключённого

64

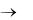
третьего проводятся косвенные доказательства, так как для того, чтобы установить истинность доказываемого тезиса, надо выявить ложность противоречащего суждения.

Закон исключённого третьего применяется там, где познание имеет дело с жёсткой ситуацией: или – или, истинно – ложь. На законе исключённого третьего основана вся математическая логика.

Закон достаточного основания. Всякая мысль признаётся истинной, если она имеет достаточное основание.

Благодаря науке, которая в своих законах и принципах закрепляет общественно-историческую практику человечества, мы для обоснования наших мыслей не прибегаем всякий раз к их проверке, а обосновываем их логически, путём выведения из уже установленных положений.

Таким образом, достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и установленная мысль, из которой с необходимостью вытекает истинность данной мысли.

Обоснованность – важнейшее свойство логического мышления. Во всех случаях, когда мы утверждаем что-либо, убеждаем в чём-либо других, мы должны доказывать наши суждения, приводить достаточные основания, подтверждающие истинность наших мыслей. В этом состоит коренное отличие научного мышления от мышления ненаучного, которое характеризуется бездоказательностью, способностью принимать на веру различные положения и догмы.

Закон достаточного основания имеет важное теоретическое и практическое значение. Фиксируя внимание на суждениях, обосновывающих истинность выдвинутых положений, этот закон помогает отделить истинное от ложного и прийти к верному выводу.

3.6. Необходимое и достаточное условие импликации

Если высказывание А В является истинным, то его называют

теоремой.

Например, следующее утверждение является теоремой: «Если натуральное число n делится на 6, то число n делится на 3».

65

Условием (или посылкой) этой теоремы является предложение «Натуральное число n делится на 6», а заключением – предложение «(Натуральное) число n делится на 3».

Вформе «если ..., то ...» можно записывать разные утверждения. Например, рассмотрим следующее утверждение: «Если число n делится на 6, то число n нечётное». В этом примере из предположения истинности условия утверждения уже не следует истинность заключения. Поэтому сформулированное утверждение не является теоремой.

Вкаждой теореме можно выделить заключение и условие этой теоремы. Условие теоремы называется достаточным условием для заключения теоремы.

Так, в теореме «Если натуральное число n делится на 6, то число n делится на 3» условие «Число n делится на 6» достаточно для того, чтобы число n делилось на 3.

Заключение теоремы называют необходимым условием для условия этой теоремы.

Так, в теореме «Если натуральное число n делится на 6, то число n делится на 3» заключение «Число n делится на 3» необходимо, чтобы «Число n делилось на 6». Другими словами, если натуральное число n не делится на 3, то число n не может делиться на 6.

Для каждой теоремы можно записать обратное утверждение,

противоположное утверждение и противоположное обратному.

Импликацию В А, полученную из А В перестановкой условия и заключения, называют конверсией (обратным высказыванием) для А В .

Снова рассмотрим теорему: «Если натуральное число n делится на 6, то число n делится на 3». Утверждение, обратное к этой теореме, имеет следующий вид: «Если натуральное число n делится на 3, то число n делится на 6». Полученное в этом примере обратное утверждение не является теоремой, потому что из делимости натурального числа n на 3 не следует делимость числа n на 6. В этом очень легко убедиться на примере: число 9 делится на 3, но не делится на 6.

Рассмотрим теперь теорему «Если натуральное число n делится на 2 и делится на 3, то число n делится на 6». Утверждение, обратное к этой

66

теореме, имеет следующий вид: «Если натуральное число n делится на 6, то число делится на 2 и делится на 3».

В этом примере полученное обратное утверждение является теоремой. Таким образом, утверждение, обратное к некоторой теореме, иногда

тоже является теоремой, а иногда не является теоремой.

Импликацию А В , полученную из А В заменив и условие, и заключение их отрицаниями, называют инверсией (противоположным

Полученная таблица позволяет сделать следующие выводы. Условное высказывание и его контрапозиция являются

равносильными (логически эквивалентными).

Высказывание обратное и противоположное условному являются равносильными (логически эквивалентными).

Импликация не обладает переместительным свойством, т.е. если

Итак, прямая и обратная импликации не равны между собой, но прямая и обратная теоремы не всегда имеют противоположный смысл.

67

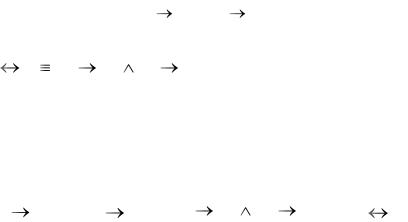
Существуют такие высказывания, для которых одновременно справедливы и прямая, и обратная импликации, т.е. А В и В А. Такие логические операции называются эквиваленцией. На языке логических операций это

Вслучае, если условие теоремы содержит слова «необходимо и достаточно», при её доказательстве нужно доказать не только прямую теорему, но и обратную.

Слова необходимо и достаточно можно заменить словами «тогда и только тогда, когда», логическую операцию импликации – эквиваленцией.

Например, рассмотрим известную теорему, которая имеет следующую формулировку: «Натуральное число n делится на 3 тогда и только тогда, когда сумма цифр числа n делится на 3».

Такая формулировка объединяет в себе две взаимно обратное теоремы. Теорема 1. Если натуральное обратное число n делится на 3, то

сумма цифр числа n делится на 3.

Теорема 2. Если сумма цифр натурального числа n делится на 3, то число n делится на 3.

Вэтом примере условие делимости на 3 суммы цифр натурального числа n является необходимым и достаточным для делимости числа n на 3.

Всвою очередь условие делимости на 3 натурального числа n является необходимым и достаточным для делимости на 3 суммы цифр числа n.

Пример 3.8. Какие из следующих шести приведённых ниже

импликаций являются по отношению друг к другу обратными,

68

противоположными, противоположными обратным? Какие из них являются теоремами?

1) если каждое из натуральных чисел делится на 7, то и их сумма делится на 7;

2)если ни одно из двух чисел не делится на 7, то их сумма не делится на 7;

3)если хотя бы одно из двух чисел делится на 7, то и сумма делится на 7;

4)если сумма двух чисел делится на 7, то каждое слагаемое делится на 7;

5)если сумма двух чисел не делится на 7, то ни одно из слагаемых не делится на 7;

6)если сумма двух чисел не делится на 7, то хотя бы одно из слагаемых не делится на 7.

Решение. Пусть А – утверждение, что каждое из двух слагаемых делится на 7; В – сумма делится на 7; С – по крайней одно из слагаемых делится на 7.

Тогда приведённые выше импликации можно записать:

1) А В;

2)С В ;

3)С В;

4) В А ;

5)В С ;

6)В А .

Таким образом, 1 и 4, 2 и 5 импликации являются взаимнообратными; 2 и 3, 4 и 6 – взаимно противоположными; 1 и 6, 3 и 5 являются противоположными; 1 и 6 импликации являются теоремами.

Задача 3.14. В каждой из приведённых ниже импликаций выделите условие и заключение. Сформулируйте импликацию, противоположную данной и обратную противоположной. Определите, истинны они или ложны.

1)если вы находитесь в Африке, то вы находитесь южнее Москвы.

2)если я учусь в школе, то мне больше, чем два года.

3)если последняя цифра числа 17 равна 5, то оно делится на 5.

4)если сумма цифр числа 25 делится на 3, то это число делится на 3.

5)если сумма цифр числа 23 делится на 5, то это число делится на 5. Задача 3.15. Для каждой из приведённых ниже импликаций

69

сформулируйте обратную, противоположную и противоположную обратной. Какие из них являются теоремами?

1.Если число делится на 9, то сумма его цифр делится на 3.

2.Если натуральное число делится на 3 и на 5, то оно делится на 15.

3.Произведение двух положительных чисел положительно.

3.7 Нормальные формы формул логики высказываний

В алгебре высказываний используют две нормальные формы:

дизъюнктивную (ДНФ) и конъюнктивную нормальные формы формулы

(КНФ).

Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.

ДНФ есть формула, имеющая вид дизъюнкции элементарных конъюнкций, т.е.

элементарных конъюнкций содержит пропозициональную переменную и её отрицание F F , то следует удалить всю элементарную конъюнкцию, т.к. F F 0 .

Процедура приведения к ДНФ:

1. Все отрицания «спустить» до переменных применяя правило:

2. Раскрыть скобки применяя закон:

70