
5543
.pdf
Например, пусть А – множество юношей и девушек обучающихся на 1-м курсе в институте, а В – множество всех девушек, которые обучаются в данном институте. Тогда А\В – множество всех юношей, которые обучаются на 1-м курсе.
Пусть имеется некоторое универсальное множество U такое, что все рассматриваемые множества есть его подмножества. Например, возьмём множество книг. В это множество входят подмножества научных, художественных книг, книг по искусству; среди научных книг есть подмножества книг по математике, химии, биологии и т.д. Множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг. Сколько этих подмножеств? Чтобы ответить на этот вопрос, рассмотрим другой пример. Пусть универсальное множество состоит из трёх элементов: а, в, с . Перечислим все подмножества U: а , в , с , а, в , а, с , в, с , а, в, с , Ø. Их всего 23 = 8 подмножеств. Если универсальное множество U состоит из п элементов, то число всех подмножеств множества U равно 2п .
Пусть множество А есть некоторое подмножество универсального множества U. Дополнением множества А называется множество А (рисунок 1.4) элементами которого являются все элементы, не входящие в А, но принадлежащие U.
|
|
А . |
||
А а |
а |
|||
|
|
|
|
|
|
|
|
|
|
|
U |
А |
||
|
А |
|
|
|
|
|
|
|
|
Рисунок 1.4 – Множество А
Например, если U = {целые числа}, А= {чётные числа}, то А = {нечётные числа}.
Для любых подмножеств А, В, С и универсального множества U выполняются следующие тождества:
1) коммутативность пересечения и объединения:
11

АВ В А,
АВ В А;
2)ассоциативность пересечения и объединения:
А (В С) |
( А В) С, |
А (В С) |
(А В) С; |
3) дистрибутивность пересечения и объединения относительно друг друга:
( А В) С ( А С) (В С), ( А В) С ( А С) (В С);
4)А А U , А А 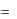 Ø;
Ø;
5)А Ø= А, А U = А;
6)А А= А, А А= А;
7)А U = U, А Ø = Ø;
8)закон двойственности – закон де Моргана:
АВ А В ,
АВ А В;
9)закон поглощения:
А ( А В) |
А, |
А ( А В) |
А. |
Данные тождества позволяют упрощать различные сложные выражения, содержащие множества, подобно тому как такие упрощающие
тождественные преобразования делаются в алгебре. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.1. Упростите выражение А В |
B |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. А В |
B |
A B |
B A |
B. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 1.2. Упростите выражение |
|
|
|
|
|
|
|
|
|
|
|
|
B C) |
|
|
|
|
|
|
|||||||||||
|
|
( A |
|
|
B |
C) |
( A |
|
B |
C. |
||||||||||||||||||||
|
|
|
|
|
|
B C) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. ( A B |
C) |
|
( A |
|
B |
C |
A |
A |
B C |
B |
C |
|||||||||||||||||||
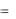 U B C
U B C B C
B C 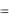 B C
B C 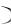 B C U .
B C U .
Задача 1.1. Какие из следующих утверждений верны для всех множеств А, В и С?
1. Если А |
В |
и |
В |
С, то А |
С. |
2. Если А |
В |
и |
В |
С, то А |
С. |
3. Если А |
В |
и |
В |
С, то А |
С. |
4. Если А |
В |
и |
В |
С, то не верно, что С А. |
|
12
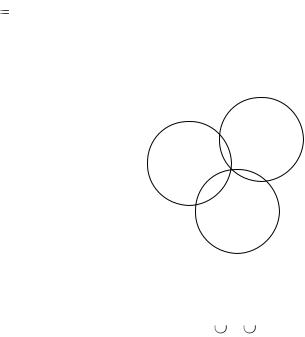
Пример 1.3. Из 20 человек двое изучали только английский язык, трое – только немецкий, шестеро – только французский. Никто не изучал трёх языков. Один изучал немецкий и английский, трое – французский и английский. Сколько человек изучали французский и немецкий языки?
Решение. Обозначим через А множество учеников, изучавших английский язык, через В – немецкий язык, через С – французский язык.
По условию |
А В содержит один элемент, |
А С содержит 3 элемента, |
||
А В С Ø |
(никто не изучал сразу три языка). Требуется определить |
|||
количество элементов в пересечении В С . |
Изобразим эти множества на |
|||
диаграмме Венна (рисунок 1.5). |
|
|
|
|
|
|
|
3 |
|
|
2 |
1 |
В |
|
|
|
|
||
|
А |
3 |
|
|
|
|
|
6 |
|
|
|
|
С |
|
Рисунок 1.5 – Диаграмма Венна
Объединение множеств А В С содержит 20 элементов. Из диаграммы видно, что множество В С должно содержать 20 – 1 – 2 – 3 – 6 – 3 = 5 элементов. Значит, французский и немецкий языки изучали 5 человек.
Задача 1.2. Из 220 студентов 163 играют в баскетбол, 175 – в футбол, 24 не играют в эти игры. Сколько человек одновременно играют в баскетбол и футбол?
Задача 1.3. В группе 30 студентов. Все, кроме двух, имеют оценки «5», «4» и «3». Число студентов, имеющих оценки «5» – двадцать, «4» – четырнадцать, «3» – шестнадцать. Трое учатся на «5» и на «3», трое – лишь на «5» и на «4» и четверо – лишь на «4» и на «3». Сколько человек имеют одновременно оценки «5», «4», «3».
Задача 1.4. Анкетирование, проведённое среди 57 студентов, показало, что в шахматы умеют играть 35 человек, в шашки – 40 человек, причём в обе игры умеют играть 21 человек. Сколько человек не умеют играть ни в шахматы, ни в шашки?
13

Задача 1.5. Приняв множество первых 20 натуральных чисел в качестве универсального множества, записать следующие его подмножества: А – множество чётных чисел, В – множество нечётных чисел, С – множество квадратов чисел, D – множество простых чисел?
Если Р(х) есть свойство, а f – функция, то через f (x) P(x)
мы будем обозначать множество всех таких у, для которых имеется х, обладающий свойством Р(х) и такой, что у=f(х). Например, вместо того, чтобы писать {у| имеется такой х, что х есть целое число и у=2х}, мы будем писать
2x x Z .
|
Пример 1.4. Даны |
два |
|
множества: |
А |
6к 5 |
|
к |
0,1,2,... |
и |
||||||
|
|
|||||||||||||||
В |
3m 2 |
|
m |
0,1,2,... . Найдите: а) |
А |
B ; б) А B ; с) B \ А. |
|
|
|
|
||||||
|
|
|
|
|
||||||||||||
|
Решение. Множеству А принадлежат числа 5, 11, 17, 23, 29, … и |
не |
||||||||||||||
принадлежат числа 0, 1, 2, 3, 4, 6, 7, 8, 9, … |
|
|
|
|
|
|
|
|||||||||
|
Множеству В принадлежат числа 2, 5, 8, 11, 14, 17, … и не |
|||||||||||||||
принадлежат числа 0, 1, 3, 4, 6, 7, 9, 10, … |
|
|
|
|
|
|
|
|||||||||
|
Найдём объединение множеств: |
А B =В. |
|
|
|
|
|
|
|
|||||||
|
Найдём пересечение множеств: А B =А. |
|
|
|
|
|
|
|
||||||||
|
Найдём разность множеств: |
|
B \ А= 2,8,14,20,... . Это множество можно |
|||||||||||||
задать также в виде: B \ А |
6к 2 |
|
к |
0,1,2,... . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1.6. Даны |
два |
|
множества: |
|
|
|
|
и |
|||||
|
Задача |
|
А |
2к |
|
к |
0,1,2,... |
|||||||||
В |
2m |
1 |
|
m 0,1,2,... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите: а) А B ; б) А B ; с) B \ А.
Задача 1.7. Изобразите на числовой оси и запишите с указанием характеристического свойства следующие множества: А B , А B , А \ В , B \ А, где
А |
х |
|
х |
п , |
В |
х |
|
п |
5 |
x |
n |
10 |
– чётный вариант, |
||||
А |
х |
|
х |
п , |
В |
х |
|
п |
5 |
x |
n |
10 |
– нечётный вариант, |
||||
|
|
||||||||||||||||
п – помер варианта. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 1.8. Упростите выражение |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
( A B C X ) |
( A C) |
(B C) (C X ). |
||||||||||
14

1.2 Бинарные отношения. Свойства бинарных отношений
Отношения – один из способов задания взаимосвязей между элементами множества.
Унарные (одноместные) отношения отражают наличие какого-то определённого признака R (свойства и т.п.) у элементов множества М. Тогда все такие элементы a из множества М, которые отличаются данным признаком R, образуют некоторое подмножество в М, называемое унарным отношением R, т.е. a R и R M.
Двухместным (бинарным) отношением R называется подмножество пар (a, b) R прямого произведения М1  М2, т.е. R M1 M 2. Бинарные (двухместные) отношения используются для определения каких-либо взаимосвязей, которыми характеризуются пары элементов прямого
М2, т.е. R M1 M 2. Бинарные (двухместные) отношения используются для определения каких-либо взаимосвязей, которыми характеризуются пары элементов прямого
произведения М1 |
М2. |
При этом |
множество М1 называется областью определения |
отношения R, множество М2 – областью значений. Часто рассматривают отношения R между парами элементов одного и того же множества М,
тогда R M |
M. |
Если |
a, b находятся в |
отношении R, это |
часто |
||
записывается как aRb. |
|
|
|
|
|
||
Пусть R |
A |
B определено |
в соответствии с |
изображением на |
|||
рисунке 1.6. Область определения D(R) и область значений Q(R) |
|||||||
определяются соответственно: D(R) |
{a | (a, b) |
R}, Q(R) |
{b | (a, b) |
R} . |
|||
|
|
|
|
R |
|
|
|
А |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
Элементы А, не |
Элементы А и B |
Элементы B, не |
|||||
включённые в R |
включённые в R |
включённые в R |
|||||
|
|
|
Рисунок 1.6 – R |
A B |
|
|
|
15

Способы задания бинарных отношений – любые способы задания множеств (так как отношения определены как подмножества некоторых множеств – прямых произведений). Отношения, определённые на конечных множествах, обычно задаются:
1. Списком (перечислением) пар, для которых это отношение выполняется. Например, R 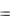 (a, b), (a, c), (b, d ) .
(a, b), (a, c), (b, d ) .
2. Матрицей – бинарному отношению R M M , где М = {a1, a2, …, an}, соответствует квадратная матрица порядка n, в которой элемент сij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если между ai и aj имеет место отношение R, или 0, если оно отсутствует:
Сij |
1, |
если ai Ra j , |
|
0 в противном случае. |
|
||
|
|
||
Пример 1.5. Пусть М = {1, 2, 3, 4, |
5, 6}. Задайте в явном виде |
||
(списком) и |
матрицей отношение R M |
M , если R означает «быть |
|
строго меньше».
Решение. Отношение R как множество содержит все пары элементов a, b из М такие, что a < b:
R 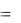 (a, b) a, b M , a b .
(a, b) a, b M , a b .
Тогда
R = { (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}.
Матрица отношения:
|
R |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
2 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
3 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
4 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
5 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Задача 1.9. Пусть М = {1, 2, 3, 4, 5, 6}. Составьте матрицы |
||||||||
отношения R1, R2 , R3 M |
M , если |
|
|
|
|
|||
16

а) R1 – «Быть делителем»;
б) R2 – «Иметь общий делитель, отличный от единицы»;
в) R3 – «Иметь один и тот же остаток от деления на 3».
Пример 1.6. Для отношения R, заданного в примере 1.3, установите область определения и область значений.
Решение. Область определения D(R) = {1, 2, 3, 4, 5}, область
значений Q(R) = {2, 3, 4, 5, 6}. |
|
|
Пусть R – отношение на множестве M, R |
M |
M . |
Свойства бинарных отношений: |
|
|
1) R – рефлексивно, если имеет место |
aRа |
для любого a M |
(например, отношение «Жить в одном городе» – рефлексивно); |
||
2) R – антирефлексивно, если ни для какого a |
M не выполняется |
|
aRа (например, отношение «Быть сыном» – антирефлексивно);
3)R – симметрично, если aRb влечёт bRa (например, отношение «Работать на одной фирме» – симметрично);
4)R – антисимметрично, если aRb и bRa влекут a = b, т.е. ни для каких различающихся элементов a и b (a ≠ b) не выполняется одновременно aRb и bRa (например, отношения «Быть сыном», «Быть начальником» – антисимметричны);
5)R – транзитивно, если aRb и bRс влекут aRс (например, отношения «Быть моложе», «Быть братом» – транзитивны).
Пример 1.7. Каковы свойства отношений, заданных:
1)на множестве натуральных чисел N для R1 – «Быть не больше ≤»;
2)на множестве людей для R2 – «Быть сыном»;
3)на множестве элементов структуры (рисунок 1.7) для R3 – «Быть непосредственно связанным с».
Решение
1)На множестве N, R1 = {(a, b) | a ≤ b}:
–рефлексивно, неантирефлексивно, так как выполняется a ≤ a для всех a M , например, 2 ≤ 2;
–несимметрично, так как 2 ≤ 3, но неверно, что 3 ≤ 2;
–антисимметрично, поскольку если a ≤ b, а b ≤ a, то a = b;
17

–транзитивно, так как если a ≤ b, а b ≤ с, то а ≤ с, например, 2 ≤ 3, 3 ≤ 4 и 2 ≤ 4;
2) R2 = {(a, b) | a – сын b} на множестве людей:
–нерефлексивно, антирефлексивно, так как ни для каких а не выполняется: а – сын а;
–несимметрично, антисимметрично, поскольку ни для каких a ≠ b не выполняется: а – сын b и b – сын a;
–нетранзитивно, так как если: а – сын b и b – сын с, то а – не сын с; 3) R3 = {(a, b) | a – непосредственно связан с b} на множестве
элементов структуры
a
b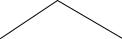 c
c
d e |
f |
g |
h |
|
Рисунок 1.7 – Множество элементов структуры
–нерефлексивно, антирефлексивно, если в конкретной интерпретации aR3а не имеет смысла;
–симметрично, неантисимметрично, поскольку для всех a ≠ b, если выполняется aR3b, то bR3a;
–нетранзитивно, так как при aR3b и bR3с не выполняется aR3с (a и с связаны, но опосредованно).
Задача 1.12. Какими свойствами характеризуются следующие отношения на М = {1, 2, 3, ..., 9}:
а) R1 = {(a, b) | (a – b) – чётное}; б) R2 = {(a, b) | (a + b) – чётное};
в) R3 = {(a, b) | (a + 1) – делитель (a + b)}.
18
1.3 Эквивалентность и порядок. Операции над бинарными отношениями
Отношением эквивалентности (или просто эквивалентностью)
называют бинарное отношение на множестве, если оно рефлексивно, симметрично, транзитивно. Например, отношение «Жить в одном городе» на множестве людей – эквивалентность.
Отношение эквивалентности имеет важную особенность: эквивалентность R разбивает множество М, на котором оно задано, на непересекающиеся подмножества так, что элементы одного и того же подмножества находятся в отношении R, а между элементами из разных подмножеств отношение R отсутствует. В таком случае говорят, что отношение R задаёт разбиение на множестве М, или систему классов эквивалентности по отношению к R. Мощность этой системы называется индексом разбиения. В то же время любое разбиение множества М на классы определяет некоторое отношение эквивалентности, а именно отношение «Входить в один и тот же класс данного разбиения».
Отношением нестрогого порядка (или нестрогим порядком)
называют бинарное отношение на множестве, если оно рефлексивно, антисимметрично, транзитивно, и отношением строгого порядка (строгим порядком), если оно антирефлексивно, антисимметрично, транзитивно. Оба эти отношения называют отношением порядка. Например, отношение «Быть не старше» на множестве людей, «Быть не больше» на множестве натуральных чисел – нестрогий порядок; отношения «Быть моложе», «Быть прямым потомком» на множестве людей – строгий порядок.
Элементы a, b M сравнимы по отношению порядка R на М, если выполняется aRb или bRa.
Множество М, на котором задано отношение порядка, может быть:
а) полностью упорядоченным множеством, если любые два элемента из М сравнимы по отношению порядка. В таком случае говорят, что отношение R задаёт полный порядок на множестве М. Например, отношение «Быть не старше» задаёт полный порядок на множестве людей;
19

б) частично упорядоченным множеством – в противном случае. При этом говорят, что отношение R задаёт на множестве М частичный порядок. Например, отношение «Быть начальником» задаёт на множестве сотрудников организации частичный порядок, так как, например, для пары сотрудников одного отдела данное отношение не выполняется: они несравнимы по данному отношению.
Пример 1.8. К каким типам отношений относятся:
1) отношение равносильности на множестве формул, описывающих элементарные функции (формулы равносильны, если они задают одну и ту же функцию, например, (a + b) ∙ (a – b) = а2 – b2);
2) отношение ≤ и < на множестве векторов длины n с компонентами из N, определяемые следующим образом:
а) (а1, ..., аn) ≤ (b1, …, bn), если a ≤ b1, …, an ≤ bn;
б) (а1, ..., аn) < (b1, …, bn), если (a1, …, an) ≤ (b1, …, bn ) и хотя бы в одной координате i выполняется аi < bi.
Решение. Отношения, заданные в п. 1, являются отношениями эквивалентности на соответствующих множествах; отношения, заданные в п. 2, являются отношениями порядка; при этом отношение ≤, определённое в п. 2, есть отношение нестрогого порядка, а отношение < в п. 2 – отношения строгого порядка.
Пример 1.9. Каков индекс разбиения и мощность классов эквивалентности по отношению Ri, если R:
1)отношение равенства (тождества) на любом множестве;
2)отношение «Иметь один и тот же остаток от деления на 5» на множестве натуральных чисел N?
Решение 1. Все классы эквивалентности по отношению равенства (тождества)
Е = {(a, b) | a = b} на любом множестве М, a, b M , состоят из одного элемента. Индекс разбиения М по отношению Е равен мощности тождества М, т.е. M .
2.Индекс разбиения множества N по заданному отношению R равен
5.Множества натуральных чисел, составляющие каждый класс эквивалентности, счётны.
20
