5543

– множеством рёбер, каждое из которых представлено парой своих концевых вершин: Е1 = {(v1, v4), (v4, v3), (v3, v5), (v5, v2)}.

Порядок указания вершин при описании ребра здесь безразличен, так как все рёбра в графе G неориентированные.

В общем виде задать граф – значит описать множества его вершин и рёбер, а также отношение инцидентности. Для описания вершин и рёбер достаточно их занумеровать. Пусть v1, v2, ..., vj, ...,vn – вершины графа G; e1, e2, ..., ei, ...,em – рёбра. Отношение инцидентности задаётся:

– матрицей инцидентности ||εij|| размера m 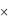n: по вертикали и горизонтали указываются вершины и рёбра соответственно, а на пересечении i-й вершины и j-го ребра:

в случае неориентированного графа проставляется 1, если они инцидентны, и 0 – в противном случае, т.е.

(следует отметить, что в каждой строке матрицы количество единиц равно двум, а в каждом столбце равно степени вершины ρ1(vi ));

в случае орграфа: – 1, если вершина является началом ребра, 1 – если вершина является концом ребра, и 0 – если вершина является для ребра и началом, и концом (т.е. ребро – петля), проставляется любое

(в каждой строке сумма “+1” и “– 1” равна нулю, т. к. “+1” представляет вершину – исток, а “– 1” вершину – сток, а в каждом столбце матрицы инцидентности количество “+1” равно локальной степени ρ1(vi), а количество “– 1” равно локальной степени ρ2(vi)).

101

– списком рёбер графа, представленным двумя столбцами: в левом перечисляются все рёбра е i Е, а в правом – инцидентные ему вершины vi, vj; для н-графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра:

– матрицей смежности ||δkl|| – квадратичной матрицей размера n 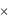n: по вертикали и горизонтали перечисляются все вершины vj V, а на пересечении k-й и l-й вершин в случае н-графа проставляется число, равное числу рёбер, соединяющих эти вершины; для орграфа δkl равно числу рёбер с началом в k-й вершине и концом в l-й.

Если два графа равны, то их матрицы совпадают. Если в н- графе поменять нумерацию вершин, матрицы (и список рёбер) в общем случае изменяются, т.е. вид матриц и списка ребёр зависит от нумерации вершин и рёбер графа.

Пример 5.2. Задать матрицами инцидентности и смежности графы G1 и G2 (см. рисунок 5.2).

Решение:

– матрицы инцидентности (таблицы 5.1, 5.2):

102

Задача 5.1. Граф задан списком рёбер:

103

2)определите степени вершин графа;

3)нарисуйте матрицу инцидентности графа;

2)нарисуйте матрицу смежности графа.

5.2 Операции над частями графа. Графы и бинарные отношения

Граф Н называется частью графа G, Н G, если множества его вершин V(H) и рёбер Е(Н) содержатся в множестве вершин V(G) и рёбер Е(G) соответственно, т.е. V(H) V(G) и Е(Н) Е(G).

Если V(H) = V(G), часть Н графа G называется суграфом.

Суграф Н является покрывающим для н-графа G, если любая вершина графа G инцидентна хотя бы одному ребру из Н.

Подграфом G(V′) графа G(V) с множеством вершин V′ V называется часть, которой принадлежат все рёбра обоими концами из V′.

Над частями графа G могут производиться следующие операции:

– дополнение Н к части Н – определяется множеством всех рёбер

общих вершин V(Н1) V(Н2) = Ø, а значит, и общих рёбер Е(Н1) Е(Н2) = Ø.

Части Н1 и Н2 не пересекаются по рёбрам, если Е(Н1) Е(Н2) = Ø. Если

V(Н1) V(Н2) = Ø, то сумма Н1 Н2 называется прямой.

Графы и бинарные отношения: отношению R, заданному на множестве V, взаимно однозначно соответствует ориентированный граф

G(R) без кратных рёбер с множеством вершин V, в котором ребро (vi, vj) существует, только если выполнено viRvj.

Пример 5.3. Какими особенностями отличается граф G, взаимнооднозначно соответствующий бинарному отношению R, если R:

а) симметрично;

104

б) антисимметрично; в) рефлексивно; г) антирефлексивно; д) транзитивно?

Решение. Пусть бинарное отношение R определено на множестве V

={v1, ..., vn}.

1.Симметричному отношению R взаимно однозначно соответствует

неориентированный граф без кратных рёбер G(R), в котором ребро (vi, vj) существует, если и только если выполнено viRvj (а значит, и vjRvi в силу симметричности R).

2.Антисимметричному отношению R взаимно однозначно соответствует ориентированный граф без кратных рёбер, не содержащий пар вершин с рёбрами, противоположно направленными к разным вершинам.

3.Если R рефлексивно, то граф G(R) без кратных рёбер имеет петли во всех вершинах.

4.Если R антирефлексивно, то граф G(R) без кратных рёбер не имеет

петель.

5.Если R транзитивно, то в графе G(R) без кратных рёбер для каждой пары рёбер (vi, vj) и (vj, vk) имеется замыкающее ребро (vi, vk).

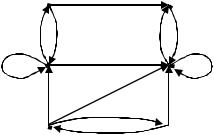
Задача 5.2. Пусть ориентированный граф G на рисунке 5.4 задаёт отношение R : G(R). Каковы свойства отношения?

Рисунок 5.4 – Ориентированный граф G

105

5.3 Маршруты, пути, цепи, циклы. Дерево и лес

Пусть G – неориентированный граф.

Маршрутом в G называется такая последовательность рёбер М(е1, е2,

..., еi, …, en), в которой каждые два соседних ребра еi-1 и еi имеют общую вершину . В маршруте одно и то же ребро может встречаться несколько раз. Начало маршрута – вершина v0, инцидентная ребру е1 и не инцидентная е2; конец маршрута vn инцидентен еn и не инцидентен еn-1. Если е1, е2 (еn-1, еn) – кратные, требуется дополнительное указание, какую из двух инцидентных вершин считать началом (концом) маршрута.

Маршрут, в котором совпадают его начало и конец v0 = vn (т.е. замкнутый), называется циклическим. Маршрут, в котором все рёбра разные, называется цепью. Цепь, не пересекающая себя, т.е. не содержащая повторяющихся вершин, именуется простой цепью.

Циклический маршрут называется циклом, если он является цепью, и простым циклом, когда это – простая цепь.

Вершина vi, vj G называется связанными, если существует маршрут М с началом vi и концом vj. Связанные маршрутом вершины связаны также и простой цепью. Отношение связанности вершин обладает свойством эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества Vi, i = 1, 2, …, k. Граф G называется связным, если все его вершины связаны между собой. Поэтому все подграфы G(Vi) связаны и называются связными компонентами графа. Каждый н-граф распадается единственным образом в прямую сумму своих связных компонент G G(Vi ) .

i

Пусть G – ориентированный граф.

Последовательность рёбер, в которой конец каждого предыдущего ребра еi-1 совпадает с началом следующего еi, называется путём (в нём все рёбра проходят по их ориентации). В пути одно и то же ребро может

106

встречаться несколько раз. Началом пути является начало v0 ребра е1,

концом пути – конец vn ребра еn.

Путь называется ориентированной цепью (или просто цепью), если каждое ребро встречается в нём не более одного раза, и простой цепью, если любая вершина графа G инцидентна не более чем двум его рёбрам.

Контур – путь, в котором v0 = vn. Контур называется циклом, если он является цепью, и простым циклом, когда это – простая цепь. Если граф содержит циклы, то он содержит и простые циклы. Граф, не содержащий циклов, называется антициклическим.

Вершина vj G называется достижимой из вершины vj G, если существует путь L(vi, ..., vj) с началом vi и концом vj.

Орграф G называется связным, если он связен без учёта ориентации дуг, и сильно связен, если из любой вершины vi в любую vj существует путь.

Число рёбер маршрута (пути) называется его длиной.

Расстоянием d(vi, vj) между вершинами vi и vj н-графа G называется минимальная длина простой цепи с началом vi и концом vj. Центром называется вершина н-графа, от которой максимальное из расстояний до других вершин являлось бы минимальным. Максимальное расстояние от центра G до его вершины называется радиусом графа r(G).

Эйлеров цикл – цикл графа, содержащий все рёбра графа. Эйлеров граф – граф, имеющий эйлеров цикл (эйлеров цикл можно считать следом пера, вычёркивающего этот граф, не отрываясь от бумаги).

Теорема Эйлера: конечный неориентированный граф G эйлеров тогда и только тогда, когда он связен и степени всех его вершин чётны.

Эйлерова цепь – цепь, включающая все рёбра данного конечного н-графа G, но имеющая различные начало vi и конец vj. Чтобы в конечном н-графе G существовала эйлерова цепь, необходимы и достаточны его связность и чётность степеней всех вершин, кроме начальной vi и конечной vj (vi и vj должны иметь нечётные степени).

107

Чтобы в конечном орграфе существовал эйлеров цикл, необходимы и достаточны его связность, а также равенство степеней вершин этого графа по входящим и выходящим рёбрам, т.е. p1(v) = p2(v), v G.

Гамильтонов цикл – простой цикл, проходящий через все вершины рассматриваемого графа. Гамильтонова цепь – простая цепь, проходящая через все вершины графа, с началом и концом в разных вершинах х v1, v2 G.

Пример 5.4. Для вершин v1 и v6 графа G на рисунке 5.5 привести примеры маршрута, цепи, простой цепи; определить в графе циклический маршрут, цикл, простой цикл, приняв вершину v1 за их начало и конец.

v4

е3 е4

v3

v5

е2

е5

v7

Рисунок 5.5 – Граф с вершинами v1 и v6

Решение. Для вершин v1, v6 G:

–маршрут, не являющийся цепью – (е1, е2, е3, е4, е5, е1, е8, е7, е6, е1, е8,

е7) или (е1, е2, е3, е4, е5, е1, е8, е7) и т.п.;

–цепь, не являющаяся простой цепью – (е1, е2, е3, е4, е5, е6);

–простая цепь – (е1, е6) или (е8, е7).

Для вершины v1:

–циклический маршрут, не являющийся циклом – (е1, е2, е3, е4, е5, е2,

е3, е4, е5, е6, е7, е8, е1, е6, е7, е8);

–цикл, не являющийся простым циклом – (е1, е2, е3, е4, е5, е6, е7, е8);

–простой цикл – (е1, е6, е7, е8).

108

При описании цикла в качестве его начала и конца может быть выбрана любая вершина, поэтому последовательности (е1, е6, е7, е8), (е6, е7, е8, е1), (е7, е8, е1, е6), (е8, е1, е6, е7) представляют один и тот же цикл. Более того, часто считается, что можно менять порядок рёбер цикла на противоположный, т.е. последовательность (е8, е7, е6, е1) представляет тот же цикл.

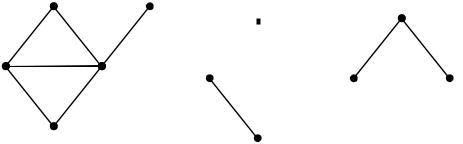
Пример 5.5. Для четырёх графов на рисунке 5.6 определить расстояние между вершинами. Чему равны радиусы графов?

v3

v5 v10

v8

Рисунке 5.6 – Четыре графа

Решение. Пусть G1 – граф с вершинами V1 = {v1, …, v5}; G2 – с вершинами V2 = {v6, v7}; G3 – с вершинами V3 = {v8} и G4 – с V4 = {v9, v10, v11}.

Расстояние d(vi, vj) между вершинами vi и vj как минимальная длина простых цепей с началом vi и концом vj (заметим, что d(vi, vj) = d(vj, vi)):

G1 : d(v1, v5) = 2, d(v1, v4) = 1, d(v3, v5) = 2, и т.д.;

G2 : d(v6, v7) = 1, d(v6, v6) = d(v7, v7) = 0;

G3 : d(v8, v8) = 0;

G4 : d(v9, v10) = 1, d(v9, v11) = 2, d(v10, v11) = 1, d(v9, v9) = 0, и т.д.

Для определения центров и радиусов графов G1 – G4 найдём предварительно для каждого максимальные расстояния r(vi) от вершины vi:

G1 : r(v1) = 2, r(v2) = 2, r(v3) = 2, r(v4) = 1, r(v5) = 2;

109

G2 : r(v6) = 1, r(v7) = 1;

G3 : r(v8) = 0;

G4 : r(v9) = 2, r(v10) = 1, r(v11) = 2.

Отсюда нетрудно определить радиусы r(G) = min r(vi) и центры G:

r(G1) = 1, центр – вершина v4;

r(G2) = 1, центры – обе вершины v6, v7;

r(G3) = 0, центр – вершина v8;

r(G4) = 1, центр – вершина v10.

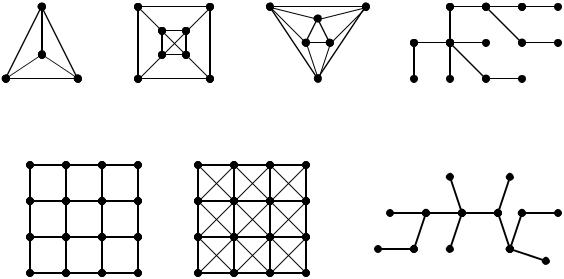
Задача 5.3. Построить матрицы смежности си инцидентности графов G1 – G10 (рисунок 5.7). Чему равны степени вершин? Имеют ли графы эйлеров цикл (цепь)? Какому отношению соответствует каждый граф (задать отношение матрицей, определить свойства отношения)? Каковы расстояния между вершинами в графах G1 – G7? Какие вершины графов являются центрами? Каковы радиусы этих графов?

110