
5543
.pdf
Так как отношения на М задаются подмножествами, R M1 M 2
(или R M 2 , если М1 = М2 = М), для них определены те же операции, что
инад множествами.
1.Объединение R1 R2 :
|
R1 |
R2 |
(a, b) |
|
(a, b) |
R1 или (a, b) R2 . |
|
||||||
2. |
Пересечение R1 |
R2 : |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
R1 |
R2 |
(a, b) |
(a, b) R1 и (a, b) R2 . |
|
||||||||
3. |
Разность R1 \ R2 : |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
R1 \ R2 |
(a, b) |
(a, b) R1 и (a, b) R2 . |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Дополнение R : |
|
|
|
|
|
|
|
|
||||
|
|
|
|
U \ R , где U = М1 |
М2 (или U = М2). |
|
|||||||
|
|
R |
|
||||||||||
Кроме того, определяют другие операции над отношениями, в том |
|||||||||||||
числе : |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Обратное отношение R-1: |
|
|
|
|
||||||||
aR-1b тогда и только тогда, когда bRa: R 1 (a, b) |
|
(b, a) |
R . |
||||||||||
|
|||||||||||||
Например, если R – «Быть моложе», то R-1 – «Быть старше», если R – |
|||||||||||||
«Быть сыном», то R-1 – «Быть отцом (или матерью)». |
|
||||||||||||
6. |
Составное отношение (композиция) R1 R2 . |
|
|||||||||||
Пусть заданы множества М1, М2, |
М3 и отношения R1 |
M1 M 2 и |
|||||||||||
R2 |
M 2 |
M 3 . Составное отношение действует из М1 в М2 посредством |
|||||||
R1, |
а затем из М2 |
в М3 посредством R2, т.е. (a, b) |
R1 R2 , если существует |
||||||
такое c |
M 2 , что (a, c) |
R1 и (c, b) |
R2 . |
|
|||||
|
В |
частности, если |
отношение R определено на множестве М, |
||||||
R |
M 2 , то составное отношение |
|
|
||||||
|
|
|
R R (a, b) |
(a, c), (c, b) |
R . |
||||
|
Например, если R – «Быть сыном», то R R – «Быть внуком». |
||||||||
|
Обозначим |
R R |
R(2) . Используя это обозначение, можно |
||||||
определить R(n) для любого n N , n > 1 следующим образом: |
|||||||||
|
|
|
R(n) |
|
|
R(n 1) . |
|||
|
|
|
(a, b) |
(a, c) |
R и (c, b) |
||||
21

7. Транзитивное замыкание R0.
Транзитивное замыкание R0 состоит из таких и только таких пар элементов a, b из М, т.е. (a, b) R0 , для которых в М существует цепочка из (k + 2) элементов М, k ≥ 0: a, c1, c2, …, ck, b, между соседними элементами которой выполняется R: aRc1, c1Rc2, …, ckRb, т.е.:
R0 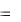 (a, b) (a, c1), (c1, c2 ), ..., (ck , b) R .
(a, b) (a, c1), (c1, c2 ), ..., (ck , b) R .
Унарная операция транзитивного замыкания R0 может быть также определена как бесконечное объединение:
R0 |
R R(2) R(3) |
... R(n) ... |
Например, для соотношения R – «Быть сыном» составное отношение |
||
(композиция) R R |
R(2) – «Быть |
внуком», R R R R(3) – «Быть |
правнуком» и т.д. Тогда объединение всех этих отношений есть транзитивное замыкание R0 – «Быть прямым потомком».
Если отношение R транзитивно, то R0 = R. Например, транзитивное замыкание отношения R – «Быть больше» совпадает с этим отношением, т.е. R0 = R.
8. Рефлексивное замыкание R*.
Пусть тождественное отношение Е 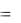 (a, а) a М . Тогда если R
(a, а) a М . Тогда если R
транзитивно и рефлексивно, то R* = R.
Пример 1.10. Пусть отношение R – «Быть руководителем», определённое на множестве сотрудников организации М. Назовите отношения: R , R-1, R0, R*.
|
|
|
|
||
Решение. R |
(М М ) \ R – «Не быть руководителем»; |
||||
R 1 |
(b, a) | (a, b) |
R – «Быть подчинённым»; |
|||
R0 = R – «Быть руководителем» (так как R – транзитивно); |
|||||
R* |
R0 E |
R |
E – трудно назвать такое отношение, возможно – |
||
«Быть руководителем, в том числе по отношению к самому себе».
Пример 1.11. Пусть на множестве М = {2, 4, 6} определено отношение R – «Быть меньше». Задайте характеристическим свойством и списком отношение R, обратное отношение R-1 и дополнение R . Сравните отношения. Определите их свойства.
22

Решение. R |
|
(a, b) |
a |
b – «Быть меньше». |
||
R = {(2, 4), (2, 6), (4, 6)}. |
|
|
|
|||
R 1 (a, b) |
|
(b, a) |
R |
(a, b) |
|
a b – «Быть больше». |
|
|
|||||
R-1 = {(4, 2), (6, 2), (6, 4)}.
R (М М ) \ R 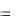 (a, b) (a, b) R
(a, b) (a, b) R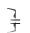 (a, b) a b – «Быть не меньше».
(a, b) a b – «Быть не меньше».
R = {(2, 2), (4, 2), (4, 4), (6, 2), (6, 4), (6, 6)}.
Между R, R-1 и R имеют место соотношения:
|
|
|
R 1 |
|
R 1 |
|
E Ø, |
||||
|
R |
E; |
|
||||||||
где Е |
(a, b) |
|
a |
b |
– тождественное отношение; |
||||||
|
|||||||||||
|
|
|
|
|
R 1 |
|
|
||||
R R U , R |
E |
U , |
|||||||||
где U = М М; |
|
|
|||||||||
|
|
|
|
Ø, R |
|
R 1 |
Ø, R E Ø. |
||||
R |
|
R |
|
||||||||
Отношения R и R-1 – антирефлексивны, антисимметричны, транзитивны, т.е. являются отношением строгого порядка. Эти отношения задают полный порядок на множестве М.
Отношение R – рефлексивно, антисимметрично, транзитивно, т.е. является отношением нестрогого порядка; оно также задаёт полный порядок на множестве М.
Задача 1.13. Назвать отношения R , R-1, R(2), R0, R*, если отношение R означает:
а) «Быть братом»; б) «Быть сыном»;
в) «Жить в одном городе».
Задача 1.4. Пусть на множестве М = {1, 2, 3, 4} определено отношение R – «Быть больше». Выполнить операции над отношением R; задать полученные в результате операций отношения характеристическим свойством, списком, а также назвать отношения. Сравнить отношения; определить их свойства.
23
1.4 Соответствия
Соответствие – способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями).
|
Соответствием между множествами А и В называется |
||||||
подмножество G прямого произведения этих множеств: G |
A B . Если |
||||||
(a, b) G , то говорят, что «b соответствует a при соответствии G». |
|||||||
|
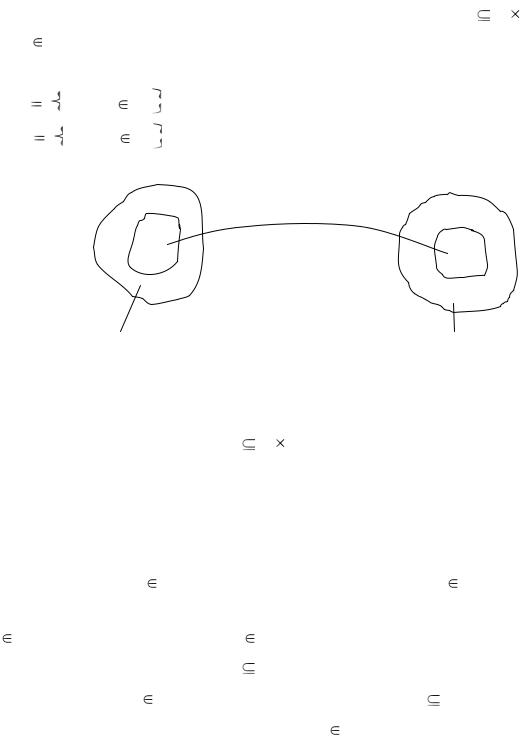
Область |
определения |
соответствия |
G |
– |
множество |
|
|
|
|
G . Область значений соответствия G – |
множество |
|||
np1G |
a |
(a, b) |
|||||
|
|
G (рисунок 1.8). |
|
|
|
|
|
np2G |
b |
(a, b) |
|
|
|
|
|
|
|
А |
|
G |
|
|
B |
|
|
|
|
|
|
|
|
а |
b |
|
np1G |
np2G |
Рисунок 1.8 – Область соответствия и область значений |
|
Свойства соответствий G |
A B : |
1. Всюду (полностью) определённое соответствие – если np1G = A.
Частично определённое соответствие – в противном случае. 2. Сюръективное соответствие – если np2G = В.
Образом элемента а в множестве В при соответствии G называется множество всех b В , соответствующих элементу a А. Прообразом элемента b в множество А при соответствии G называется множество всех a А, которым соответствует b В .
Образом множества С np1G называется объединение образов всех элементов a C . Прообразом множества D np2G называется объединение прообразов всех элементов b D .
24
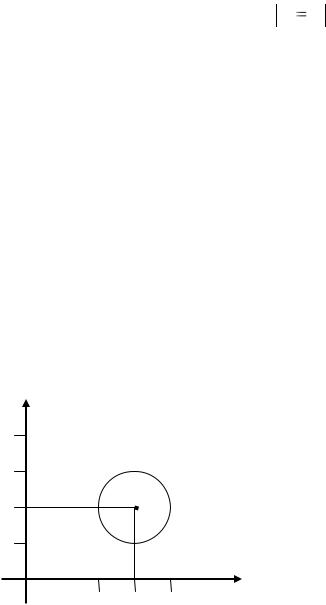
3.Функциональное (однозначное) соответствие – если образом любого элемента а из области определения np1G является единственный элемент b из области значений np2G.
4.Взаимно-однозначное соответствие – если оно:
а) всюду определено; б) сюръективно; в) функционально;
г) прообразом любого элемента b из области значений np2G является единственный элемент а из области определения np1G.
Если между множествами А и В существует взаимно однозначное соответствие, то мощности этих множеств равны, т.е. А
 В . В таком случае говорят, что множества А и В равномощны. Этот факт позволяет:
В . В таком случае говорят, что множества А и В равномощны. Этот факт позволяет:
–установить равенство мощностей двух множеств, не вычисляя этих множеств;
–вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется.
Множества, равномощные множеству натуральных чисел N, называются счётными.
Пример 1.12. Пусть G – множество всех пар действительных чисел (х, у), удовлетворяющих соотношению (х – 3)2 + (у – 2)2 ≤ 1. Графически такое соответствие G представляет собой круг радиуса 1 с центром в точке (3; 2). Таким образом, круг G задаёт соответствие между R и R (осью абсцисс и осью ординат, рисунок 1.9).
у
4
3 |
G |
2
1
|
|
2 |
3 |
4 |
х |
|
|
||||
1 |
|
||||
Рисунок 1.9 – Соответствие между R и R
25
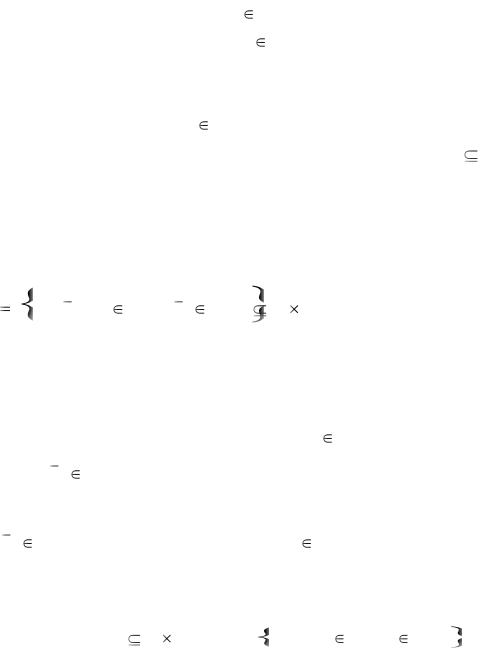
Определите, чему равны образы и прообразы чисел 2, 3, 4.
Решение. Образом числа 2 np1G (на оси абсцисс) при соответствии G является единственное число 2 np2G (на оси ординат). Образ числа 3 при соответствии G есть множество всех действительных чисел отрезка [1, 3], а образ числа 4 – число 2.
Прообразом числа 2 np2G (на оси ординат) при соответствии G будет множество всех действительных чисел отрезка [2, 4] np1G (на оси абсцисс), прообразом числа 3 при соответствии G – число 3, а прообраза числа 4 при соответствии G не существует.
Пример 1.11. Каковы свойства соответствия между множеством N натуральных чисел и множеством M2n степеней двойки:
G (n, 2n 1) |
n N, 2n 1 M |
2 |
n |
N M |
2 |
n ? |
|
|
|
|
|
||
|
|
|
|
|
|
|
Решение. Соответствие G взаимно однозначно:
–всюду определено, так как np1G = N;
–сюръективно, поскольку np2G = M2n ;
–функционально, так как любому n N соответствует единственный
образ 2n 1 M |
2 |
n ; |
|
|
– характеризуется единственностью прообраза, так как для любого
2n 1 M |
2 |
n существует единственное n N. |
|
|
Задача 1.14. Каковы свойства соответствия G между множеством N натуральных чисел и множеством M 2n натуральных чётных чисел:
G N M 2n ; G 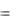 (n, 2n) | n N , 2n M 2n .
(n, 2n) | n N , 2n M 2n .
1.5 Функции и отображения
Функцией называется функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип А → В (обозначается f : А → В).
Каждому элементу а из области определения функция f ставит в соответствие элемент b из области значений. Это обозначается f(a) = b. Элемент а – аргумент функции, элемент b – значение функции на а.
26

Отображением А в В называется всюду определённая функция f : А → В. Отображением А на В называется всюду определённое при этом сюръективное функциональное соответствие f : А → В.
Отображение типа А → А часто называют преобразованием множества А. Функция типа А → А, являющаяся отображением А на А,
называется перестановкой на А. Функции f и g равны, если:
–их области определения – одно и то же множество А;
–для любого а А f(a) = g(a).
Функция типа f : A1 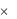 A2
A2 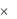 …
… 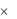 An → В называется n-местной. В этом случае принято считать, что функция имеет n аргументов: f(a1, …, an)
An → В называется n-местной. В этом случае принято считать, что функция имеет n аргументов: f(a1, …, an)
= b, где а1 А1, ..., аn Аn, b B. |
|
|
Пусть дано соответствие G A B . Тогда соответствие H B |
A |
|
называется обратным к G (обозначается |
G-1). Если Н таково, |
что |
(b, a) H тогда и только тогда, когда (a, b) |
G . |
|
Если соответствие, обратное к функции f : А → В, является функциональным, то оно называется функцией, обратной к f (обозначается f--1). Для функции f : А → В обратная функция существует тогда и только тогда, когда f является взаимно однозначным соответствием между своими областями определения и значений.
Пусть даны функции f : А → В и g : B → C. Функция h : А → С называется композицией функции f и g (обозначается f ◦ g), если имеет место равенство
h(x) = g(f(x)), где х А.
Часто говорят, что функция h получена подстановкой f в g. Для многоместных функций f : Аm → В, g : Bn → C возможны различные варианты подстановки f в g, дающие функции различных типов. Например, при m = 3 и n = 4 функция h = g(x1, f(y1, y2, y3), x3, x4) имеет шесть аргументов и тип В 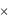 А3
А3 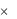 В2 → С.
В2 → С.
Функция, полученная из f1, ..., fn некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией f1, ..., fn. Выражение, описывающее эту суперпозицию и содержащее
27

функциональные знаки и символы аргументов (и, разумеется, скобки), называется формулой.
Способы задания функции:
–графиком;
–таблицей;
–формулой, описывающей функцию как суперпозицию других (исходящих) функций;
–рекурсивной вычислительной процедурой. Например, функция f(x) = 1 ∙ 2 ∙ 3 ∙ ... ∙ (х – 1) ∙ х = х! описывается рекурсивной вычислительной процедурой, задаваемой следующими правилами:
1) f(0) = 1; 2) f(x + 1) = f(x) ∙ (х + 1).
Пример 1.12. Таблица выигрышей лотереи устанавливает соответствие G между парами чисел из N 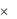 N = N2 (серия, номер выигравшего билета) и множеством выигрышей М, т.е. G
N = N2 (серия, номер выигравшего билета) и множеством выигрышей М, т.е. G 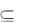 N2
N2 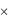 М. Является ли заданное соответствие функцией?
М. Является ли заданное соответствие функцией?
Решение. Соответствие G 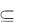 N2
N2 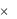 М, задаваемое таблицей выигрышей, является функциональным, так как для каждой указанной пары из N2 (серии, номера билета) определён конкретный (единственный) выигрыш из М. Таким образом, данное соответствие есть двухместная функция f: N
М, задаваемое таблицей выигрышей, является функциональным, так как для каждой указанной пары из N2 (серии, номера билета) определён конкретный (единственный) выигрыш из М. Таким образом, данное соответствие есть двухместная функция f: N 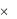 N → M. Функция такого типа не всюду определена, значит не является отображением. Более того, как правило, число выигравших билетов (мощность области определения np1f) больше перечня наименований выигрышей (мощность области значений np2f), поэтому данная функция не обладает единственностью прообраза. В силу
N → M. Функция такого типа не всюду определена, значит не является отображением. Более того, как правило, число выигравших билетов (мощность области определения np1f) больше перечня наименований выигрышей (мощность области значений np2f), поэтому данная функция не обладает единственностью прообраза. В силу
сказанного f не является взаимно однозначным соответствием.
Пример 1.13. Функции f и g имеют тип f : А3 → В, g: В4 → С. Какой тип имеют функции h1 и h2, являющиеся композициями f и g:
|
|
а) h1 = g(x1, f(y1, y2, y3), x3, x4); |
||
|
|
б) h2 = g(f(y1, y2, y3), f(z1, z2, z3), x3, x4)? |
||
|
|
Решение. Функция h1 |
содержит шесть аргументов и её тип |
|
h1: |
В |
А3 |
В2 → С. Функция h2 содержит восемь аргументов, её тип |
|
h2: |
А3 |
А3 |
В2 → С или h2: А6 |
В2 → С. |
28
Задача 1.15. Функции f и g имеют тип f : А2 → В, g: В5 → С. Какой тип имеют функции h1 и h2, являющиеся композициями f и g:
а) h1 = g(х1, f(y1, y2), f(z1, z2), x4, x5); б) h2 = g(х1, х2, f(y1, y2), x4, f(z1, z2));
в) h3 = g(f(y1, y2), x2, f(z1, z2), f(u1, u2), x5)?
Глава 2. БУЛЕВА АЛГЕБРА
Формальная логика в своём развитии прошла два основных этапа. Основанием деления на эти этапы служит различие применяемых в логике средств и методов исследования. Начало первого этапа связано с работами древнегреческого философа и учёного Аристотеля (384 – 322 гг. до н.э.), в которых впервые дано систематическое изложение логики. Логику Аристотеля и всю доматематическую логику обычно называют «традиционной» формальной логикой.
Второй этап – это появление математической (или символической) логики. Немецкий философ Г. В. Лейбниц (1646 – 1716 гг.) по праву считается основоположником математической (символической) логики.
Начиная с Лейбница в логике используется в качестве метода исследования метод формализации, который традиционной логикой относился только к методам математического исследования, а Лейбниц показал, что он имеет общенаучный характер.
Математическая (или символическая) логика делится на три подраздела: логику Буля, логику высказываний и логику предикатов.
«Логика Буля» основывается на отношении эквивалентности, при котором правая часть равенства всегда содержит ровно столько же «истины», сколько и левая. Строго говоря, в этом случае не происходит приращения нового знания. Два последующих подраздела, «Логика высказываний» и «Логика предикатов», базируется уже на отношении порядка, при котором правая часть выражения (заключение) содержит больше «истины», чем левая (посылки), т.е. «истинность» заключения
29
оказывается выше «истинности» посылок, о чём можно судить, в частности, по количеству единиц в таблице истинности.
2.1 Операции логики Буля
Операции булевой логики удобно ввести используя аналогии с операциями над множествами. Будем рассматривать только счетные множества, т.е. для которых установлено взаимно однозначное соответствие с числами натурального ряда.
Пусть задано некоторое множество U – универсальное множество. Множества А, В – подмножества U. Для удобства будем считать, что элементы множества А обладают свойством А, а элементы множества В – свойством В. В результате получим четыре класса элементов (рисунок 2.1):
С0 – множество, элементы которого не обладают ни свойством А, и свойством В;
С1 – множество, элементы которого обладают только свойством А; С2 – множество, элементы которого обладают только свойством В; С3 – множество, элементы которого обладают одновременно и
свойством А и свойством В.
|
|
U |
|
|
|
|
|
|
А |
В |
|
|
А |
В |
|
|
|
С3 |
|
|
|
|
|
|
С1 |
С2 |
|
|
|
|
|
|
|
С0 |
|
|
|
|
|
|
|
|
|
|
|
||
Рисунок 2.1 – Четыре класса |
Рисунок 2.2 – Три класса |
||||||
|
элементов |
|
элементов |
||||
Рассмотрим сначала операцию объединения. Объединением охватываются три класса элементов С1, С2, С3 (рисунок 2.2). Логически операцию объединения двух множеств можно охарактеризовать словами: «элемент х принадлежит множеству А или множеству В». При этом союз или одновременно означает и союз и.
x A B (x A) (x B),
30
