5543

где 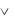– символ логической связки или, которая называется дизъюнкцией.

С точки зрения логики, вместо одной переменной х удобно ввести две логические переменные х1 и х2. Областью определения х1 и х2 будут два логических значения: 1 – для истинного значения и 0 – для ложного.

Переменные х1 и х2 определяют некоторую логическую функцию у = f(х1, х2), которая в случае дизъюнкции может быть записана как

Между таблицей истинности и диаграммой Эйлера – Вена существует взаимно однозначное соответствие. Поэтому число единиц для у всегда будет совпадать с числом заштрихованных областей на диаграмме.

Пересечению множеств А и В соответствует класс С3. Тот факт, что х принадлежит одновременно двум множествам А и В, можно представить выражением:

х А В (х А) (х В),

где 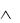– символ логической связки и, которая называется конъюнкцией. Если в таблице истинности для дизъюнкции все нули заменить

единицами, а все единицы – нулями, то в итоге получим таблицу истинности для конъюнкции (таблица 2.2). Этот факт определяет взаимную двойственность конъюнкции и дизъюнкции.

31

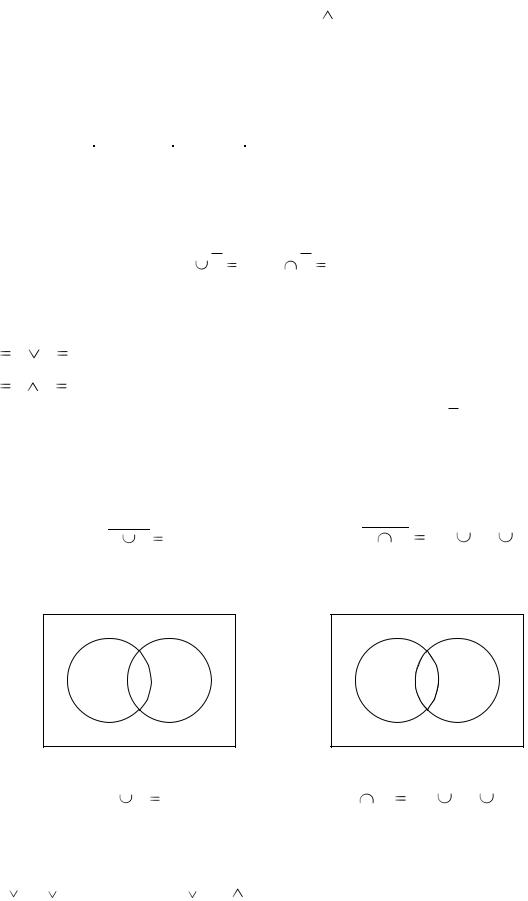
Таблица 2.2 – Таблица истинности для конъюнкции

Для любой логической операции можно найти двойственную.

Для любого подмножества А и универсального множества U выполняются тождества

АА U, А А Ø.

Аналогичные равенства выполняются и для логических функций, которые имеют соответствующие названия:

Дополнение к любой логической переменной х, т.е. x (не х), называется в логике отрицанием х.

Тавтология – это всегда истинное логическое выражение. Противоречие, напротив, всегда ложное выражение.

Для классов А В С0 (рисунок 2.3) и А В С0 С1 С2

(рисунок 2.4) вводят новые операции, которые соответственно называют

стрелка Пирса (или функция Вебба) и штрих Шеффера:

32

(х1 х2) 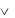(х1 | х2) = 1, (х1 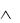х2) 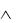(х1 | х2) = 0.

Из таблиц истинности для этих операций (таблицы 2.3 и 2.4) видно, что

Разности множеств А и В (рисунок 2.5) А \ В = С1 соответствует логическая функция у = х1 – х2 (таблица 2.5), её дополнением служит

импликация (таблица 2.6):

Рисунок 2.5 – Разность множеств А и В

Симметрическая разность (строгая дизъюнкция, сумма по модулю два)

двух множеств А и В (рисунок 2.6) есть объединение двух разностей (таблица 2.7).

33

Рисунок 2.6 – Симметрическая разность множеств А и В

Таблица 2.7 – Объединение двух разностей

Эквивалентность (рисунок 2.7) определяется теми элементами множеств А и В, которые для них являются общими. Однако элементы, не входящие ни в А, ни в В, также считаются эквивалентными (таблица 2.8).

А В

Рисунок 2.7 – Эквивалентность

Таблица 2.8 – Эквивалентные элементы

Из условия дополнительности операций вытекают следующие соотношения:

34

Заметим: функции пронумерованы так, что номер функции, записанный в двоичной системе счисления, даёт последовательность значений соответствующей функции. Например, двоичная запись числа 13 имеет вид: 1101. Соответствующая функция f13(a, b) принимает следующие значения: f13(0, 0) = 1, f13(0, 1) = 1, f13(1, 0) = 0, f13(1, 1) = 1.

2.2 Формы представления булевых функций

Любую булеву функцию у = f(a, b) можно представить как некоторую комбинацию областей:

С0 a b, C1 a b, C2 a b, C3 a b.

Тогда, в зависимости от значения функции и заданных Сi, которые в этом случае будем называть конституентами, получим шестнадцать логических операций в виде:

y a b f (0, 0) a b f (1, 0) a b f (0, 1) a b f (1, 1) ,

то есть любую булеву функцию можно представить как дизъюнкцию элементарных конъюнкций всех переменных (с отрицаниями или без них) и значений этой функции на соответствующем конкретном наборе значений переменных.

Подобная форма представления логических функций называется

совершенной дизъюнктивной нормальной формой (СДНФ).

В логике Буля действует принцип двойственности, который гласит: при одновременной замене символов 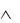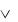 и 1 0, все логические равенства остаются в силе. Поэтому нашу СДНФ можно представить несколько иначе:

y 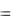a b f (1, 1) a b f (0, 1) a b f (1, 0) a b f (0, 0) .

Эта форма представления называется совершенной конъюнктивной нормальной формой (СКНФ).

В таблице 2.10 приведён полный список элементарных логических функций от двух аргументов в двух совершенных формах – СДНФ и СКНФ.

36

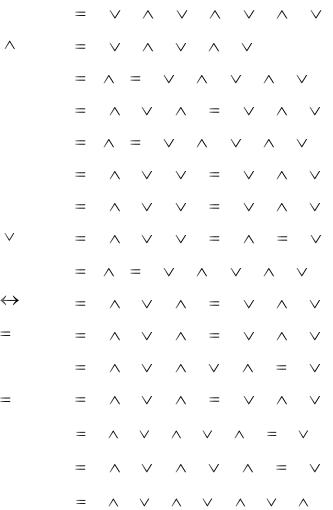
Таблица 2.10 – Элементарные логические функции

Совершенные формы представлений позволяют выразить аналитической формулой любую функцию, если известна её таблица истинности.

Пример 2.2. Представить в явном виде функцию, зависящую от трёх элементов, заданную таблицей истинности (таблица 2.11).

Таблица 2.11 – Таблица истинности

37

Решение. Выписывая соответствующие конъюнкты против единичных значений у, мы получаем СДНФ. Если же выпишем дизъюнкты против нулевых значений у, то в результате получим СКНФ.

В логике Буля действует закон склеивания:

(a b) (a b) a, (a b) (a b) a.

Применение этих законов позволяет найти более компактные аналитические выражения для заданной функции у, т.е. минимальную дизъюнктивную нормальную форму уМДНФ и минимальную конъюнктивную нормальную форму уМКНФ. Приведём соответствующие формы представления функции у, заданной таблицей 2.11:

уМДНФ (х3 х1) (х2 х1) (х3 х2 х1),

уМКНФ (х3 х1) (х3 х2 х1) (х2 х1).

Переменные хi и хi часто называют термами. Именно полный набор из n термов образует конституенту. В процессе же минимизации некоторые термы из конституент пропадут. Тогда оставшуюся часть дизъюнкта или конъюнкта называют импликантой.

Обращаем внимание на то, что одну и ту же конституенту (импликанту) можно склеивать с другими конституентами (импликантами) многократно, так как в логике Буля действует закон идемпотентности: a a a a a a ..., a a a a a a ..., поэтому любую конституенту можно размножать.

2.3Методы доказательств в логике Буля

Вкачестве основных законов логики Буля чаще других называют:

38

Не все восемь законов независимы друг от друга. Так, например, закон идемпотентности можно получить из закона поглощения с использованием закона дистрибутивности:

a a (a b) (a a) (a b) (a (a b)) (a (a b)) a a.

Закон поглощения может быть выведен из закона нуля и единицы: a (a b) (a 1) (a b) a (1 b) a 1 a.

При доказательствах логических выражений мы всегда должны иметь в виду принцип двойственности.

Вкачестве независимой системы законов можно взять законы коммутативности, ассоциативности, дистрибутивности, нуля и единицы.

Влогике широко используются два подхода – аксиоматический и конструктивный. При аксиоматическом доказательстве используется жёсткая система аксиом, состоящая, например, из четырёх только что названных. Все остальные тождества нужно представлять через эти законы. При конструктивном же доказательстве мы должны воспользоваться системой конструктов, примерами которых являются диаграммы Эйлера – Вена и таблицы истинности.

Для доказательства тождества а 0 0 приверженец аксиоматического подхода приведёт примерно такую цепочку преобразований:

а 0 а (а а) (а а) а ((а а) 0) а ((а а) (а а)) а 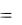(а (а а)) а (а 1) а а а 0.

И сделает он это только ради того, чтобы формально привязаться к провозглашённой ранее системе аксиом. В то же время для конструктивиста исходное тождество не требует никаких доказательств.

39

Картина выглядит противоположным образом в отношении, например, закона дистрибутивности. Аксиоматик в данном случае не предпринимает никаких действий, а сторонник конструктивного подхода обязан продемонстрировать эквивалентность правой и левой части тождества:

а (b c) (a b) (a c).

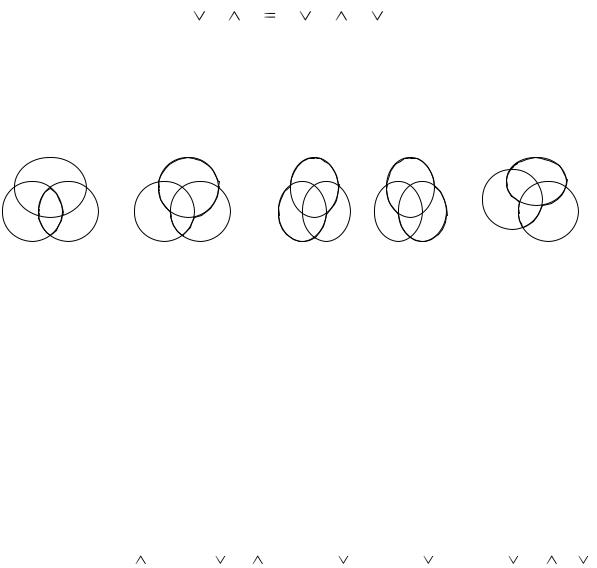
Проведём доказательство с помощью диаграмм Эйлера – Вена (рисунок 2.8). С этой целью построим две диаграммы, которые отвечают двум операциям левой части и три диаграммы, отвечающие трём операциям правой части тождества:

Рисунок 2.8 – Диаграммы Эйлера – Вена

Как видно из диаграмм, результаты построения логических операций левой и правой частей закона дистрибутивности полностью совпали.

В правильности тождества можно убедиться и с помощью таблицы истинности.

Для доказательства построим таблицу 2.12. Она показывает, что наборы значений из нулей и единиц для левой части (fL) совпали с наборами правой части (fR), значит исходное тождество верно.

Таблица 2.12 – Проверка на правильность исходного тождества

40