
Сандракова Дифферентсиалные формы на гладкикх многообразиякх 2014
.pdf
Определение 5.7. Группа πn ( X ) называется n-мерной гомото-
пической или n-й гомотопической группой.
Покажем, что на множестве πn ( X ) можно ввести групповую структуру.
Пусть заданы отображения ϕ, ψ: S n → X . Требуется опреде-
лить их композицию ψϕ: |
S n → X . Пусть сфера S n задана урав- |
|||
нением |
|
|
|
=1 в Rn+1 . |
S n : x2 |
+ x2 |
+... + x2 |
||
0 |
|
1 |
n |
|
Рассечем сферу экваториальной плоскостью x0 = 0 . Будем считать, что отмеченная точка лежит в экваториальной плоскости. Отображение ψϕ: S n → X устроено следующим образом.
Нижняя половина сферы S n пред- |
|
ставляет собой диск Bn . После факто- |
|
ризации Bn по экваториальной сфере |
|
S n−1 получаем сферу S n . Эту сферу |
|
отображаем в X по правилу ϕ (эквато- |
|
риальная сфера при этом отображается |
|
в отмеченную точку). На верхней по- |
|
ловине сферы отображение задаем по |
|
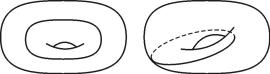
правилу ψ (рис. 8). Полученное ото- |
Рис. 8 |
бражение непрерывно, так как отобра- |
|
жения ϕ и ψ согласованы на том мно- |
|
жестве, на котором они оба определе- |
|
ны. А именно экваториальную сферу |
|
S n−1 они отображают в отмеченную точку.
Следствие 5.1. Множество всех отображений
(S n ; a0 ) → ( X ; x0 )
для любого топологического пространства X совпадает с множеством всех отображений Bn → X , переводящих всю граничную сферу S n−1 = ∂Bn в точку x0 .
Теорема 5.1. При n >1 группа πn ( X ) коммутативна.
111

Доказательство.
1. Пусть n = 2 . Отображения ϕ: S 2 → X ,
ψ : S 2 → X являются представителями двух классов эквивалентности элементов группы π2 ( X ) . Отображение ψϕ: S 2 → X можно
представить как отображение B2 → X , где
диск B2 состоит из двух полудисков и на одном из полудисков задано отображение ϕ, а на другом отображение ψ. Граница каждого полудиска отображается в отмеченную точку x0
Рис. 9 (рис. 9, а). Будем вращать разделяющий полудиски диаметр (рис. 9, б).
Для любого угла α обозначим через Lα отображение B2 → B2 ,
заданное поворотом на угол α вокруг центра диска. Затем для любого α [0; π] обозначим через ψϕα отображение, совпадающее с
ϕ L−α с одной стороны от повернутого диаметра, и ψ L−α – с
другой. После поворота на угол π отображения ϕ и ψ поменяются местами, т.е.
ψϕα = ϕψα .
Таким образом, получаем однопараметрическое семейство отображений, связывающих ψϕ с ϕψ .
2. При n > 2 доказательство точно такое же.
Получаем набор топологических инвариантов πn ( X ) : у гомео-
морфных пространств гомотопические группы изоморфны. Все множества Π( A, X ) образуют более широкий набор топологических
инвариантов. Но если Π( A, X ) – просто множество, без какой-либо
алгебраической структуры, то это очень слабый инвариант. Существуют негомеоморфные топологические пространства,
которые не различаются инвариантами Π( X ; A) и Π( A, X ) . Во
многих случаях полезнее другое отношение эквивалентности: не гомеоморфности, а гомотопической эквивалентности.
Определение 5.8. Топологические пространства X и X ′ называются гомотопически эквивалентными, если существуют такие не-
112

прерывные отображения f : X → X ′ и g : X ′ → X , что их композиции gf и fg гомотопны тождественным отображениям. Отобра-
жения f и g при этомназываются гомотопической эквивалентностью. Гомеоморфные пространства гомотопически эквивалентны. Об-
ратное, вообще говоря, неверно.
Пример 5.2. Цилиндр I ×S1 и окружность S1 гомотопически эквивалентны (рис. 10). Отображение f : S1 → I ×S1 задается как гомеоморфизм f : S1 →{0}×S1 I ×S1 , а отображение g : I × S1 → S1 задается как проекция цилиндра на нижнее основание {0}×S1 и гомеоморфизма f −1 .
Рис. 10
Утверждение 5.1. Если топологические пространства X и X ′ гомотопически эквивалентны, то их гомотопические группы изоморфны, а множества Π( A; X ) и Π( A; X ′) находятся в естествен-
ном взаимно однозначном соответствии, равно как и множества
Π( X ; A) и Π( X ′; A) .
(Доказать самостоятельно.)
Зависимость от отмеченной точки. При определении гомотопических групп выделялась отмеченная точка. Что будет, если выберем другую отмеченную точку? При этом пространство X считается линейно связным. Для несвязного пространства нужно отдельно рассматривать его компоненты линейной связности. Существует способ отождествлять π1 ( X ; x0 ) с π1 ( X ; x0′) , но это отождествление неод-
нозначно. Под отождествлением понимается построение изоморфизма. Изоморфизм между группами строится так: возьмем путь, соединяющий точку x0 с точкой x0′ . Петле с начальной точкой x0′
113
поставим в соответствие петлю с начальной точкой x0 , которая устроена так: первая ее треть – путь l от x0 до x0′ , вторая треть – петля в x0′ , последняятреть – обратный путь l−1 из x0′ в x0 .
§23. Примеры гомотопически эквивалентных пространств
1.Для любого топологического пространства X
X и I × X
гомотопически эквивалентны.
2.Лист Мебиуса гомотопически эквивалентен S1 .
3.Топологическое пространство GL(Rn ) ≡ GL(n, R) (множество матриц размером n×n с ненулевым определителем) гомотопиче-
ски эквивалентно топологическому пространству O(Rn ) ≡ O(R, n)
(множество ортогональных матриц порядка n).
4. Топологическое пространство SL(n, R) матриц с определите-
лем, равным 1, гомотопически эквивалентно SO(Rn ) ≡ SO(n, R) (ортогональные матрицы с определителем, равным 1).
114

Г л а в а 6
РАССЛОЕНИЕ ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА
§ 24. Накрытие
Определение 6.1. Пусть X, Y – топологические пространства. Отображение
p : X → Y ,
где Y линейно связно, называется накрытием, если у любой точки y Y существует такая окрестность U, что ее полный прообраз
p−1 (U ) гомеоморфен некоторому количеству экземпляров U, т.е. p−1 (U ) ≈U × ,
где – дискретное топологическое пространство. Причем этот гомеоморфизм согласован с отображением p в том смысле, что естественная проекция на сомножитель
U × →U
совпадает с отображением p, т.е. диаграмма p−1 (U ) ≈U ×Δ
2 |
0 |
|
U |
коммутативна. Если состоит из k точек, то накрытие называется k-листным.
Примеры накрытий.
1. S n → RPn .
2. S1 ={z ^; z =1} → S1 , z → zk .
3.R1 → S1 , t → cos t + i sin t .
4.Накрытие грассманианов.
115
Определение 6.2. Многообразием Грассмана Gk (Rn ) называет-
ся множество всех k-мерных подпространств в Rn .
Определение 6.3. Ориентированным многообразием Грассмана Gk+ (Rn ) называется множество всех k-мерных подпространств в
Rn с заданными на них ориентациями.
Пример.
1.G1 (Rn ) = RPn−1 .
2.G1+ (Rn ) ≈ Sn−1 .
3.Gn−1(Rn ) ≈ RPn−1 .
4.Gn−k (Rn ) ≈ Gk (Rn ) , k =1, 2, ..., n −1 .
Последнее отождествление определяется любой невырожденной билинейной формой в Rn . А отождествление
Gk+ (Rn ) ≈ Gn+−k (Rn )
зависит еще и от выбора ориентации. |
G+ (Rn ) ≈ G (Rn ) |
|
|
Имеется двулистное накрытие |
(забывание |
||
|
k |
k |
|
ориентации), это накрытие обобщает накрытие S n−k → RPn−1 . |
|||
Из условия линейной связности базы Y накрытия |
p : X → Y , |
||
следует, что дискретное множество |
одно и то же для всех точек |
||
y Y , т.е. y1 , y2 Y |
имеется взаимно однозначное соответствие |
||||
между множествами |
( y1 ) |
и |
( y2 ) , где |
|
|
( y ) ≈ p−1 |
( y ) и ( y ) ≈ p−1( y |
2 |
) . |
||
1 |
|
1 |
2 |
|
|
Соединим точки y1 , y2 Y |
каким-нибудь путем. Покроем этот путь |
||||
окрестностями, участвующими в определении накрытия. Из этого покрытия открытыми множествами компактного множества можно выделить конечное подпокрытие. Для точек одной и той же ок-
рестности U отождествление множеств p−1( y) вытекает из определения: все они отождествлены с некоторым множеством (U ) . Искомое взаимно однозначное отображение строится как композиция таких отождествлений для подходящей цепочки точек yi нашего пути, лежащих в пересечениях соседних окрестностей, покрываю-
116
щих этот путь. Выбор пути однозначно определяет отождествление точек множеств p−1 ( y1 ) и p−1( y2 ) . Поэтому если задан путь
ϕ: [0, 1] →Y
изадана точка x p−1 (ϕ(0)) , то существует единственный путь
Φ: [0, 1] → X ,
для которого Φ(0) = x и p DΦ = ϕ .
Определение 6.4. Путь Φ называют поднятием пути ϕ. Он однозначно определяется начальной точкой x.
Какие бывают неэквивалентные накрытия над сферой S 2 ?
Определение 6.5. Накрытия |
p1 : X1 → Y и |
p2 : X 2 →Y назы- |
ваются эквивалентными, если |
существует |
гомеоморфизм f : |
X1 → X 2 , что диаграмма |
|
|
X1 →f X 2
2p1 0p2
Y
коммутативна.
§ 25. Расслоения
Понятие накрытия можно обобщить и на случай, когда прообраз точки не является дискретным.
25.1. Локально тривиальное расслоение
Определение 6.6. Локально тривиальным расслоением называется четверка (E, B, F, p) , где E, B, F – топологические простран-
ства, а p : E → B – отображение, обладающее следующими свой-
ствами:
1) у любой точки x B есть окрестность U, полный прообраз которой p−1(U ) гомеоморфен U × F ;
117

2) гомеоморфизм U × F → p−1 (U ) согласован с отображением p, т.е. диаграмма
U × F → p−1 (U )
2 0p
U
коммутативна.
Из условия 2, в частности, следует, что прообраз любой точки гомеоморфен F.
Отображение p называется проекцией, пространство E называется пространством расслоения, пространство B – базой расслоения, пространство F – слоем или типичным слоем расслоения.
Примеры расслоений.
1.Прямое произведение B × F → F . Такие расслоения называются тривиальными.
2.Любое накрытие.
3.Лист Мебиуса – пространст-
|
|
во расслоения над S1 со слоем I. |
|||||
|
|
В самом деле, лист Мебиуса |
|||||
|
|
получается при склейке противо- |
|||||
|
|
положных сторон прямоугольника |
|||||
|
|
(рис. 11). |
|
|
|
||
|
|
Проекция этого расслоения за- |
|||||
Рис. 11 |
|
дается проекцией этого прямо- |
|||||
|
|
угольника на пунктирную сред- |
|||||
|
|
нюю линию. |
|
|
|
||
4. Бутылка Клейна – пространство расслоения над S1 со слоем |
|||||||
S1 . Бутылку Клейна получаем из листа Мебиуса отождествлением |
|||||||
противоположных концов каждого слоя (отрезка). |
|
||||||
5. Расслоение Хопфа: S |
3 |
S1 |
2 |
. Сферу |
S |
3 |
можно предста- |
|
→S |
|
|
||||
вить как множество векторов единичной длины в ^2 . Множество
комплексных прямых в ^2 , проходящих через начало координат, представляет собой одномерное комплексное проективное про-
странство CP1 , гомеоморфное одноточечной компактификации ^ , т.е. гомеоморфное S 2 . Имеется естественное отображение
118
^1 \ {0} → ^P1 ,
сопоставляющее каждому вектору соответствующую комплексную
прямую. |
S 3 , получаем проекцию |
Ограничив это отображение на |
|
S 3 → S 2 . Прообразом каждой точки |
служит пересечение ком- |
плексной прямой с S 3 , т.е. окружность S1 .
Задача 6.1. Доказать, что расслоение Хопфа нетривиально (т.е. оно не сводится к прямому произведению).
Определение 6.7. Расслоения p1 : E1 → B и p2 : E2 → B называются эквивалентными, если существует такой гомеоморфизм
ϕ: E1 → E2 ,
что p1 = p2ϕ .
Определение 6.8. Тривиализацией расслоения p : E → B называется (если существует) гомеоморфизм E → B × F , имеющий вид e → ( p(e), p1 (e)) ,
где p1 (e) F . Для задания тривиализации нужно лишь задать отображение p1 : E → F . Гомеоморфизм тривиализации неединстве-
нен. Более того, две тривиализации могут быть не гомеоморфными.
Пример.
T 2 = S1 ×S1 . |
|
Пусть p-проекция на первый сомножитель S1 . |
Тривилизация |
этого расслоения задается проекцией на второй |
сомножитель |
(рис. 12). Можно взять отображения |
|
(ϕ, ψ) → ψ и (ϕ, ψ) → ψ +ϕ . |
|
Рис. 12
119
Теорема 6.1 (Фельдбау). Любое локально тривиальное расслое-
ние над замкнутым шаром Dk тривиально, т.е. эквивалентно прямому произведению.
(Оставим доказательство этой теоремы читателю.)
Упражнение 6.1. Верно ли, что любое расслоение со слоем Dk тривиально?
Указание 6.1. Рассмотрите лист Мебиуса; при k >1 можно воспользоваться конструкцией расслоенного произведения.
Определение 6.9. Расслоенным произведением локально тривиальных расслоений p : E → B и p′: E′→ B называется расслое-
ние, для которого пространство расслоения состоит из пар (e, e′) , где точки e E , e′ E′ таковы, что p(e) = p′(e′) ; проекция на базу
B определяется очевидным образом. Слоем построенного расслоения является прямое произведение исходных расслоений.
Теорема 6.2 (о накрывающей гомотопии). Пусть p : E → B
локально тривиальное расслоение, ] – клеточное пространство. Пусть заданы отображение
f : ] → E
и гомотопия
F : ]× I → B
отображения
pf : ] → B .
Тогда эту гомотопию можно поднять до гомотопии Φ:
]× I → E отображения f.
25.2.Точная последовательность расслоения
Пусть p : E → B – локально тривиальное расслоение; b0 B –
отмеченная точка; F = p−1 (b ) |
и f |
0 |
F – отмеченная точка. Для |
0 |
|
|
|
пары (E, F ) можно рассматривать относительную гомотопическую |
|||
группу πi (E, F ) . Проекция p : |
E → B индуцирует гомоморфизм |
||
πi (E, F ) → πi (B) ,
посколькуF приэтомотображениипереходитвотмеченнуюточку b0 .
120
