Лебедев-Степанов ВВедение в самосборку ансамблей наночастиц 2012

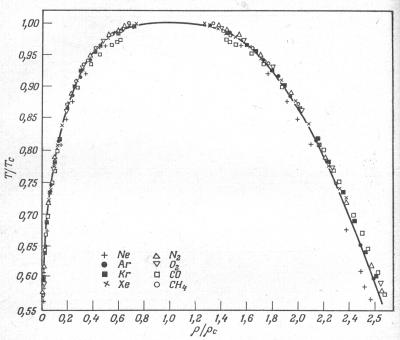
объемов. По крайней мере, такая задача является физически осмысленной.

Рис. 6.1. Сводка данных относительно кривых сосуществования для непроводящих жидкостей [10]

6.2. Дискретный и континуальный подходы

Возможны, условно говоря, два подхода: дискретный и континуальный (на нем основана теория среднего самосогласованного поля, ССП).

Эти подходы следуют из двух представлений функции распределения:

91

В первом случае гамильтониан зависит от координат частиц в фазовом пространстве. Второй случай – гамильтониан определяется локальным значением самой функции распределения.

Функция (6.1) пропорциональна вероятности нахождения частицы в точке фазового пространства с координатами p, q. Гамильтониан частицы, помещенной в эту точку, является мерой этой вероятности. Если гамильтониан может быть представлен в виде

где интегрирование по импульсам может быть проведено независимо от интегрирования по координатам (см. главу 3). При этом остается часть функции распределения, зависящая только от пространственных координат:

Если потенциальная энергия частицы с координатами q определяется парными потенциалами взаимодействия данной частицы со всеми остальными N–1 частицами , то

i=1

При этом полная потенциальная энергия определяется формулой

1 N -1

U = ∑ϕ(q j − qi ) . (6.7)

2 i=1

j ¹i

Нормировка (6.5) осуществляется на полное число частиц

92

Формула (6.7) указывает, что энергия каждой частицы зависит от координат всех остальных частиц, т.е. всего ансамбля. Число частиц велико, поэтому нужно ввести определенные упрощающие предположения, связанные с усреднением положения остальных частиц относительно данной частицы. Разработаны специальные методы расчета усредненного взаимного расположения частиц, позволяющие рассчитывать потенциальную энергию ансамбля. Кроме того, предложены сложные процедуры учета тройных и более высокого порядка столкновений.

Согласно существующим представлениям (отвечающим дискретному подходу, при котором рассматривается функция распределения всего ансамбля частиц в фазовом пространстве, размерность которого есть сумма размерностей пространств, отвечающих степеням свободы составляющих его частиц) наиболее общее статистическое описание процессов в газе может быть получено на основе уравнения Лиувилля — уравнения для функции распределения координат и импульсов всех частиц.

Решение уравнения Лиувилля равносильно решению системы уравнений движения для всех частиц системы, что требует неподъемных вычислительных ресурсов. Однако в этом нет практической необходимости, так как для описания процессов в газе обычно достаточно знать функции распределения переменных одной или двух частиц.

Выражение для функции можно получить из уравнения Лиувилля путем интегрирования по переменным всех частиц, кроме одной. Однако уравнение для функции одной частицы оказывается незамкнутым, поскольку в него входит функция двух частиц. Если аналогичным путем получить уравнение для функции двух частиц, то в него войдет функция распределения переменных трех частиц и т. д. Получается цепочка зацепляющихся уравнений для функций распределения, которая эквивалентна исходному уравнению Лиувилля.

93

Ее называют системой уравнений Боголюбова или ББГКИ (Боголюбова– Борна–Грина –Кирквуда –Ивона ). Вследствие чрезвычайной сложности цепочки уравнений для функций распределения естественно стремление получить приближенные замкнутые уравнения для простейших функций распределения.

Примером такого уравнения и служит кинетическое уравнение Больцмана для газа. Переход от уравнения Лиувилля к существенно более простому кинетическому уравнению означает, естественно, переход к более огрубленному описанию процессов в газах. Это возможно благодаря следующему соотношению размеров:

среднее расстояние между молекулами (п — концентрация атомов), λ — средняя длина свободного пробега.

Вследствие этого можно ввести малые параметры r0 3 n или r0 / λ

и рассматривать ряд последовательных приближений. Первое приближение по малому параметру соответствует учету двойных столкновений, второе — тройных и т. д. Кинетическое уравнение Больцмана для одноатомного газа соответствует первому приближению по малому параметру, т.е. приближению парных столкновений. Этому случаю отвечает идеальный газ.

Было сделано много усилий (ставшие классическими работы Энскога, Боголюбова, Грина, Каданова и др.), чтобы учесть в данном приближении парные взаимодействия, временное запаздывание функций распределения и т.д. Однако рассмотрение плотных газов и жидкостей уже не удовлетворяет условиям (6.9), поэтому необходимо рассмотрение практически всего ряда в разложении по данному параметру, что чрезвычайно усложняет задачу, которая до настоящего времени в рамках данного подхода не решена.

Применяются менее строго обоснованные подходы, позволяющие частично обойти указанные трудности. Расчет термодинамических функций в плотных газах производится либо численными методами (метод молекулярной динамики, метод Монте-Карло), либо

94

путем решения модельных интегральных уравнений для парной корреляционной функции молекул газа (например, уравнение Пер- куса–Йевика ) [31–33]. Как правило, интегральные уравнения для корреляционной функции точно учитывают вклады первых трех членов вириального разложения и приближенно — вклады более сложных взаимодействий.

Гораздо больше фундаментальных успехов достигнуто при рассмотрении свойств вещества вблизи критической точки [31–40]. Дело в том, что здесь возможно введение другого малого параметра, характеризующего близость состояния к критическому. В теории критической точки, являющейся частным случаем теории фазовых переходов второго рода, Ландау постулируется вид уравнения состояния жидкости, в предположении, что свободную энергию F(T,V)

можно разложить в аналитический ряд по степеням v = V −VC и

VC

t = T −TC . Результаты теории таковы: критическая изотерма – куби-

TC

ческая парабола p − pc = v3 , кривая сосуществования жидкости и

газа – квадратичная парабола v2 t . Изохорная теплоемкость имеет скачок при критической температуре, а изобарная теплоемкость и

ся как t-1 при V=Vc.

Орнштейн и Цернике учли флуктуации плотности в рамках тех же основных предположений, что привело к известной функции корреляции плотностей

и позволило объяснить аномальное рассеяние света в критической области (критическая опалесценция).

95

Физически теория околокритических явлений Ландау сводится к приближению среднего самосогласованного поля (ССП), пренебрегающего ближним (флуктуационным) порядком. В рамках теории ССП флуктуации можно учесть лишь как малые поправки, путем добавления в разложение для свободной энергии F (Т, V) члена пропорционального квадрату градиента плотности (приближение Орнштейна – Цернике ).

По мере повышения точности эксперимента становилось ясным, что роль флуктуации не сводится к малым поправкам и указанное приближение ССП неверно, по крайней мере, в достаточно близкой окрестности критической точки. Был обнаружен экспериментально ряд отклонений от теории Ландау. Кривая сосуществования ряда веществ описывается скорее кубическим законом, чем квадратичным; изохорная теплоемкость стремится к бесконечности в критической точке по закону, близкому к логарифмическому. Этот результат сразу вызвал большой интерес, так как к тому времени в двух случаях — точном решении Онзагера для плоской решетки Изинга и эксперименте вблизи λ-перехода в Не4 — была получена логарифмическая расходимость теплоемкости.

Возник вопрос о том, существует ли вообще область применимости приближения ССП в жидкостях? Доказана справедливость теории Ландау в системах с бесконечной размерностью пространства либо с бесконечным радиусом действия сил. В системах конечной размерности d и конечным радиусом взаимодействия r0 область

применимости теории существует при t < 1, если r0 > n −1/ 3 (радиус

взаимодействия превышает среднее расстояние между частицами). Из условия малости флуктуационных поправок (∆CV < CV ~ R) получаем область применимости приближения ССП, определяемую критерием Гинзбурга:

В. Л. Гинзбург предложил следующий критерий: теория самосогласованного поля применима, когда в области размеров порядка радиуса корреляции, флуктуации параметра порядка значительно

96

меньше его среднего значения. Параметры теории выражаются через характеристики данного вещества.

В теории критической точки Ландау предполагается, что кинетические коэффициенты не зависят от близости к критической точке. Это предположение не подтверждается экспериментом, что не удивительно, так как в классическом подходе Ландау не учитываются флуктуации «параметра порядка», которые в действительности определяют поведение кинетических величин по обе стороны от точки перехода.

Учет флуктуаций параметра порядка лежит в основе так называемой масштабной (scaling) теории, которая пытается решить проблемы классической теории. Предполагается, что в области температур t < ( r/ro )6 флуктуации уже не малы и их взаимодействие при r0 < r < rс целиком определяет характер возникающих аномалий. Суть «масштабной гипотезы» состоит в следующем. Флуктуации «параметра порядка» (плотности в случае жидкости) вблизи крити-

значений плотности. Радиус корреляции — характерный масштаб в системе — значительно превосходит радиус действия межмолекулярных сил. Можно сказать, что околокритическое состояние — это «газ» капель, размер которых растет по мере приближения к критической точке. В связи с тем, что в критической области флуктуации охватывают области, содержащие большое число частиц, а свойства вещества в данном температурном диапазоне определяются именно флуктуациями, детали межчастичного взаимодействия становятся малосущественными – наблюдается подобие в критическом поведении таких систем. Это подобие получило название принципа универсальности критических явлений, который является обобщением закона соответственных состояний. Индивидуальные свойства жидкостей в рамках масштабной теории пытаются рассматривать как поправки к универсальному нулевому приближению – критическому состоянию.

97

Однако, несмотря на определенные успехи масштабной теории в области критической точки, данная теория всё же является полуфеноменологической и не распространима широко за пределы критической области, несмотря на попытки такого рода. Последовательный учет потенциалов межчастичного взаимодействия в ней также невозможен. Однако нет сомнения, что существование физически осмысленного уравнения состояния, захватывающего критическую область, соответствует действительности. При этом уравнение состояния есть результат усреднения межмолекулярных сил, аналогичный теории ССП.

Это означает, что сама теория ССП должна быть сформулирована таким образом, чтобы, с одной стороны, учесть опыт описания метастабильного состояния масштабной теорией (и приводить в данной области к тем же приближениям), а с другой – опираться на статистические методы, где используется ССП, которые, в свою очередь, необходимо перенести на области, в где критерий Гинзбурга не выполняется, т.е. флуктуации плотности велики, превышая среднее расстояние между молекулами.

Но это фактически означает необходимость развития нового представления о среднем поле, при котором описание взаимодействия большого количества атомов через среднюю по времени концентрацию и ее связанные с температурой флуктуации является фундаментальным положением теории.

При адекватной формулировке континуальный подход имеет самостоятельное фундаментальное значение и может рассматриваться как альтернативный фундаментальный способ задания коллективных потенциалов межчастичных взаимодействий при условии, что понятие средней концентрации (или средней плотности вещества) хорошо определено. Хорошая определенность в свою очередь предполагает учет связанных с температурой флуктуаций концентрации при усреднении по времени взаимного расположения молекул, что необходимо для определения средней (по времени) потенциальной энергии ансамбля частиц.

Потенциальная энергия зависит как от средней концентрации частиц, так и температуры, которая определяет масштаб флуктуаций

98

плотности в окрестности каждой частицы. Кинетическая энергия также может быть сформулирована как функция градиентов плотности флуктуационной природы при использовании кинетических коэффициентов.

Поэтому вместо парных, тройных и т.д. потенциалов в качестве исходного допущения можно использовать некоторые обоснованные из общих позиций выражения зависимости плотности потенциальной энергии от средней концентрации. Энтропийные эффекты в данной модели учитываются через флуктуации концентрации. В этом случае исходная функция распределения в конфигурационном пространстве (концентрация) имеет вид

где δn(nq (q),T ) – флуктуационная часть плотности. (Данный вид выражения носит во многом символический характер.)

6.3. Парные потенциалы

Между дискретным и континуальным описанием энергии существует переход. При использовании парных потенциалов нужно знать функциональную форму этих потенциалов и парную корреляционную функцию (табл. 6.1).

Таблица 6.1

99

Потенциал типа прямоугольной ямы

U = ∞ , r < σ

U = −ε , σ £ r £ gσ

U = 0 , r > σ

Потенциал Сазерленда

100