
Алексеев Нейтронные методы в физике конденсированного состояния 2012
.pdf
ке. В этом смысле его происхождение аналогично происхождению рентгеновского формфактора, хотя аналогия неполная, из-за наличия спиновой составляющей взаимодействия. Размер электронной оболочки непосредственно определяет зависимость формфактора от переданного импульса. Точечное распределение соответствует формактору, не зависящему от Q, очень протяженное распределение – резко изменяющемуся формфактору, т.е. рассеянию, сконцентрированному в области малых углов, либо больших длин волн (малых Q).
На рис. 13.1 нейтронный магнитный формактор сравнивается с рентгеновским.
Рис. 13.1. Сопоставление характера зависимости от импульса для формфакторов d-элемента (марганец), приведенных по амплитуде. Тонкая линия – рентгеновский, жирная – нейтронный. Для f-элементов (пунктирная линия) нейтронный формфактор более пологий из-за более высокой степени локализации f-электронной оболочки
121

Для гамма-лучей имеется систематическая зависимость амплитуды рассеяния от атомного номера, т.е. числа электронов в атоме (с учетом валентного состояния), а характер q-зависимости для самого формфактора изменяется слабо. Для нейтронов – характер q- зависимости формфактора в основном связан с типом (d-, f-) электронной оболочки и в большинстве случаев (но не всегда!) не сильно зависит от числа этих электронов, а сама амплитуда рассеяния определяется магнитным моментом.
Атомные орбитали (f-, d-), определяющие магнитные свойства атома, имеют сложную форму, их свойства определяются в том числе и релятивистскими эффектами, поэтому в основе вычисления магнитных формфакторов сложные формулы. В большинстве обычных случаев достаточно дипольного приближения, т. е. элек-
тронные оболочки рассматриваются как сферические. Это справед-
ливо, когда Q-1 >>re, (re ~3 10-2 Å), т.е. Q <100 Å-1.
Формфактор удобно представить как линейную комбинацию функций, описывающих радиальное распределение орбитальной и спиновой плотности, <j2> и <j0>, соответственно (фактически это интегралы от произведения соответствующего радиального распределения электронной плотности на функции Бесселя 0-го и 2-го порядка):
F (Q) = j0 (Q) + |
2 − g |
j2 (Q) . |
(13.5) |
|
g |
||||
|
|
|
Для 3d-металлов орбитальный вклад отсутствует (из-за кристаллического электрического поля (КЭП) которое, действуя на орбитальный момент и преодолевая спин-орбитальную связь, выводит его из «игры» из-за сильного снятия вырождения по орбитальному квантовому числу – так называемого эффекта «замораживания» орбитального момента), и все определяется (<j0>)2 , т.е. членом разложения, связанным со спиновым моментом.
Для РЗ элементов ситуация меняется – орбитальный вклад соизмерим со спиновым (спин-орбитальное взаимодействие сильнее взаимодействия с КЭП).
На рис. 13.2 и 13.3 показаны примеры формакторов для d- и f- элементов.
Видно, что формфактор для d-элементов более крутой, что связано с большей, по сравнению с f-электронами, степенью делокали-
122

зации радиальной части волновой функции электронов d-оболочки, и отсутствием вклада от орбитальной части.
Рис. 13.2. Зависимость квадрата формфактора (в данном случае - <j0>2 , см. текст) и его составляющих – спиновой <j0> иорбитальной <j2> от переданного импульса для иона меди
В случае f-элементов магнитный формфактор может отличаться от «колоколообразной» кривой, демонстрируя немонотонное поведение (Sm3+) из-за комбинированного действия орбитальной и спиновой составляющих. Хотя (как видно из рис. 13.3), если отсутствует аномально высокий весовой фактор орбитального вклада, то суммарные формфакторы для разных элементов отличаются слабо, что иллюстрирует пример Nd - и Yb – элементов начала и конца редкоземельного ряда. Следует подчеркнуть, что в общем случае формфактор определяется характером магнитного рассеяния (упругое на вырожденном мультиплете, неупругое на состояниях мультиплета, когда вырождение снято, межмультиплетное, и т. д.), и для возбуждений он может отличаться (и сильно!) от формфакторов, приведенных на рис. 13.3.
123
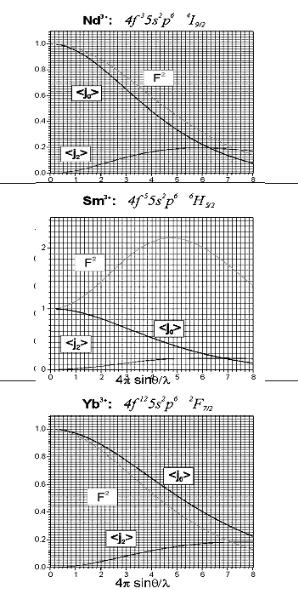
Рис. 13.3. Зависимость квадрата формфактора(F2) и его составляющих<j0> и <j2> от переданного импульса для ионов редкоземельных элементов (Nd3+, Sm3+, Yb3+), отличающихся числом f-электронов
124

Здесь они соответствуют рассеянию без передачи энергии, поэтому вместо Q ось абсцисс обозначена через длину волны и угол рассеяния – подход характерный для дифракционных представлений. Анализ всех возможных вариантов для Q-зависимостей формфактора выходит за пределы настоящего курса, хотя и весьма интересен с точки зрения понимания характера информации, которая может быть получена из нейтронного эксперимента.
13.2. Возбуждения в магнитоупорядоченных средах
Магнитное когерентное рассеяние нейтронов на магнитоупорядоченном (TN=122 K) кристалле MnO было впервые продемонстрировано Клиффордом Шаллом в 1949 г. Его классический эксперимент (нейтронная дифрактограмма показана на рис. 13.4) доказал существование антиферромагнетизма.
Рис. 13.4. Экспериментальные нейтронограммы К. Шалла для окиси марганца, измеренные выше и ниже температуры антиферромагнитного упорядочения TN=122 К. Пик, обусловленный магнитным рассеянием появляется ниже TN на месте запрещенного кристаллической симметрией рефлекса (111)
125

Четко виден пик при угле рассеяния порядка 6о, который появляется ниже температуры Нееля и соответствует удвоенному периоду кристаллической решетки (111)mag на рисунке. Ранее антиферромагнетизм был лишь умозрительной моделью, разработанной Л. Неелем и Л.Д. Ландау.
Магнитные моменты в кристаллических веществах могут упорядочиваться ферромагнитным (FM), антиферромагнитным (AF), ферримагнитным, геликоидальным, спиральным образом. Все эти магнитные структуры дальнего порядка хорошо идентифицируются методом нейтронной дифракции.
При помощи этого метода можно устанавливать сложные магнитные фазовые диаграммы материалов, рис. 13.5 показана фазовая диаграмма NdCu2, полученная нейтронографическим методом.
μ H (T) 0
4 |
|
|
|
|
|
|
FM |
|
|
F2 |
|
|
|
|
2 |
|
|
|
|
F1 |
|
|
|
|
AF1 |
|
AF2 |
AF3 |
|
00 |
2 |
4 |
6 |
8 |
T (K)
Рис. 13.5. Фазовая диаграмма в координатах магнитное поле – температура, экспериментально определенная с помощью нейтронной дифракции для
NdCu2
При помощи неупругого магнитного рассеяния нейтронов можно исследовать магнитные возбуждения – спиновые волны (магноны при квантово-механическом описании).
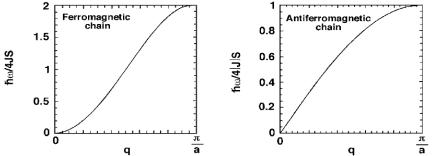
Законы дисперсии ферромагнитной и антиферромагнитной спиновых цепочек показаны на рис.13.6.
Ферро- и антиферромагнетики различаются характером дисперсии при малых волновых векторах, которая описывается квадратичной и линейной зависимостью, соответственно.
126
a) |
b) |
Рис. 13.6 Законы дисперсии спиновых волн в ферро- (а) и антиферромагнитной (б) одномерной цепочке с взаимодействием ближайших соседей. Энергия нормирована на обменное взаимодействие ближайших соседей
Сечение магнитного рассеяния на магнонах задается выражени-
ем:
|
|
d 2 |
σ |
|
|
± |
γe2 |
2 |
1 |
|
2 k f |
|
2 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gF (Q) |
|
|
|
+ Qz ) |
|
S |
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
2 |
|
exp[− 2W (Q)](1 |
2 |
|||||||||
dΩdE |
mc |
|
|
|
|
k0 |
|
|
|
|||||||||||||||
|
|
2π3 |
∑ |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
× |
|
|
|
nq + |
|
|
|
± |
|
|
|
δ(hωm hω)δ(Q m q − τ), |
|
(13.6) |
||||||||||
|
v0 |
|
2 |
|
2 |
|
|
|||||||||||||||||
|
|
|
|
q,τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
которое сходно с выражением для когерентного рассеяния на фононах, но интенсивность здесь определяется формфактором, величиной спина (в общем случае – магнитного момента), а также величиной, зависящей от взаимной ориентации спина и переданного импульса (см. раздел 4). Если, например, Q = Qz, то в рассеянии участвуют δSx и δSу компоненты спиновой переменной, если Qz=0, то интенсивность вдвое меньше, так как в рассеянии эффективно участвует только одна из двух компонент (x, y) флуктуации спина.
Ясно, что при числе магнитных атомов в примитивной ячейке больше одного возникают дополнительные ветви возбуждений, по аналогии с фононными оптическими ветвями. Пример экспериментального исследования магнонов в системе с двумя магнитными атомами в примитивной ячейке показан на рис. 13.7.
127
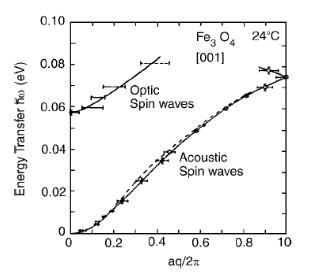
Рис. 13.7. Структура спектра магнитных возбуждений для ферромагнитного соединения Fe3O4 с двумя магнитными атомами в примитивной ячейке структуры
Очень мощным (но и более сложным, в силу ряда причин методического характера) экспериментальным методом является рассеяние поляризованных нейтронов, которое может быть с анализом конечной поляризации или без него, в зависимости от характера решаемых задач.
13.3.Физические задачи, решаемые
спомощью поляризованных нейтронов
При наличии выделенного направления (внешнего поля) нейтроны приобретают ориентацию спинов: по- и против его направления: n+ и n- Тем или иным способом можно изменить соотношение этих двух поляризаций в пучке нейтронов – тем самым создать пучок поляризованных нейтронов с преобладанием одного направления спинов.
Важной характеристикой пучка поляризованных нейтронов является:
P=(n+-n-)/(n++n-) – степень поляризованности.
128

Реально достижима поляризованность до 0.99. В экспериментах имеет смысл работать с пучком, где Р не меньше 0.85. Поляризация нейтронных пучков осуществляется при помощи поляризаторов (рис. 13.8) различного принципа действия и технического устройства.
Рис. 13.8. Поляризатор за счет тех или иных физических явлений обеспечивает сохранение в прошедшем или отраженном пучке одной из двух поляризаций во внешнем («ведущем») поле BG
В качестве поляризаторов используются:
-поляризационные фильтры (3He в магнитном поле);
-отражение от ферромагнитных кристаллов (Heusler alloy);
-отражение от поляризующих суперзеркал.
Типичная схема эксперимента на поляризованных пучках показана на рис. 13.9. Флипперы позволяют переворачивать спин по отношению к первоначальному направлению, т.е. инвертировать исходную поляризацию пучка. Таким образом, если на образец падает полностью поляризованный пучок, а после прохождения через образец часть спинов изменила свою ориентацию на противоположную в результате взаимодействия с компонентой магнитного момента, перпендикулярной к поляризации (см. раздел 4) пучка, то включая флиппер 2 мы можем выделить в спектре рассеянных нейтронов вклад от этой части, а выключив его – от части, соответствующей рассеянию без переворота спина.
129

Рис. 13.9 Схема эксперимента с возможностью выделения четырех типов взаимодействия (в кружках) в зависимости от взаимной ориентации спинов до и после рассеяния на образце и по отношению к магнитному, полю (вертикальному – показано жирной стрелкой), приложенному к образцу
На рис. 13.10 показан пример разделения вкладов от магнитного
(в основном, spin-flip SF) и немагнитного (non spin-flip NSF) рассея-
ния в спектроскопическом эксперименте на поляризованных нейтронах.
a) |
b) |
Рис. 13.10. Спектры (на границе зоны Бриллюэна – a) , в центре зоны – b)) рассеяния нейтронов на монокристалле YbB12 с f-электронным (магнитным) и фононным вкладом в рассеяние в одной области энергий. Кружки – рассеяние с переворотом спина (SF, - магнитная составляющая ), точки – без переворота (NSF - ядерная составляющая). Температура образца 5 К
130
