
Семинары Алексеевой
.pdf
Частный случай двухосного НС – чистый сдвиг ( 2 0 |
, 1 3 |
|||||
|
|
|
50 МПа |
|
||
|
1 |
|
|
|
|
|
|
50 |
|
|
2 |
0 |
|
|
|
|
|
|
||
50 |
3 |
50 МПа |
|
|||
)
Одноосное (линейное) НС – одноосное растяжение
 50
50
1 50 МПа
2 0 |
, |
3 0 |
Одноосное (линейное) НС – одноосное сжатие
50
1 0 , 2 0 ,3 50 МПа

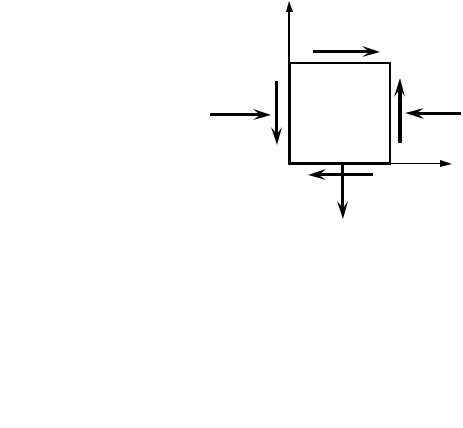
2) Случай, когда одно из главных напряжений известно
y |
|
|
z |
|
z
 y
y
|
xy |
|
yx |
|
|
||
|
|
|
|
|
|
x |
|
|
|
x |
|
Главные напряжения
|
|
|
|
|
|
гл |
|
z |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
σ |
|
σ |
|
|
|
|
σ |
|
σ |
|
|
2 |
|
σгл |
x |
y |
|
x |
y |
2 |
||||||||
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
2 |
|
τxy |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Формула для определения положения главных площадок
tg2 |
2 xy |
|
|
. |
|
x y |
||
x и y - нормальные напряжения в неглавных площадках
Если известное главное напряжение будет иметь другой индекс, то
следует изменить индексы у нормальных и касательных напряжений!
Пример 1. |
гл ? направления |
гл ? |
||||||
|
|
|
200 |
250 |
0 |
|
|
|
|
T |
|
|
250 |
300 |
0 |
|
, МПа |
|
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|||
y
 300
300
250 200
x
x
200
МПа
,
y
300 |
||
|
гл |
|
|
|
|
МПа , |
||
|
z |
0. |
|
|
|
xy
yx
250
МПа
.
гл |
200 300 |
|
200 300 2 |
250 |
2 |
50 |
354 МПа , |
||
2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||
|
50 354 404 МПа, |
|
|
|
|
|
|||
гл |
гл 50 354 304 МПа. |
||||||||

Присваиваем индексы
1
404 МПа
;
2
0
;
3
304 МПа
.
tg2
2 250 |
1, |
2 45 |
, |
22,5 . |
||
200 300 |
||||||
|
|
|
|
|
||
|
y |
22.5 |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
||
304 |
|
404 |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
x |
|
|
|
|
|
|
22.5 |
|
304  3
3
404

Пример 2. |
гл ? |
направления гл ? |
||||||
|
|
|
0 |
0 |
30 |
|
|
|
T |
|
|
0 |
120 |
0 |
|
, МПа |
|
|
|
|||||||
|
|
|
|
|
|
|||
|
|
|
30 |
0 |
80 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
y 120 МПа, z |
80 МПа, |
|||||||
|
zx xz 30 МПа. |
|
|
|||||
z
y
80
 120
120
30
 x
x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гл |
|
y |
120 МПа. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 80 |
|
|
0 ( 80) |
|
2 |
|
|
|
|
||
|
|
|
x |
z |
|
x |
z |
|
2 |
|
|
|
30 |
2 |
40 |
50 МПа. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
гл |
|
|
2 |
|
|
|
2 |
|
xz |
|
2 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 МПа. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
гл 10 МПа, |
гл |
|
|
|
|
|||||||||||

Присвоим индексы:
1 10 МПа , |
2 90 МПа ; |
||
|
3 |
120 МПа. |
|
|
|
|
|
Положение главных площадок
tg2 |
|
2 |
xz |
|
|
2 30 |
0,75; |
|
|
|
|
|
|
||||
|
|
|
0 ( 80) |
|||||
|
x |
z |
|
|||||
|
|
|
|
|
|
|
||
|
2 36,8 |
; |
18,4 . |
|||||
2  90
90
10
z
10
 90
90
18,
1 4
x

3) Случай, когда все площадки неглавные
Решается кубическое уравнение
σ3гл I1 σгл2 I2 σгл I3 0,
где
I1 x y z , |
|
|
|
|
|
|
|
||||||||
I |
2 |
|
|
y |
|
|
z |
|
|
x |
2 |
2 |
2 |
, |
|
|
x |
|
|
y |
|
z |
|
xy |
yz |
xz |
|
||||
|
|
σx |
|
τ yx |
τzx |
|
|
|
|
|
|
|
|||
I3 |
τxy |
σ y |
τzy . |
|
|
|
|
|
|
||||||
τxz τ yz σz

Пример 3. |
гл ? |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
0 |
|
40 |
|
|
|
|
|
|
|
|
T |
|
|
0 |
0 |
|
30 |
|
, МПа |
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
40 |
30 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
yz |
|
zy |
30 МПа, |
|
zx |
|
xz |
40 МПа. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
y
30
40
z
 x
x
Ни одна из площадок не является главной!
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
40 |
|
I 0, |
I |
|
30 |
2 |
40 |
2 |
2500 MПа |
2 |
, |
I |
|
|
0 |
0 |
30 |
0. |
|
2 |
|
|
|
3 |
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
30 |
0 |
|
Кубическое уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σ3гл 2500 σгл 0, |
|
|
|
σгл σгл 50 σгл 50 0, |
|
|
|
|
|||||||||
1 50 МПа , |
2 0 , |
3 50 МПа |
|
|
|
|
|
|
|
|
|
||||||
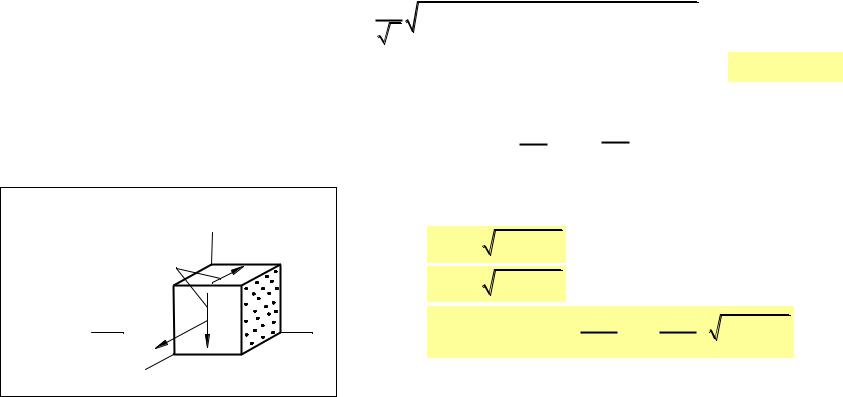
Теории прочности
1. Теория прочности максимальных касательных напряжений (Треска-Сен-Венана)
|
|
|
|
|
|
экв |
|
|
3 |
|
1 |
|
2. Теория прочности энергии формоизменения (Хубера-Мизеса)
σ |
|
|
1 |
(σ σ |
|
) |
2 |
(σ |
|
σ |
|
) |
2 |
(σ |
|
σ ) |
2 |
|
|
|
|
|
|
||||||||||||
экв |
|
2 |
|
2 |
3 |
|
3 |
|
|||||||||
|
i |
2 |
1 |
|
|
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 и 2 применимы только для пластичных материалов, у которых
3. Теория Мора
|
|
|
σ |
вр |
|
|
|
σ |
тр |
|
|
σэкв σ1 k σ3 |
, |
k |
, |
|
k |
, |
. |
||||
|
|
||||||||||
|
|
|
|||||||||
|
|
|
|
||||||||
σ |
|
|
σ |
|
|||||||
|
|
|
вс |
|
|
|
тс |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
тр |
σ |
тс |
|
|
σт
.
точка А y
|
|
Упрощенное плоское напряженное состояние (УПНС) |
||||||||||
|
|
точка B |
|
|
|
|
|
|
|
|
|
|
|
|
y |
1. |
σэкв |
σ |
2 |
4τ |
2 |
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
σэкв |
σ |
2 |
3τ |
2 |
|
|
||
|
|
|
|
|
|
|
||||||
x |
|
x |
3. |
|
экв |
k |
3 |
1 k |
1 k 2 4 2 |
|||
|
|
|
|
|
|
1 |
|
|
2 |
2 |
||
|
|
|
|
|
|
|
|
|
|
|
||
z

3. Исследование НС в различных точках нагруженного тела
Пример 4.
120
50 
Дано: тр тс т |
(пластичный материал) |
Определить экв ? |
|
120 |
МПа |
1 |
|
2 50 МПа
|
3 |
0 |
|
|
Теория I (Треска-Сен-Венана):
|
экв |
|
|
3 |
|
1 |
|
Теория II (Хубера-Мизеса):
120 0 120
МПа
,
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
σ |
экв |
|
|
|
(σ |
σ |
2 |
)2 |
(σ |
2 |
σ |
3 |
)2 |
(σ |
3 |
σ )2 |
|
|
702 502 1202 |
104,7 МПа. |
|||||
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теория I дает завышенные значения экв . Теория II – заниженные. Истинное – между ними.
