5.3 Сведения из теории

В усилительных каскадах радиоприемников широко используются избирательные цепи, состоящие из параллельно соединенных катушки индуктивности и конденсатора, называемые простым колебательным контуром. Цепи с двумя катушками индуктивности или с двумя конденсаторами, включёнными в разных ветвях, называются сложными контурами.

Три варианта схем параллельного колебательного контура изображены на рисунке 5.4.

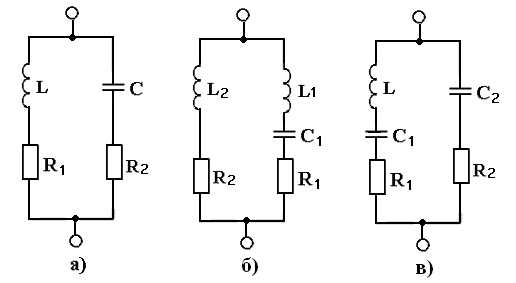
Рисунок 5.4 – Три варианта схем параллельного колебательного контура

Схема, обобщающая три разновидности параллельного контура, показана на рисунке 5.5.

Рисунок 5.5 – Обобщенная схема параллельного контура

Зависимость комплексного сопротивленияпараллельного контура (рисунок 5.5) от частоты питающего его гармонического источника тока определяется выражением:

(5.1)

где ,– сопротивления потерь, характеризующие потери в катушке индуктивности и конденсаторе.

Сопротивление потерь ив реальной схеме, как детали (резисторы), отсутствуют.

В простом колебательном контуре обычно величиной пренебрегают (<<) и, принимая=, его комплексную проводимостьможно записать в виде:

;

Реактивная проводимость Вопределяется выражением:

.

Режим работы параллельного колебательного контура, при котором его реактивная проводимость (реактивное сопротивление) равна нулю, называется резонансом токов.

Условие резонанса токов имеет вид:

. (5.2)

Резонансная частота контура определяется выражением:

. (5.3)

На резонансной частоте сопротивление катушки индуктивности и конденсатора равны по величине и противоположны по знаку. Модуль этих сопротивлений называется характеристическим сопротивлением контура

. (5.4)

Отношение характеристического сопротивления к сопротивлениюRназывается добротностью контураQ:

. (5.5)

При резонансе ток контура превосходит ток неразветвленной части цепи в Qраз, поэтому явление резонанса в параллельном контуре и называют резонансом токов.

Комплексное сопротивление параллельного колебательного контура определяется выражением:

(5.6)

где – обобщенная расстройка.

На резонансной частоте сопротивление контура активно, максимально и равно:

. (5.7)

Модуль выражения (5.6)

(5.8)

называют амплитудно-частотной характеристикой контура, а аргумент этого выражения – фазо-частотной характеристикой контура. Эти характеристики изображены на рисунке 5.6.

Рисунок 5.6 – Амплитудно-частотная и фазо-частотная

характеристики простого контура

Полосой пропускания контура называют область частот, на границах которой сопротивление контура меньше резонансного значениявраз. На границах полосы пропускания=1.

Полосы пропускания параллельного контура можно определить по формуле:

. (5.9)

Если источник сигнала с внутренним сопротивлением R_i представить в виде эквивалентного генератора тока (рисунок 5.7), то эквивалентное сопротивление этой схемы будет равно параллельному соединению сопротивленийR_i и:

. (5.10)

Рисунок 5.7 – Схема параллельного контура с учетом

внутреннего сопротивления генератора

Добротность эквивалентного контура будет определяться выражением:

. (5.11)

На рисунке 5.8 приведено несколько зависимостей от частоты источника тока при различных значенияхR_i.

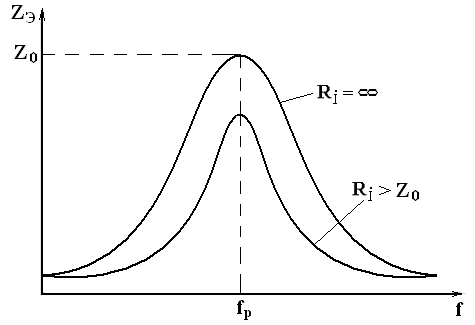
Рисунок 5.8 – Зависимость эквивалентного сопротивления от частоты

при различных значениях R_i

Из рассмотрения рисунка 5.8 видно, что с уменьшением R_iуменьшается резонансное сопротивлениеи добротностьи увеличивается полоса пропускания

. (5.12)

Физический смысл уменьшения добротности заключается в том, что доля энергии, переходящая в тепло, увеличивается за счет нагревания сопротивления R_i.

Применение параллельного колебательного контура целесообразно с точки зрения только в том случае, когда внутреннее сопротивление генератора достаточно велико (R_i>>Z₀). Однако следует учесть, что с увеличением внутреннего сопротивления генератора сама величина напряжения на контуреU_Кпадает, так как

(5.13)

В отличие от простого параллельного колебательного контура сложный параллельный колебательный контур с неполным включением емкости (рисунок 5.3) характеризуется еще одним параметром – коэффициентом включения p_c, равным:

. (5.14)

Поскольку такой контур содержит в качестве одной из ветвей последовательный колебательный контур, в нем наблюдается как резонанс токов, так и резонанс напряжений. Частота резонанса рассчитывается по формуле:

, (5.15)

где .

Частота резонанса напряжения определяется параметрами последовательного колебательного контура:

. (5.16)

Поскольку <, частота резонанса напряженийбудет всегда меньше частоты резонанса токов. Данное обстоятельство является признаком контура с неполным включением емкости. Характеристическое сопротивлениеи добротностьна частоте резонанса токов определяется выражением:

, (5.17)

. (5.18)

Сопротивление контура на частотеносит активный характер, максимально и определяется выражением:

. (5.19)

Напряжение на контуре на этой частоте также будет достигать максимального значения.

Сопротивление контура на частотеносит активный харак-тер, минимально и практически равноR:

. (5.20)

Напряжение на этой частоте также будет минимальным.

Амплитудно-частотная характеристика контура с неполным включением емкости изображена на рисунке 5.9.

Рисунок 5.9 – Амплитудно-частотная характеристика контура

с неполным включением емкости

Фазо-частотная характеристика этого же контура приведена на рисунке 5.10.

Рисунок 5.10 – Фазо-частотная характеристика контура

с неполным включением емкости

Если ко входу контура подключается источник напряжения с внутренним сопротивлением , то эквивалентная добротность контурападает, а полоса пропусканияувеличивается, их величины рассчитываются по формулам (5.11) и (5.12) соответственно.