Сферична астрономія

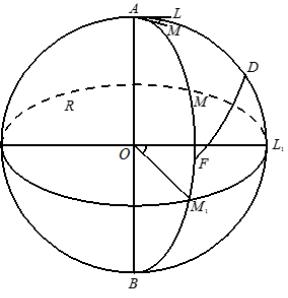
Рис. 1.2. Сферичний кут

Сферичні кути виражаються в градусній мірі і вимірюються плоским лінійним кутом між дотичними, проведеними до його сторін з вершини сферичного кута. На рис. 1.2 це кут LAM, що дорівнює центральному кутові L1ОM1 і дорівнює дузі L1M1. Значить, мірою сферичного кута служить дуга великого кола L1M1, укладена між продовженням сторін кута і яка має полюс у вершині сферичного кута. Ця дуга віддалена від вершини сферичного кута на 90°. Наведена на рис. 1.2 дуга великого кола DF не дорівнює сферичному куту DAF і не є його мірою. У даному випадку не виконуються умови щодо дуги

L1M1.

1.2. Сферичний трикутник, його властивості

Сферичним трикутником називається криволінійний трикутник на поверхні сфери, утворений перетином трьох дуг великих кіл. Елементами сферичного трикутника є сферичні кути і сторони, які зазвичай виражаються в градусній мірі. Кути сферичного трикутника прийнято позначати великими літерами латинського алфавіту, а сторони - малими буквами відповідно найменуваннями протилежних вершин. На рис. 1.3 зображено сферичний трикутник АВС, кути якого позначені літерами А, В, С, а сторони – a, b, c.

Неважко побачити, що кожному сферичному трикутнику АВС відповідає тригранний кут ОАВС при центрі сфери, отримуваний перетином площин трьох великих кіл, дуги яких утворили сторони трикутника. Кожен плоский кут тригранного кута відповідає стороні сферичного трикутника: CОB = a;

AОC = b; AОB = c.

11

Рис. 1.3. Сферичний трикутник

Кожен двогранний кут у тригранному куті є рівним відповідному куту сферичного трикутника, оскільки будь-який двогранний кут вимірюється лінійним кутом між перпендикулярами, установленими з довільної точки ребра в площинах його граней. Так, А = 1, В = 2, С = 3 (див. рис. 1.3).

Враховуючи, що всі властивості плоских і двогранних кутів тригранного кута повністю поширюються на елементи сферичного трикутника, можна зробити наступні висновки.

1.Проти рівних сторін у сферичному трикутнику лежать рівні кути: проти більшої сторони лежить більший кут, і навпаки.

2.Сума двох будь-яких сторін у трикутнику завжди є більшою, а різниця їх завжди меншою третьої сторони.

3.Якщо різниця двох сторін більша, дорівнює або менша нуля, то й різниця двох протилежних їм кутів більша, дорівнює або менша нуля.

4.Сума всіх сторін будь-якого сферичного трикутника не перебільшує

360°.

5.Сума всіх кутів будь-якого сферичного трикутника завжди більша 180°, але менша 540°. Різниця між сумою кутів у сферичному трикутнику і 180° називається сферичним надлишком і позначається :

Сферичний надлишок завжди додатний і менший 360°.

6.Сума двох кутів сферичного трикутника за вирахуванням третього завжди менша 180°.

7.Якщо сума двох кутів в трикутнику більша, дорівнює або менша 180°, то й сума двох протилежних їм сторін повинна бути більшою, дорівнювати або меншою ніж 180°.

12

У процесі розв’язку сферичних трикутників треба стежити, щоб значення елементів трикутника задовольняли переліченим правилам. Слід також остерігатися помилкового висновку про те, що будь-який кут сферичного трикутника дорівнює протилежній стороні. Це справедливо лише у тому випадку, коли вершина цього кута є полюсом протилежної сторони, тобто, коли обидві інші сторони рівні 90°.

Сферичні трикутники, розташовані на одній сфері, рівні між собою, якщо три будь-яких елементи одного трикутника відповідно рівні трьом елементам іншого і вони розташовані в трикутниках однаковим чином. Якщо ж три елементи одного сферичного трикутника відповідно рівні трьом елементам іншого, але розташовані в обох трикутниках неоднаково, то такі трикутники є симетричними один одному. Очевидно, що симетричні трикутники рівновеликі, тобто займають однакові за площею поверхні сфери.

Залежно від значень кутів та сторін сферичні трикутники розділяють на косокутні, прямокутні і четвертні (прямосторонні). У загальному випадку сферичні трикутники є косокутними. Сферичний трикутник, один з кутів якого дорівнює 90°, називають прямокутним. У прямокутному сферичному трикутнику сторони, що утворюють прямий кут, називають катетами, а сторону, що лежить проти прямого кута – гіпотенузою. Якщо в сферичному трикутнику одна зі сторін дорівнює 90°, його називають четвертним. Рівними 90° можуть бути дві і навіть три сторони трикутника.

При розгляді деяких питань геодезичної астрономії доводиться мати справу з вузькими і елементарними трикутниками. Вузькі сферичні трикутники мають одну досить малу у порівнянні з двома іншими сторонами сторону. Кут, протилежний малій стороні, теж є дуже малим. Що ж слід розуміти під поняттями «мала сторона» або «малий кут»? При допустимій похибці вимірів 1" ці значення не повинні перевищувати 1,5°. На підставі загальної властивості сферичних трикутників, що b – c < a, різниця великих сторін вузьких трикутників теж мала. При розв’язку вузького сферичного трикутника тригонометричні функції елементарно малих величин (сторони і кута) зазвичай заміняють першими членами розкладів у ряд:

(1.5)

Елементарним сферичним трикутником називають трикутник, у якого всі три сторони досить малі. Такі сферичні трикутники практично з достатньою точністю можна розв’язувати як плоскі, використовуючи формули прямолінійної тригонометрії. Якщо відомо, що у сферичному трикутнику дві сторони є досить малими, то це елементарний трикутник, бо за загальною властивістю сферичних трикутників a < b + c.

13

Надалі будемо розглядати на сфері лише так звані Ейлерові трикутники, тобто такі трикутники, всі сторони і кути яких менші ніж 180°.

1.3. Основні формули сферичної геометрії. Мнемонічне правило Непера-Модюі

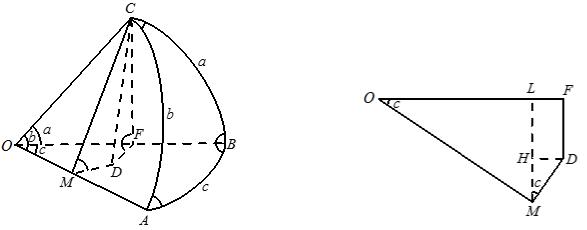
Установимо основні залежності між елементами в косокутному сферичному трикутнику. Для цього розглянемо трикутник АВС (рис.1.4), розташований на поверхні сфери одиничного радіуса з центром у точці О.

Проведемо через вершину С площину, перпендикулярну до радіусу ОА, та іншу площину, перпендикулярну до радіуса ОВ. Перша площина перетинає площину СОА по лінії СМ, а площину АОВ – по лінії МD. Друга площина перетинає площину СОВ по лінії СF, а площину АОВ – по лінії FD. Кожна з названих площин перпендикулярна до площини АОВ, а значить перпендикулярна до неї і лінія їх перетину CD. Отже, кути CMО, DMО, CFО і DFО – прямі кути. Кут CMD дорівнює сферичному куту A, а кут CFD – сферичному куту B; кути BОC, CОA і BОA відповідно рівні сторонам a, b і c трикутника ABC.

З прямокутного трикутника CОM, оскільки радіус сфери дорівнює одиниці, маємо:

Рис. 1.4. До виведення формул сферичної Рис. 1.5. Чотирикутник ОFDM в плані

14

геометрії

На рис. 1.5 фігура ОFDM показана в плані на площині ВОА. В утвореному чотирикутнику ОFDM проведемо лінію ML паралельно лінії DF і лінію DH паралельно лінії ОF. Утворились прямокутні трикутники ОLM і DHM. Кут DMH дорівнює кутові MОL, оскільки це кути з перпендикулярними сторонами. Оскільки кут MОL дорівнює кутові с, то і кут DMH також дорівнює кутові c. Очевидно, що:

(1.12)

(1.13)

Одна з формул для розв’язання сферичного трикутника називається

формула косинуса сторони та має формулювання: у всякому сферичному трикутнику косинус будь-якої сторони дорівнює добутку косинусів двох інших сторін плюс добуток синусів тих же сторін на косинус кута між ними

Ця формула пов'язує між собою три сторони і один з кутів сферичного трикутника.

Доведення. Замінюючи в рівнянні (1.12) літерні позначення рівняннями (1.6), (1.8) і (1.9), отримаємо рівняння (1.14), що й необхідно було довести. Аналогічно доводяться і записуються формули для інших сторін трикутника.

Для розв’язання сферичного трикутника існує ще одна формула, яка має назву формули синусів та наступне формулювання: у всякому сферичному трикутнику добуток синуса будь-якої сторони на синус прилеглого кута дорівнює добутку синусів протилежних елементів

Ця формула пов'язує між собою протилежні елементи трикутника – кути і сторони.

Доведення. Прирівнявши праві частини рівнянь (1.7) і (1.10), отримаємо рівняння (1.15), що й необхідно було довести. Аналогічно записують формулу для інших пар елементів трикутника (сторони і прилеглого кута):

sin b sin C sin c sin B,

sin c sin A sin a sin C.

Перегрупувавши члени в цих рівняннях, отримаємо

З останнього рівняння можна зробити висновок: у всякому сферичному трикутнику синуси сторін пропорційні синусам протилежних кутів і їхнє відношення є сталою величиною для даного трикутника. Формула синусів застосовується для обчислення одного з елементів, що входить у вказані рівняння, якщо відомі три інших.

15

Наступною формулою для розв’язання сферичного трикутника є

формула п'яти елементів, яка має формулювання: у всякому сферичному трикутнику синус будь-якої сторони, помножений на косинус прилеглого кута, дорівнює косинусу протилежної сторони цьому куту, помноженому на синус третьої сторони, мінус синус протилежної сторони цьому куту, помножений на косинус третьої сторони і на косинус кута, протилежного першій стороні

(1.16)

Ця формула пов'язує п'ять елементів сферичного трикутника – три сторони і два кути.

Доведення. Замінимо в рівнянні (1.13) літерні позначення рівняннями (1.6), (1.8), (1.11) і отримаємо рівняння (1.16), що й потрібно було довести. Для інших комбінацій кутів і сторін у сферичному трикутнику можна отримати ще п'ять аналогічних рівнянь.

Ще одною формулою для розв’язання сферичного трикутника є формула чотирьох елементів або формула котангенсів: у всякому сферичному трикутнику котангенс крайнього кута, помножений на синус середнього кута, дорівнює котангенсу крайньої сторони, помноженому на синус середньої сторони, мінус добуток косинусів середніх елементів (сторони і кута)

Ця формула пов'язує чотири поруч елементи сферичного трикутника, наприклад, елементи А, с, В, а (рис. 1.6). Назвемо два елементи цього трикутника – кут A і сторону a –крайніми елементами, а інші два елементи – сторону c і кут B – середніми елементами.

A

c

b

B

a C

Рис. 1.6. Суміжні елементи сферичного трикутника Доведення. Візьмемо формули (1.15) і (1.16) для одних і тих же сторін і

кутів у лівих частинах рівнянь, наприклад, для сторони b і кута A :

16

sin b sin A sin a sin B,

sin b cos A sin c cos a cos c sin a cos B.

Розділивши друге рівняння на перше, отримаємо:

ctgA sin c ctga cos c cos B , sin B

звідки отримаємо рівняння (1.17), що і необхідно було довести.

Аналогічно може бути написано ще п'ять таких рівнянь для інших поєднань чотирьох суміжних елементів. Формула котангенсів застосовується для обчислення сторони або кута трикутника, якщо вони лежать поруч з трьома відомими елементами.

Наступною формулою для розв’язання сферичного трикутника є формула косинуса кута із формулюванням: у всякому сферичному трикутнику косинус будь-якого кута дорівнює добутку косинусів двох інших кутів зі знаком «мінус» плюс добуток синусів тих же кутів на косинус сторони, прилеглої до них.

Ця формула пов'язує між собою три кути і одну зі сторін сферичного трикутника і приводиться тут без доведення.

У разі розв'язку прямокутних сферичних трикутників формули (1.14) – (1.18) стають одночленними, що прискорює обчислення. Для зручності запам'ятовування таких перетворених основних формул розв'язку прямокутних трикутників (рис. 1.7) існує наступне мнемонічне правило Непера-Модюі:

якщо катети прямокутного сферичного трикутника замінити їх доповненнями до 90° і не враховувати прямого кута, то косинус будь-якого шуканого елемента дорівнює добутку котангенсів суміжних з ним елементів, або добутку синусів несуміжних з ним елементів.

C

b

90°-b

a

A

Рис. 1.7. Прямокутний сферичний трикутник (до правила Непера-Модюі)

Наприклад,

Аналогічно, за формулами (1.21) – (1.24), користуючись мнемонічним правилом Непера-Модюі, можна встановити залежності для знаходження елементів B і c .

1.4. Розв’язок сферичних трикутників

Розв’язати сферичний трикутник – означає знайти його невідомі елементи за заданими відомими елементами. Для розв’язку сферичного трикутника загального вигляду (косокутного) необхідно і достатньо знати три будь-яких його елементи. У прямокутного сферичного трикутника один елемент – прямий кут завжди відомий, і для його розв’язку досить знати тільки два елементи. Ще до початку обчислень слід переконатися в дотриманні умов 1-7 (див. п. 1.2) між елементами трикутника. Розв’язок всякого сферичного трикутника складається з наступних операцій.

1.Виконати креслення з відповідними позначеннями. Вибрати формули, що зв'язують шуканий елемент із заданими. Необхідно, щоб шукані елементи знаходилися через задані, а не через знайдені в процесі розв’язку. При виборі формул слід віддавати перевагу обчисленню шуканих величин за тими функціями, які швидше змінюються. Малі кути точніше визначаються через синуси або тангенси, а кути, близькі до 90° – через косинуси або котангенси. Доцільніше виконувати розв’язок за функціями тангенса або котангенса, оскільки в цьому випадку є однозначною чверть шуканого аргументу. Невідомий елемент треба винести в ліву частину, перетворивши і спростивши вибрані формули.

2.Дослідити формули на знаки, тобто поставити над кожним множником

іу кожного члена правої частини рівняння знак, відповідний значенням аргументу і найменуванню функції. Потім визначити, в якій чверті розташований шуканий аргумент.

3.Скласти алгоритм розв’язку, загальний для всіх шуканих елементів у трикутнику. Порядок і розташування окремих дій в алгоритмі має дуже важливе значення при обчисленнях. Скорочується праця обчислювача, економиться до 30-50% робочого часу. Провести власне обчислення, враховуючи при цьому висновки аналізу формул на знаки. Обов'язково виконувати контроль.

Контрольні питання та приклади розв'язування задач до розділу 1.

18

Питання 1. Яким чином утворюється сферичний кут на поверхні сфери? Питання 2. Дати визначення великого та малого кіл сфери.

Питання 3. Дати визначення сферичного трикутника.

Питання 4. Навести межові обмеження щодо суми кутів сферичного трикутника.

Питання 5. За якими формулами розв’язують прямокутний сферичний трикутник?

Задача 1. Обчислити радіус малого кола з широтою 45°, паралельного великому колу з радіусом 6371,3 км.

Залежність між радіусами паралельних кіл виражається рівнянням (1.1), з розв'язання якого r = 4505,2 км.

Задача 2. Обчислити величину кута Р сферичного трикутника АРВ, якщо кут А дорівнює 62°, кут В – 58°, сферичний надлишок ε = 1°.

Сума кутів сферичного трикутника згідно формули (1.4) дорівнює 180°+ε, тому кут Р буде 61°.

Задача 3. Розв'язати сферичний трикутник АВС при відомих значеннях сторони АВ та кутів А і В.

Розв'язати сферичний трикутник – означає знайти його невідомі елементи за відомими. У даному прикладі невідомими елементами є сторони ВС і АС та кут С. Спочатку за формулою (1.18), записаної відносно кута С, знайдемо кут С. Скориставшись формулою (1.15) можна знайти сторони ВС і АС.

Задача 4. Розв'язати прямокутний сферичний трикутник АВС при відомих значеннях сторони АВ та кутів В і А=90°.

Поставлена задача у знаходженні сторін ВС і АС та кута С. За формулою (1.22) обчислюємо кут С. Для обчислення сторони ВС користуємося формулою (1.19), а сторони АС – (1.24).

19

Розділ 2 СИСТЕМИ НЕБЕСНИХ КООРДИНАТ

Системи небесних координат використовують в астрономії для опису положення світил на небі або точок на уявній небесній сфері. Координати світил або точок задаються двома кутовими величинами (або дугами), які однозначно визначають положення об'єктів на небесній сфері. Таким чином, системи небесних координат є сферичними системами координат, в яких перша координата — відстань — часто невідома і не відіграє ролі. Ці системи відрізняються одна від одної вибором основної площини та початку відліку на ній.

2.1. Допоміжна небесна сфера

Для визначення положення небесного світила σ використовують дві системи просторових координат: просторову прямокутну – з координатами X, Y, Z та полярну – з координатами α, β, R (рис. 2.1). Названі системи координат задовольняють основну вимогу до них – положення небесних світил необхідно знати як відносно Землі, так і взаємне їх відносне положення. Для названих систем координат початок координат розміщений в точці О, напрям осей можна задавати за вихідними даними використовуваної системи.

Рис. 2.1. Прямокутна просторова і полярна системи координат

В прямокутній просторовій системі координат положення світила σ визначається трьома лінійними координатами X, Y, Z. У цьому випадку відстань R від світила σ до точки О обчислюється за формулою

R 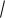X 2 Y 2 Z 2 . (2.1)

У полярній системі координат положення світила σ задається однією лінійною координатою – відстанню R = Oσ від світила σ до точки О і двома

20