Савчук підручник

Розділ 3. Розв'язування геодезичних задач

Отже, для встановлення геометричних зв’язків між трикутниками необхідно попередньо знайти величини всіх його елементів – кутів та сторін, тобто розв’язати. Враховуючи, що сторони в першокласних геодезичних мережах рідко перевищують 30 км, то трикутники тріангуляції вважаються

малими сфероїдними трикутниками. Саме такі трикутники ми і будемо в подальшому розглядати.

Можливість розв’язування малих сфероїдних трикутників як сферичних була розглянута в попередньому розділі (див. п.2.7.3).

Сферичний надлишок

Із сферичної тригонометрії відомо, що сферичний

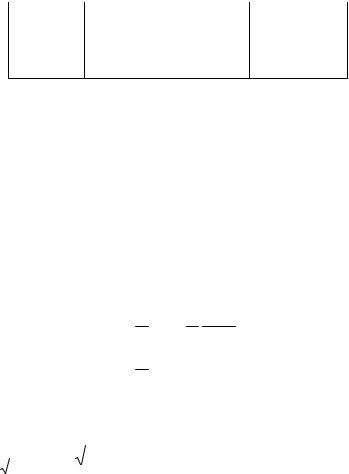
надлишок A B C 1800 сферичного трикутника ABC (рис.3.2) рівний площі цього трикутника, якщо радіус сфери, на

Рис. 3.2

92

Розділ 3. Розв'язування геодезичних задач

2cos 2aR

Вмалих сфероїдних трикутниках s R і P R , тому

тригонометричні функції малих аргументів можна розкласти в ряди із збереженням тільки перших членів розкладів:

У випадку вимірювання всіх кутів ці формули можна перетворити так, щоб сферичний надлишок був функцією лише однієї сторони

93

Розділ 3. Розв'язування геодезичних задач

В першокласних геодезичних мережах сферичний надлишок обчислюється з точністю до 0.001".

Для обчислення сферичного надлишку в кожному трикутнику, крім кутів, повинні бути відомі також довжини сторін. Вияснимо, з якою точністю повинні бути відомі довжини сторін і кути, щоб обчислений за ними сферичний надлишок мав похибку не більше 0.001".

Для рівностороннього трикутника на основі формул (3.4) можемо записати

малого сферичного трикутника (табл. 3.1). В табл. 3.1 приведено також можливі значення сферичного надлишку для рівносторонніх трикутників.

Одним із основних застосувань сферичного надлишку є виявлення нев’язки у трикутнику тріангуляції

94

Розділ 3. Розв'язування геодезичних задач

Способи розв’язування малих сфероїдних трикутників

а) за формулами сферичної тригонометрії

Розв’язування малих сфероїдних трикутників, як було вже зазначено, зводиться до розв'язування сферичних трикутників за формулами сферичної тригонометрії. Так для трикутника ABC (рис. 3.2) при заданій стороні a та кутах A,B,C , на основі формули синусів, запишемо

де радіус сфери R визначається як функція середньої широти B, на якій розташований трикутник, за відомими формулами

Недоліком даного способу є те, що сторони трикутника виражаються в частинах радіуса, а також необхідність визначати тригонометричні функції малих кутів з досить високою точністю (10-12 розрядів).

95

Розділ 3. Розв'язування геодезичних задач

б) за теоремою Лежандра

Теорема Лежандра для малих сферичних трикутників:

якщо сторони плоского і сферичного трикутників відповідно рівні між собою, то кути плоского трикутника рівні кутам сферичного трикутника, зменшеними на одну третину сферичного надлишку.

Нехай ABC - сферичний, а A'B'C' - плоский трикутник, сторони якого рівні відповідним сторонам сферичного трикутника (рис. 3.3). Такий трикутник носить назву лежандровий трикутник.

BB

A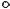 b C A b C

Рис.3.3

Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде

96

Розділ 3. Розв'язування геодезичних задач

Сферичний надлишок можна обчислити, наприклад, за формулами (3.4).

Отже, якщо у сферичному трикутнику ABC відома вихідна сторона, наприклад, c і сферичні кути A,B,C (див. рис.3.3), то за першою формулою (3.4) обчислюємо сферичний надлишок трикутника і знаходимо плоскі кути A',B',C'.

Потім розв’язуємо трикутник за стороною c та знайденими плоскими кутами, застосовуючи формули плоскої тригонометрії (теорему синусів), тобто

b c sin B',

Точність розв'язування сферичних трикутників, які можна розв’язувати за теоремою Лежандра, залежить не тільки від розмірів сторін, але і від форми трикутника. Аналізом формул встановлено, що допустимі розміри сторін трикутника знаходяться в межах від 75 до 150 км.

в) за способом аддитаментів

У попередньому способі для застосування формул плоскої тригонометрії вводилися поправки за сферичність у кути.

Можливим є також спосіб використання сферичних кутів, але з введенням поправок в сторони трикутника. Розглянемо даний спосіб.

Із сферичного трикутника ABC (рис.3.3) за теоремою синусів маємо

97

Розділ 3. Розв'язування геодезичних задач

де c- відома сторона, b - шукана сторона даного сферичного трикутника.

Поскільки сторони сферичного трикутника є малими в порівнянні з радіусом сфери R, то їх тригонометричні функції розкладемо в ряд, обмежуючись членами третього порядку:

Позначивши

і, крім того

c'sinsin BA b',

Або остаточно

і, аналогічно, для другої сторони

98

Розділ 3. Розв'язування геодезичних задач

З цих формул видно, що головні члени представляють собою розв'язування сферичного трикутника як плоского, причому кути в них є сферичними. Поправочні члени

сферичного трикутника за формулами (3.10), (3.11) називають способом аддитаментів. Строго кажучи, аддитаментами називалися малі поправки до логарифму головного члена, коли формули виводились із застосуванням логарифмів. Хоча логарифмічні методи втратили своє значення і на практиці не застосовуються, проте в назвах окремих способів, і в тому числі при розв’язуванні сферичних трикутників, збереглися первісні терміни.

Отже, якщо від вихідної сторони відняти її аддитамент і розв’язати трикутник зі сферичними кутами за формулами плоскої тригонометрії, то, додавши до знайдених довжин сторін їхні аддитаменти, отримаємо довжини сторін сферичного трикутника.

Точність розв’язування малих сферичних трикутників способом аддитаментів є аналогічною, як і для розв’язування їх за теоремою Лежандра.

г) за виміряними сторонами

У випадку, коли в геодезичній мережі вимірюються лише сторони трикутників, виникає потреба обчислення горизонтальних кутів, які в подальшому можуть мати окреме застосування, наприклад, для передачі геодезичного азимута від однієї сторони до іншої.

Порядок обчислень при цьому буде наступний. Виміряні між пунктами прямолінійні відстані редукують на поверхню еліпсоїда, згідно теорії редукцій геодезичних вимірювань з фізичної поверхні Землі на поверхню еліпсоїда.

За знайденими таким чином сторонами a,b,c сферичного трикутника ABC обчислюють плоскі кути

99

Розділ 3. Розв'язування геодезичних задач

A',B',C' (див. рис.3.3), використовуючи наступні формули плоскої тригонометрії:

Якщо довжини сторін не перевищують 100 км, то достатньо обчислити сферичний надлишок за формулами (3.2), а потім одну третину його додати до кожного плоского кута A',B',C' згідно формули (3.7).

100

Розділ 3. Розв'язування геодезичних задач

3.4.2. Розв’язування головних геодезичних задач

а) на поверхні сфери

Використання сфери вигідно, в першу чергу, для наближеного розв’язування головних геодезичних задач - прямої та оберненої.

Введемо наступні позначення координат на сфері

(рис.3.4):

- географічна широта;- географічна довгота;

- азимут дуги великого кола;- сферична відстань (довжина дуги великого кола, виражена в

s

частинах радіуса сфери , R ).

P

Рис.3.4

Пряма геодезична задача Нехай задані географічні координати 1, 1 деякої точки

Q1 (рис. 3.4б), а також полярні координати і 1 другої точки Q2. Вимагається за цими даними знайти географічні координати2, 2 точки Q2 і азимут 2 з другої точки на першу. Таким чином, пряма геодезична задача полягає в перетворенні полярних координат в географічні (сферичні).

101